1. Матричний спосіб розв’язання

Через те, що , то для матриціА існує обернена матриця й

. (1.7)

Помноживши обидві частини рівняння ліворуч на матрицю, одержимо Оскільки й, то .

Відшукання розв’язку системи (1.6) за формулою (1.7) називають матричним способом розв’язання даної системи.

2. Формули Крамера (Крамер Г. ( 1704-1752) – швейцарський математик)

Формули

(1.8)

називаються формулами Крамера, де – визначник, отриманий з визначника заміною i-го стовпця стовпцем вільних членів.

Доведення.

Для доведення матричну рівність (1.7) запишемо у вигляді

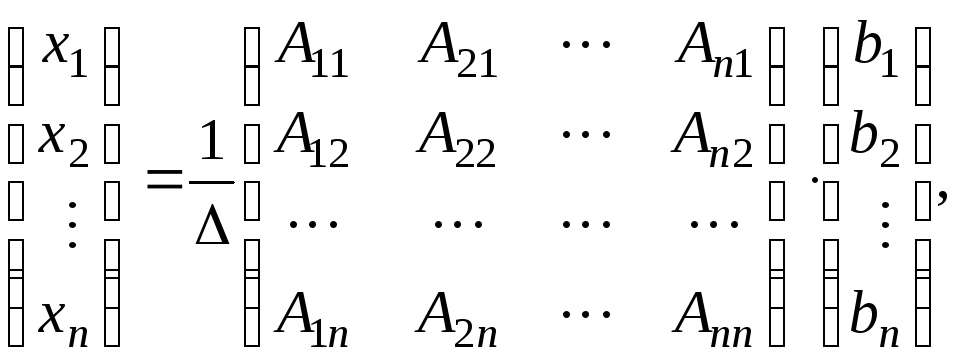
тобто

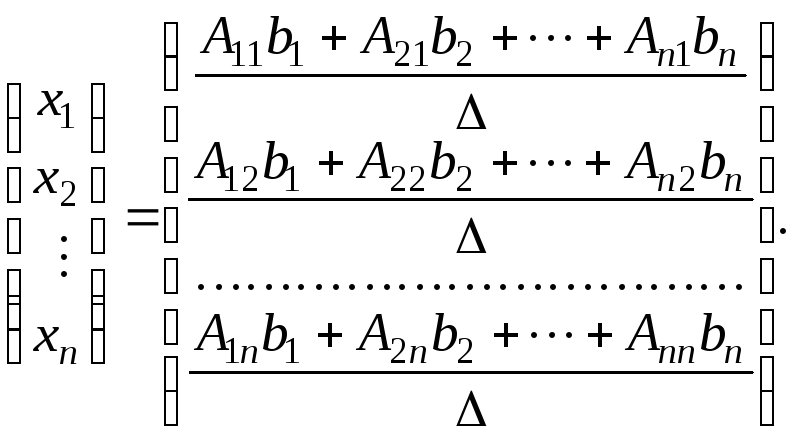
Звідси маємо, що

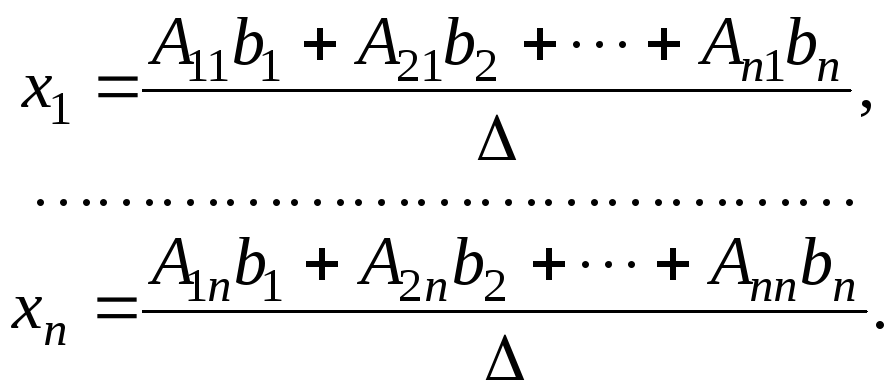
Але є розкладанням визначника

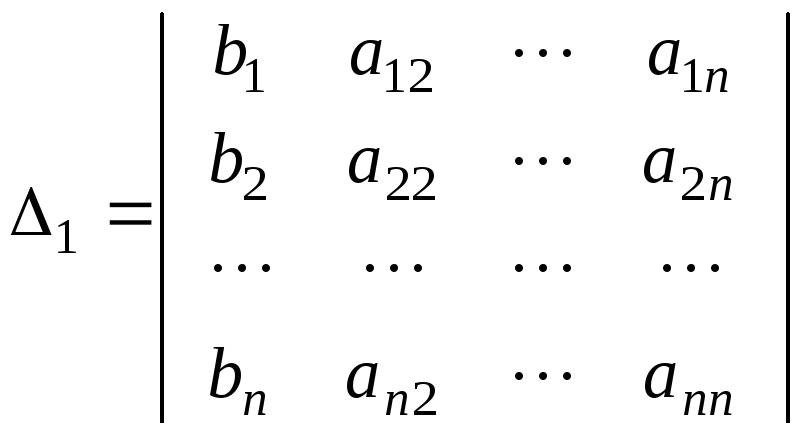за елементами першого стовпця. Визначник виходить із визначниказаміною першого стовпця коефіцієнтів стовпцем з вільних членів.

Отже, .

Аналогічно можна показати, що , деотримано зшляхом заміни другого стовпця коефіцієнтів стовпцем з вільних членів і т.д.:

.

Теорему доведено.

Приклад.

Розв’язати систему 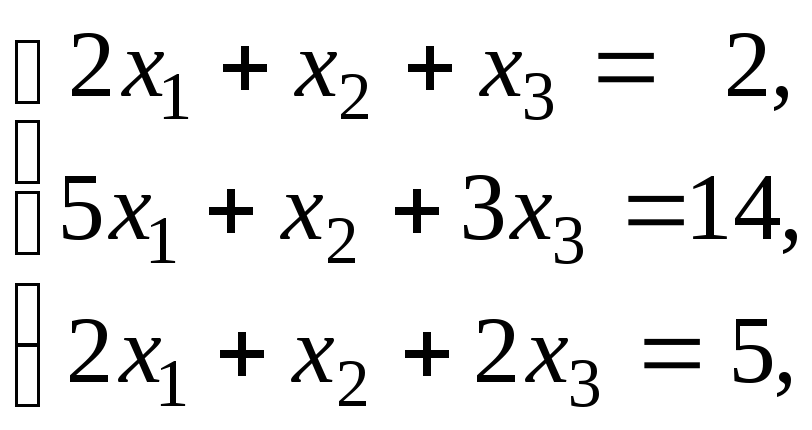двома методами: 1) матричним способом; 2) за формулами Крамера.

Розв’язання.

1. У матричному вигляді система має вигляд , де

, ,.

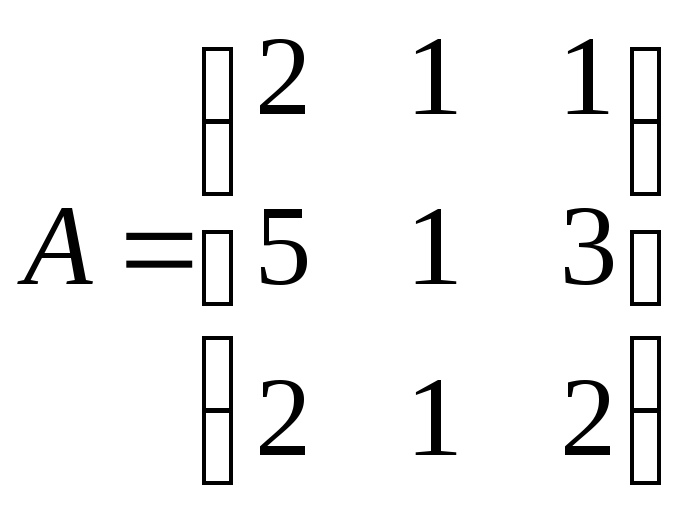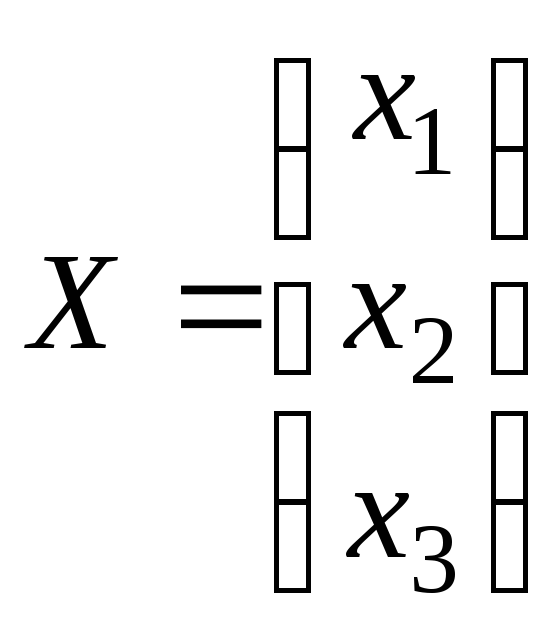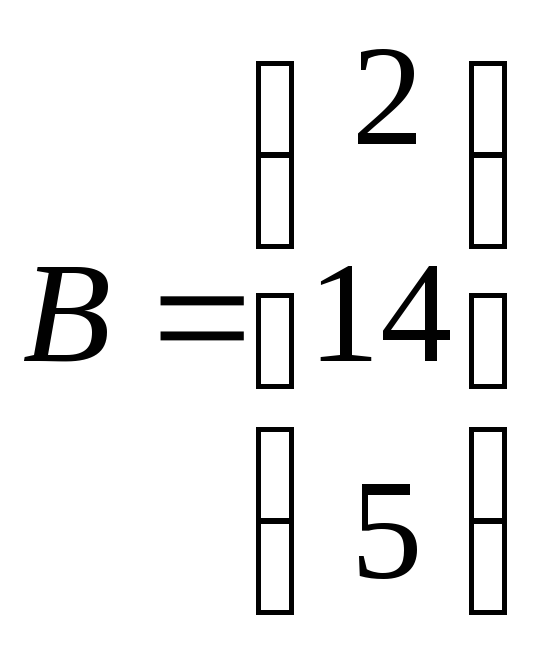З матричного рівняння . Розв’язання матричним методом можливо, якщо матрицяА є невиродженою, тобто при :

,

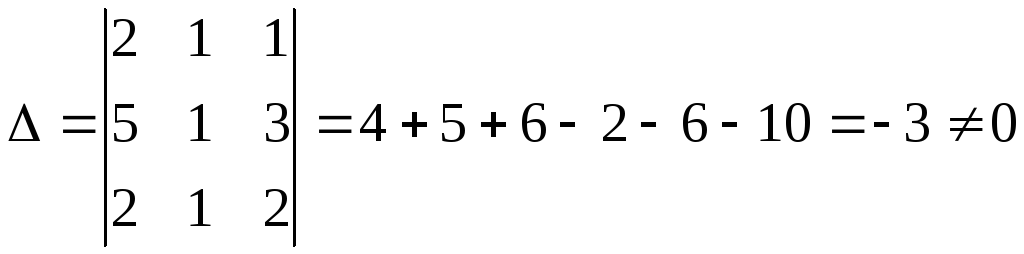тобто обернена матриця існує.

Знайдемо обернену матрицю :

.

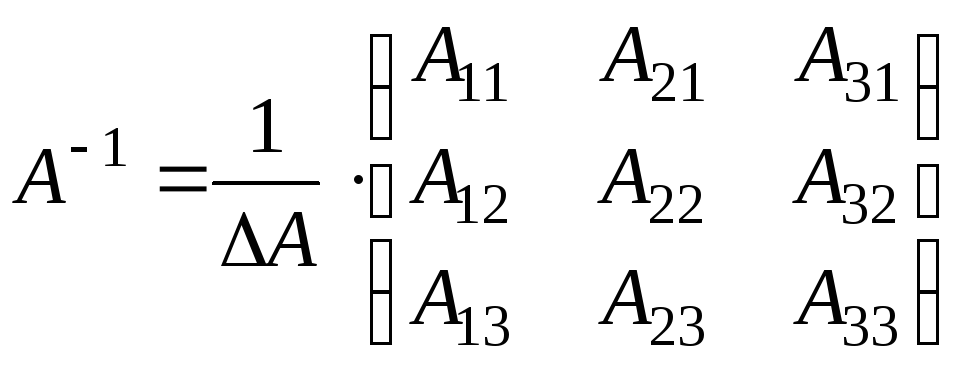Обчислимо алгебраїчні доповнення:

; ;;

; ;;

; ;;

.

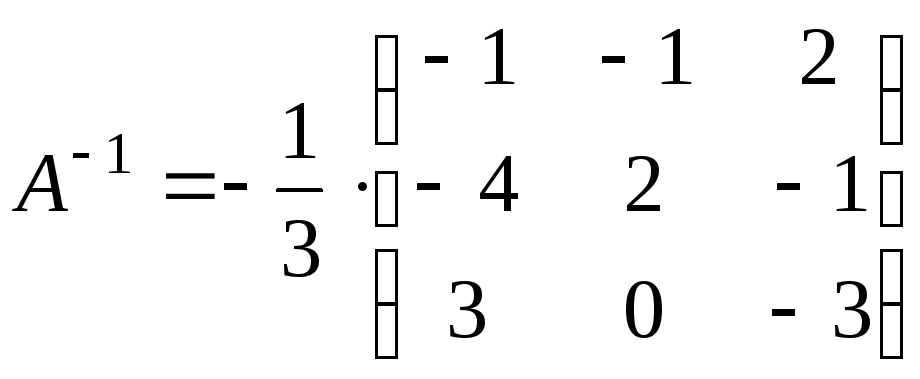Тоді .

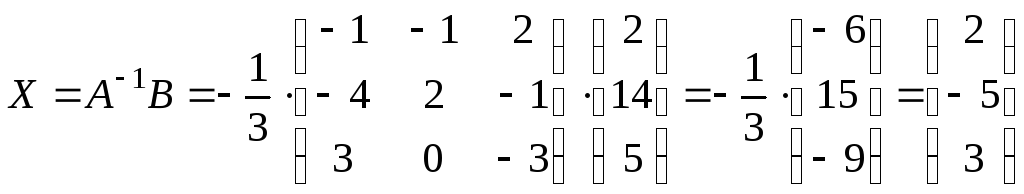Таким чином ,,.

2. За формулами Крамера

, ,.

Визначник системи знайшли в попередньому пункті:. Обчислимо,:

;

;

.

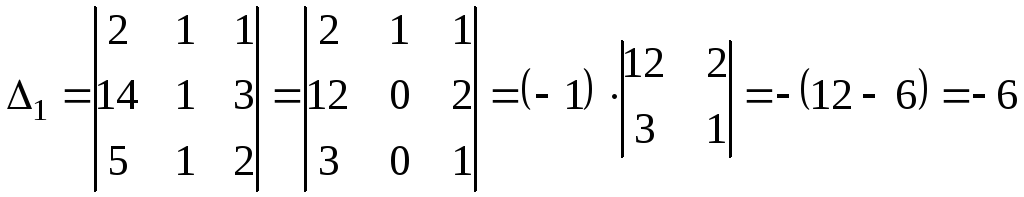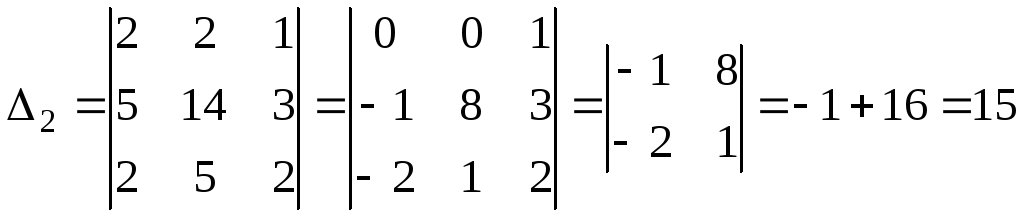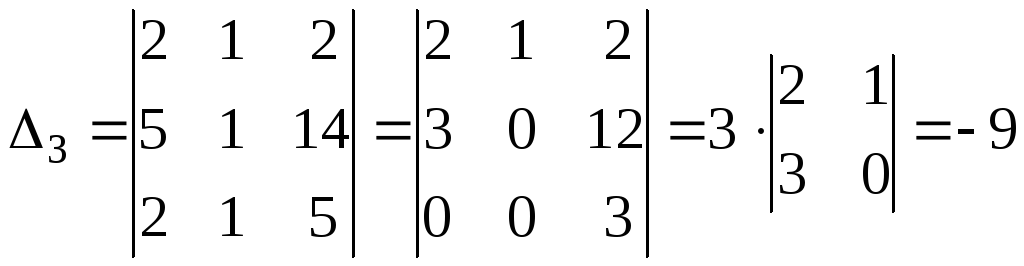Тоді ,,.

Правила практичного знаходження всіх розв’язків сумісної системи лінійних рівнянь випливають із наслідків теореми.

Алгоритм розв’язання довільної системи лінійних рівнянь

1. Знайти ранги основної й розширеної матриць системи. Якщо , то система несумісна.

2. Якщо , то система сумісна. Виділяють базисний мінор порядку (нагадування: мінор, порядок якого визначає ранг матриці, називається базисним). Невідомі, коефіцієнти за яких становлять базисний мінор, називаютьбазисними, а інші (п – ) невідомих називають вільними.

3. Дану систему замінюють рівносильною їй системою, що складається з тих рівнянь, у які ввійшли елементи базисного мінору (інші рівняння відкинути). Базисні невідомі залишають ліворуч, а вільні переносять у праві частини рівнянь.

4. Якщо число базисних невідомих дорівнює числу невідомих системи, то система має єдиний розв’язок, і його знаходять або матричним способом, або за формулами Крамера.

5. Якщо число базисних невідомих не дорівнює числу невідомих системи, то система має незліченну множину розв’язків. Із системи, отриманої на кроці 3, знаходять вираження базисних невідомих через вільні. Надаючи вільним невідомим довільні значення, одержимо загальний розв’язок системи. Розв’язок, що виходить із загального при конкретних значеннях вільних невідомих, називається частинним розв’язком.

Приклад.

Дослідити на сумісність та розв’язати системи:

1) 2)

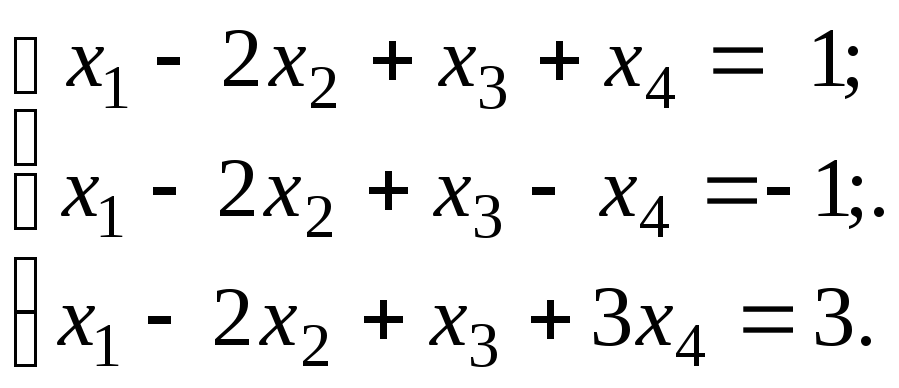
Розв’язання.

1)

через те, що .

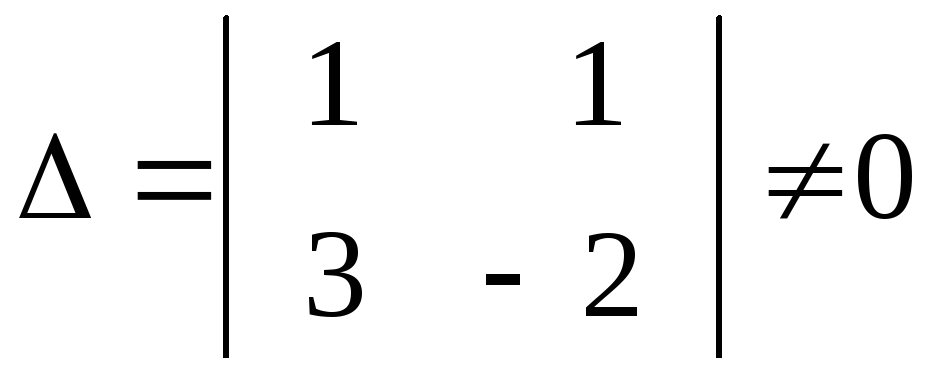Таким чином, , отже, система несумісна.

2)

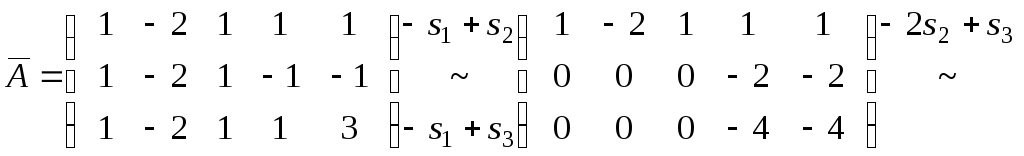
Через те, що , то система сумісна і базисних невідомих буде 2. Беремо два перших рівняння:

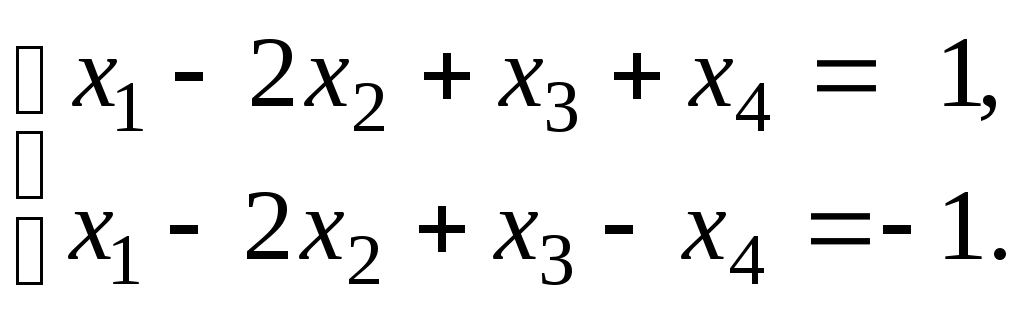
Виразимо базисні невідомі тачерез вільніта:

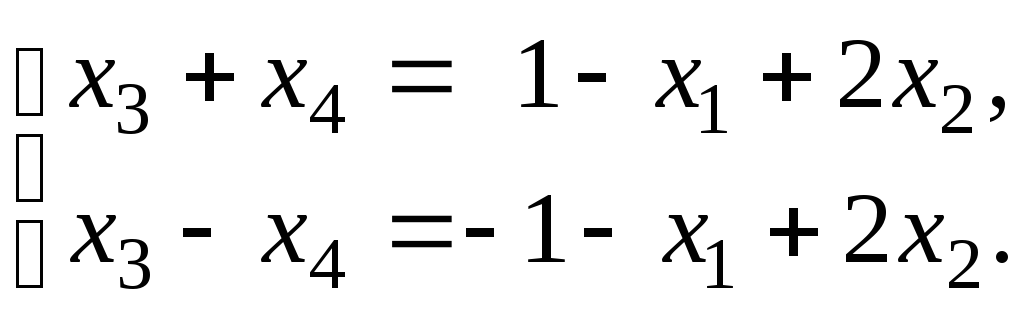
Використовуючи формули Крамера, маємо

, .

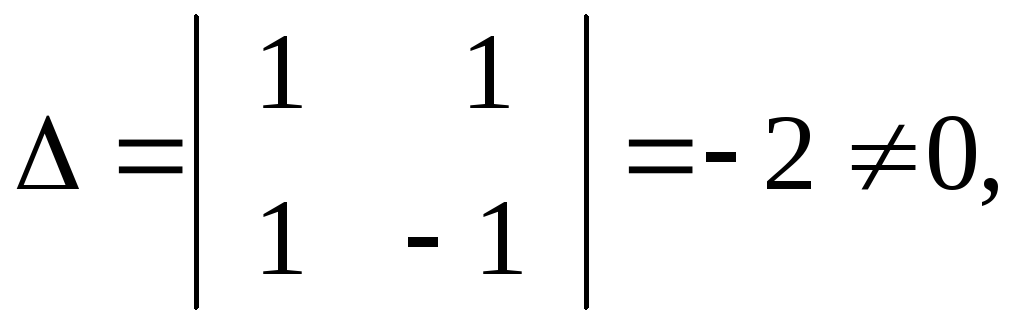
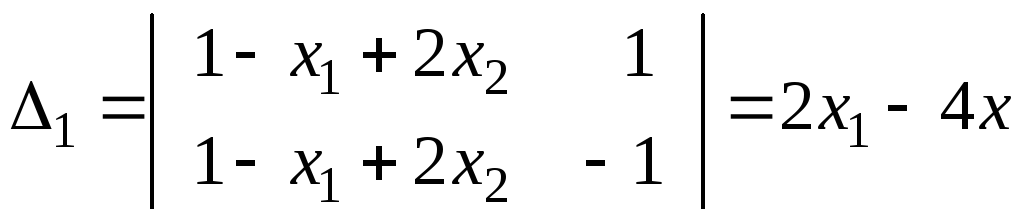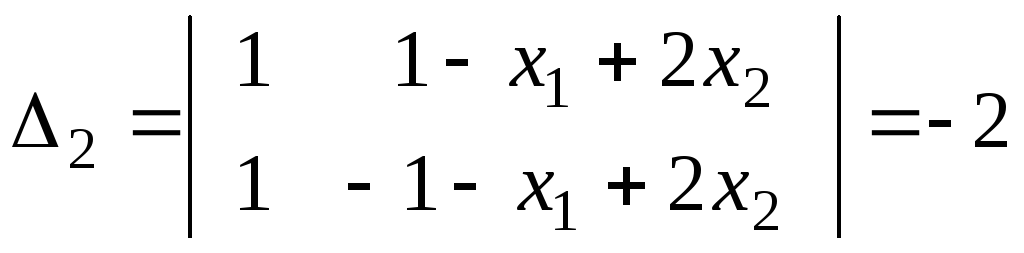Отже, ,– загальнийрозв’язок. Нехай, наприклад, отримаємо один з часткових розв’язків:

Контрольні запитання та завдання

1. Дайте визначення сумісної і несумісної, означеної і неозначеної системи алгебраїчних лінійних рівнянь.

2. Запишіть систему рівнянь у матричній формі.

3. Сформулюйте теорему Кронекера-Капеллі.

4. В чому полягає матричний спосіб розв’язання системи алгебраїчних рівнянь?

5. Дайте виведення формул Крамера.

6. Наведіть алгоритм розв’язання системи алгебраїчних рівнянь.

7. Які невідомі називають «вільними»?

8. Скільки базисних невідомих має система?

9. Скільки вільних невідомих має система?