1.4 Ранг матриці

Основні поняття

Нехай задана матриця А розмірністю

Виділимо в ній k рядків і k стовпців (, де – менше із чисел та).Мінором k-го порядку цієї матриці називається визначник k-го порядку, складений з елементів, що стоять на перетині виділених k рядків і k стовпців. (Зазначимо, що таких мінорів можна скласти штук, де– число сполучень ізп елементів по k).

Найбільший з порядків мінорів даної матриці, відмінних від нуля, називається рангом матриці. Позначається або.

Очевидно, що .

Приклад.

Знайти ранг матриці .

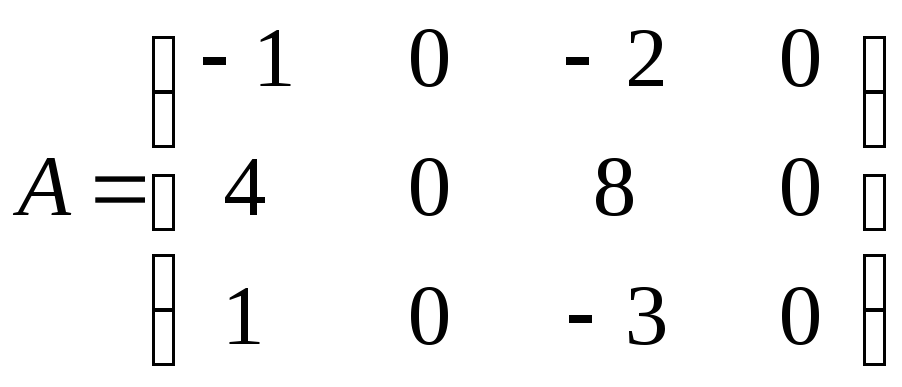Розв’язання.

Всі мінори 3-го порядку дорівнюють нулю. Є мінор 2-го порядку, відмінний від нуля 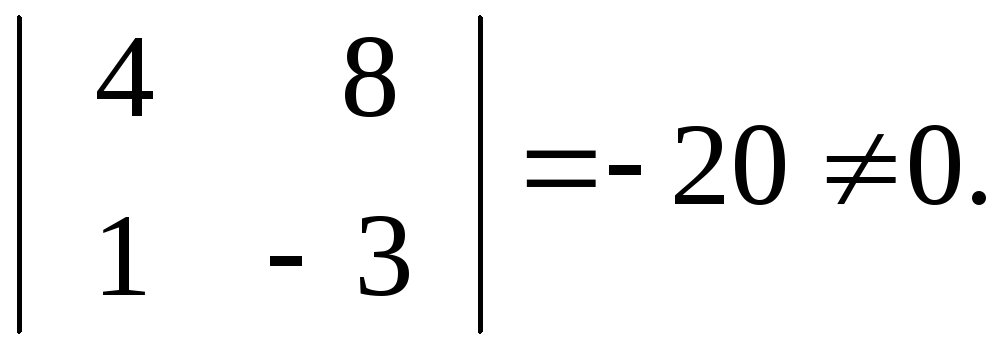Отже,.

Приклад.

Знайти ранг матриці .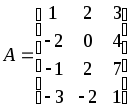

Розв’язання.

Всі мінори третього порядку цієї матриці відрізнятимуться різним набором рядків. Кількість таких наборів дорівнює числу сполучень із чотирьох по три: .Таким чином, це будуть мінори:

,,

,.

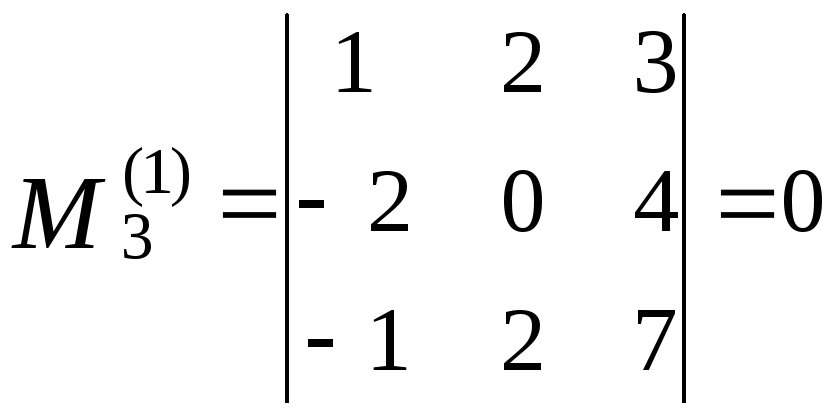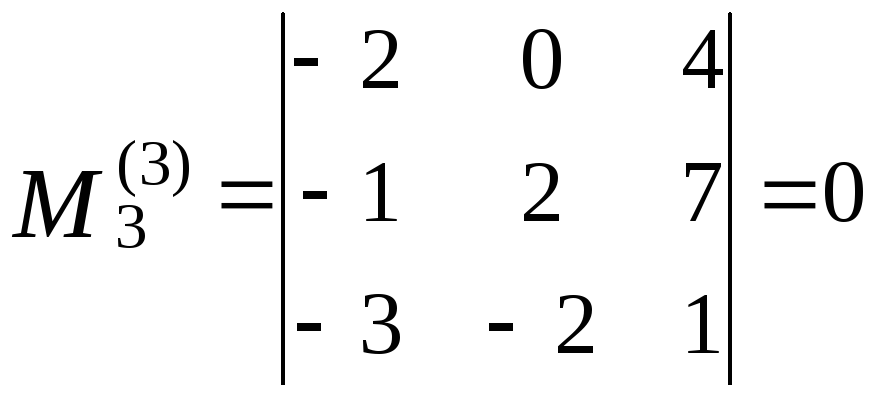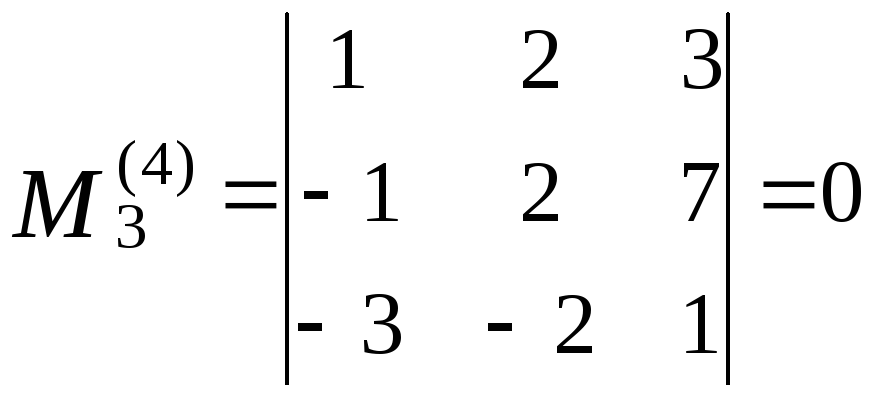З того, що всі вони дорівнюють нулю, випливає, що ранг матриці менше 3. Серед мінорів другого порядку маємо:

.

Таким чином, .

Елементарні перетворення матриці.

Під елементарними перетвореннями матриці розумітимемо:

– транспонування матриці;

– множення будь-якого рядка (стовпця) матриці на будь-яке число, відмінне від нуля;

– додавання до будь-якого рядка (стовпця) будь-якого рядка (стовпця), яке помножено на будь-яке число;

– перестановка місцями будь-яких рядків (стовпців).

Для практики особливе значення має наступна теорема про інваріантність (незмінність) рангу матриці при її елементарних перетвореннях.

Теорема. Елементарні перетворення не міняють рангу матриці.

Доведення.

При будь-якому елементарному перетворенні визначник або не змінює свого значення, або змінює знак, всі нульові мінори матриці залишатимуться нульовими. Всі ненульові мінори при будь-яких елементарних перетвореннях залишаються ненульовими. Отже, ранг не зміниться.

Слід зауважити, що власне матриця, як таблиця чисел, змінюється.

Теорему доведено.

Дві матриці А і В називаються еквівалентними, якщо одна з них виходить із іншої за допомогою елементарних перетворень. Позначається А ~ В.

За допомогою елементарних перетворень будь-яку матрицю можна привести до матриці східчастого вигляду. Кількість ненульових рядків (ненульовий той, у якому хоча б один елемент є відмінним від нуля) матриці східчастого вигляду дорівнює рангу матриці.

Приклад.

Знайти ранг матриці .

Розв’язання.

Виконуючи елементарні перетворення, одержуємо

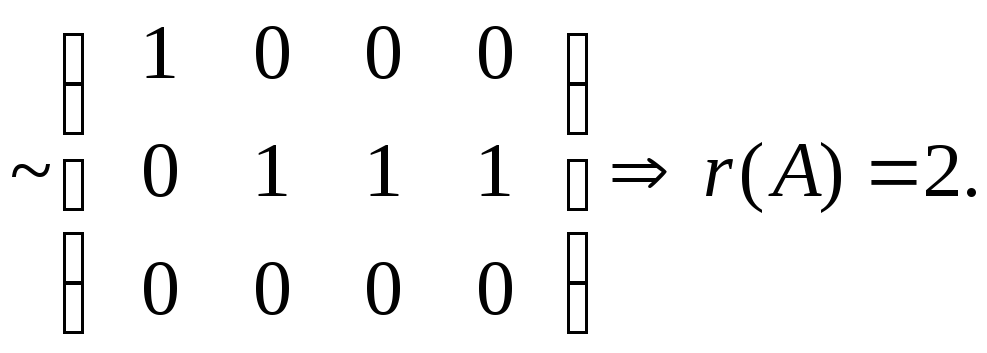
Знаходження оберненої матриці за допомогою елементарних перетворень

Невироджена матриця шляхом елементарних перетворень тільки над стовпцями або рядками приводиться до одиничної матриці. Наступна теорема дає спосіб знаходження оберненої матриці за допомогою елементарних перетворень одиничної матриці.

Теорема. Якщо до одиничної матриці порядку n застосувати ті ж перетворення тільки над стовпцями (рядками) і в тому ж порядку, за допомогою яких невироджена матриця А порядку n приводиться до одиничного, то отримана матриця буде обернена до матриці А.

Доведення.

Нехай А – невироджена матриця. Здійснимо над стовпцями (рядками) матриці А елементарні перетворення, що приводять її до одиничної матриці. Ті ж перетворення й у тому ж порядку здійснимо над матрицею Е. Якщо при цьому матриця Е перейде в матрицю В , то матриця А перейде в матрицю , звідки.

Теорему доведено.

При цьому матриці А і Е записують поруч, тобто для даної матриці А nn-го порядку побудуємо прямокутну матрицю розміру. Використовуючи елементарні перетворення над рядками або стовпцями, приводимо матрицюдо вигляду, що завжди можливо, оскількиА невироджена. Тоді .

Приклад.

За допомогою елементарних перетворень знайти матрицю , обернену матриці

.

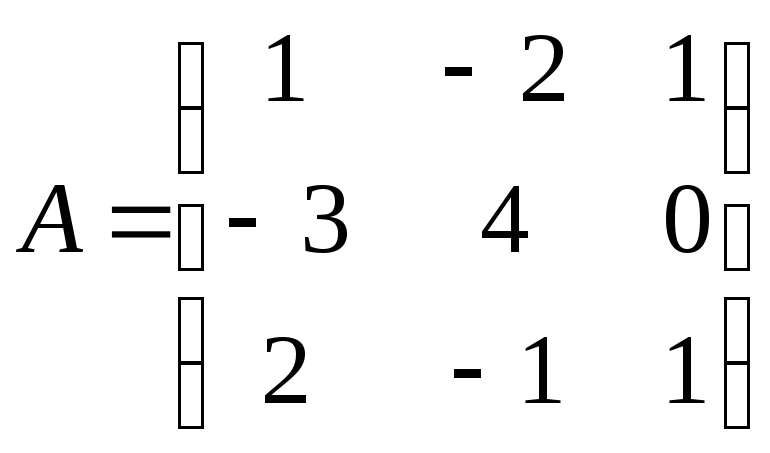Розв’язання.

Побудуємо матрицю і проведемо над нею елементарні перетворення.

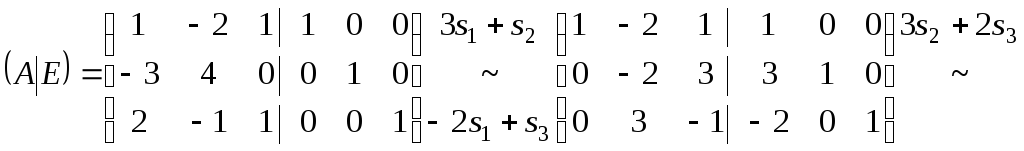
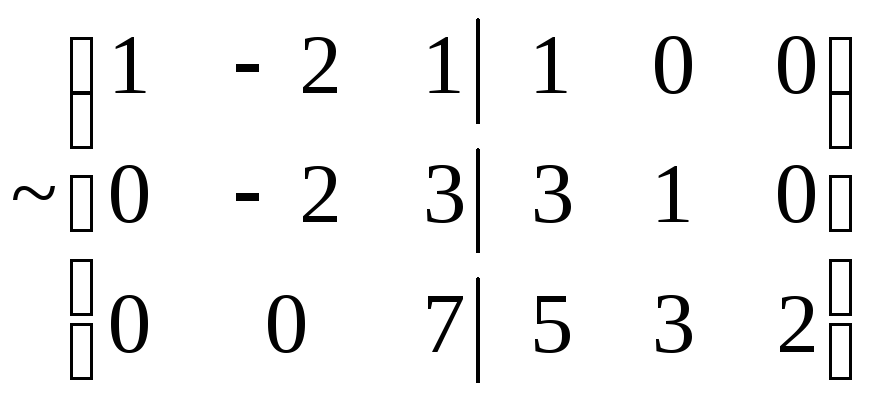
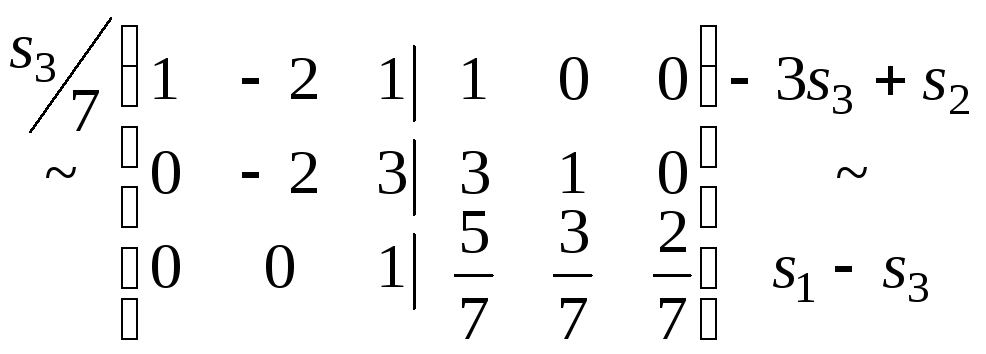
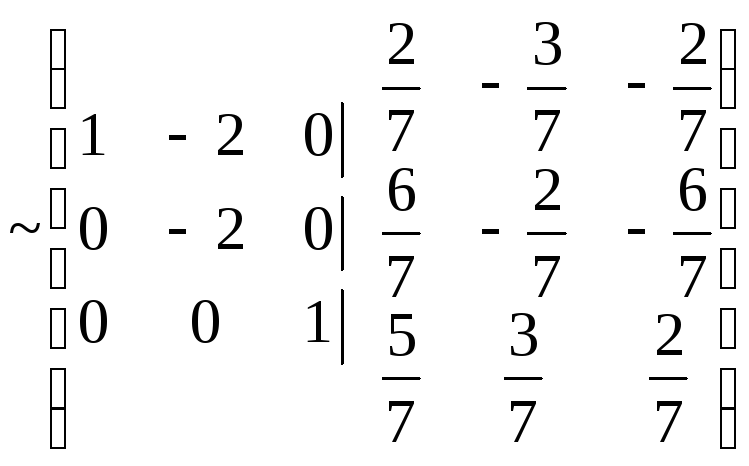
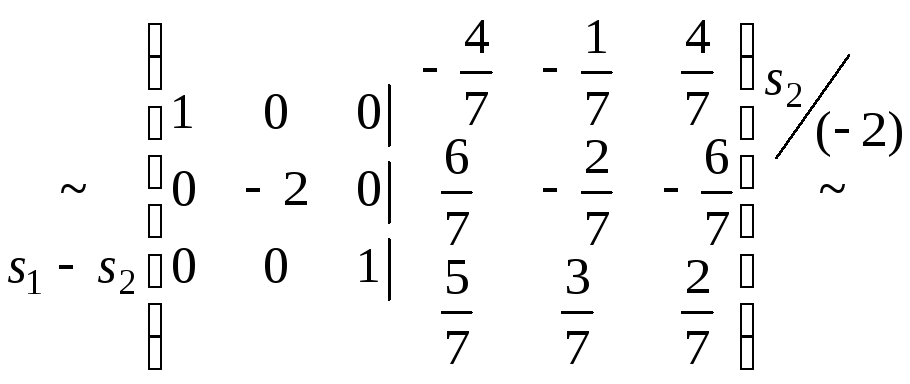
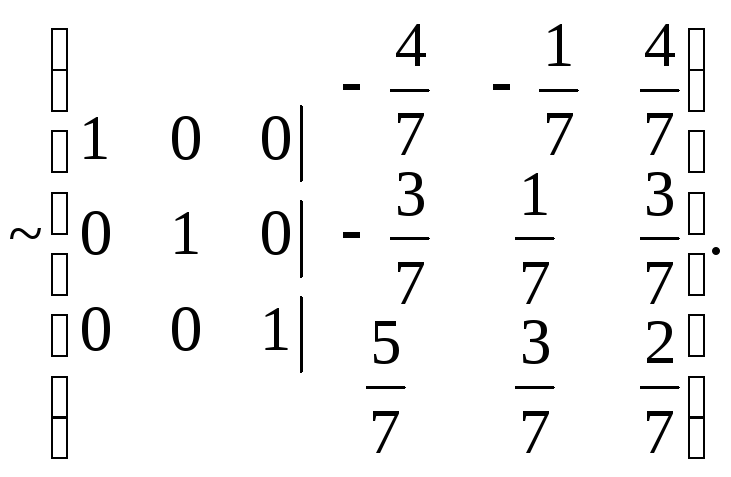Тоді

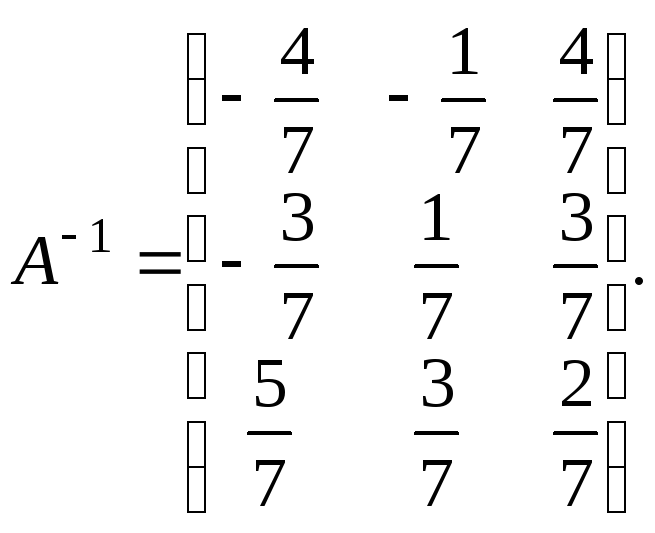
Базисний мінор

Говоритимемо, що k-й рядок матрицілінійно виражається через -рядки, якщо існують числа, не рівні нулю одночасно, що(отримана рівність указує на те, щоk-й рядок є лінійною комбінацією рядків )

Рядки називаютьсялінійно залежними, якщо існують числа не рівні нулю одночасно, що їхня лінійна комбінація дорівнює нулю, тобто.

Якщо не існує таких чисел або рівністьмає місце тільки при , то рядки називаютьсялінійно незалежними.

Базисним мінором матриці називається мінор, порядок якого дорівнює рангу матриці.

Мінор порядку називаєтьсябазисним, якщо він відмінний від нуля, а всі мінори -го порядку дорівнюють нулю.

Зауваження.

У матриці може бути кілька базисних мінорів.

Рядки й стовпці, на перетину яких стоїть базисний мінор, називаються базисними.

Теорема. (Теорема про базисний мінор). Базисні рядки матриці лінійно незалежні. Всі інші рядки лінійно виражаються через базисні.

Доведення.

1. Розглянемо матрицю . Нехай базисний мінорперебуває у верхньому лівому куті, якщо це не так, то за допомогою елементарних перетворень можна добитися такого його положення. Покажемо, що базисні рядки є лінійно незалежними.

Доведемо від протилежного. Припустимо, що деякий рядок, наприклад , лінійно виражається через перші рядки, тобто існують числане рівні нулю одночасно, що. Віднімемо зr-того рядка матриці перший рядок, помножений на , потім другий, помножений най т.д. до. Тоді в базисному мінорірядокбуде нульовий, тобто. Але базисний мінормає бути відмінним від нуля. Отримане протиріччя вказує на те, що наше припущення про лінійну залежність першихрядків є неправильним.

2. Додамо будь-який рядок з тих, що не ввійшли до базисних, і будь-який стовпець. Одержимо мінор порядку, який, відповідно до означення рангу матриці, дорівнює нулю: .

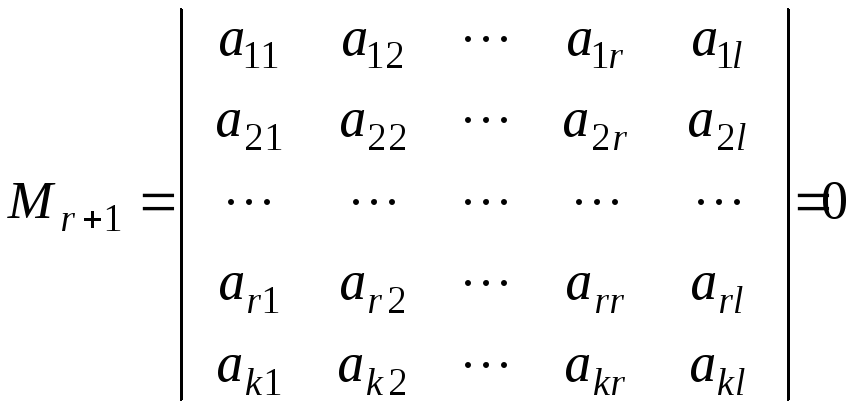Нехай а.

Розкладемо мінор за елементами останнього стовпця

Звідси одержуємо формулу , де, яка свідчить, що елементиk-го рядка лінійно виражаються через базисні рядки.

Теорему доведено.

Наслідки.

1. Максимальна кількість лінійно незалежних стовпців, дорівнює максимальній кількості лінійно незалежних рядків.

2. Визначник квадратної матриці дорівнює нулю, тоді й тільки тоді, коли його рядки (стовпці) лінійно залежні.

3. (Визначення рангу матриці). Ранг матриці дорівнює кількості лінійно незалежних рядків (стовпців).

Приклад.

Довести, що рядки

, ,

лінійно незалежні.

Розв’язання.

Побудуємо з них матрицю і знайдемо її ранг.

Через те, що r(A)=3, то всі рядки матриці А лінійно незалежні, а, отже, лінійно незалежні і задані рядки.

Приклад.

Довести, що рядки ,,,лінійно залежні.

Розв’язання.

Побудуємо матрицю з цих рядків і знайдемо її ранг.

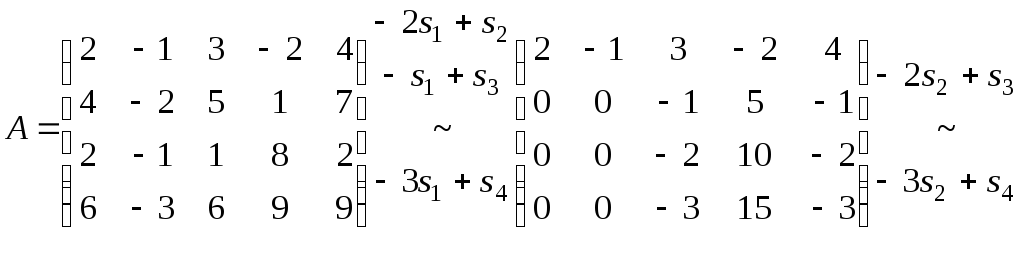
Через те, що ранг матриці дорівнює двом, r(A)=2, то всі її рядки лінійно залежні, а, отже, лінійно залежні і задані рядки.

Метод обвідних мінорів

Мінор порядку називаєтьсяобвідним мінором , якщо він містить у собі всі елементи. Нехай знайдений мінор порядкувідмінний від нуля. Розглядатимемо всі мінори-го порядку, що містять у собі (обвідні) мінор. Якщо всі мінори-го порядку дорівнюють нулю, то ранг дорівнює, якщо знайдеться хоча б один мінор відмінний від нуля, то вся процедура повторюється.

Приклад.

Знайти ранг матриці .

Розв’язання.

Серед елементів матриці А є відмінні від нуля, наприклад елемент, що стоїть у лівому верхньому куті. Серед мінорів, обвідних цей елемент, також є відмінні від нуля, наприклад

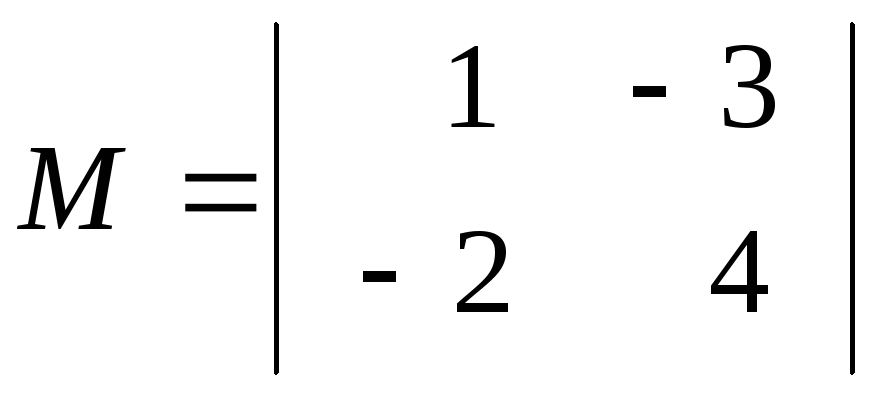. Серед мінорів, обвідних , тобто серед мінорів,

, ,,,

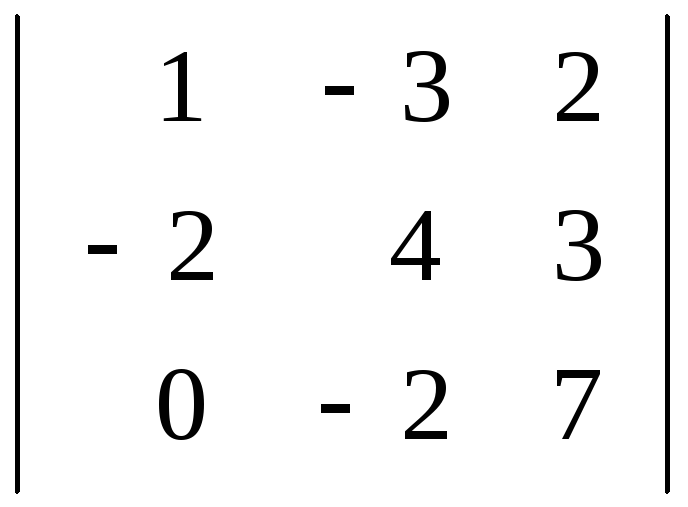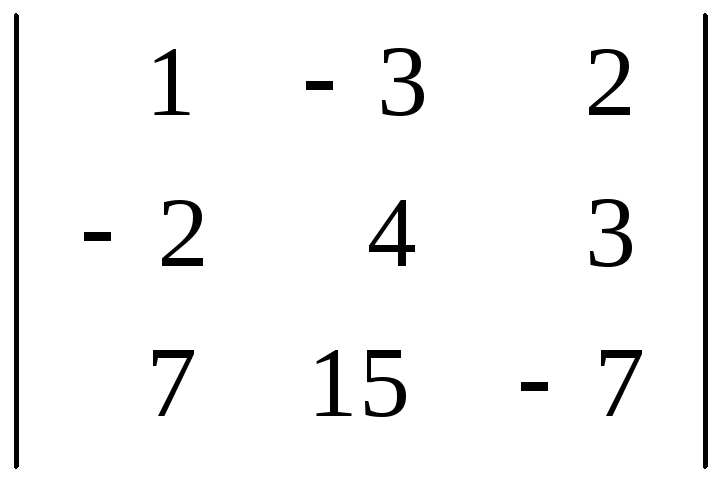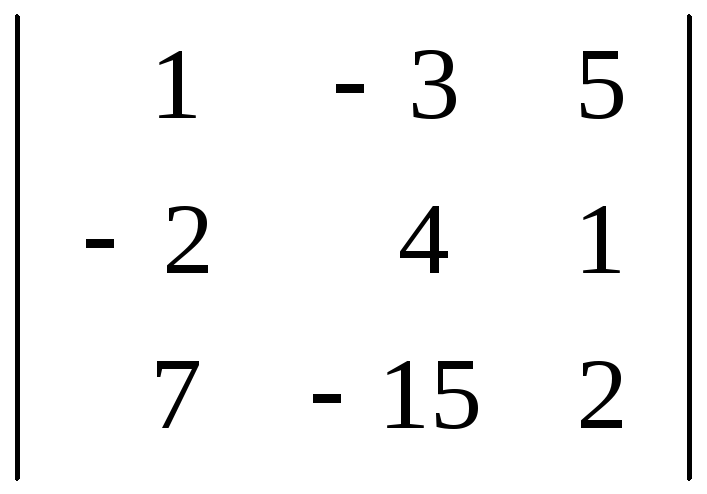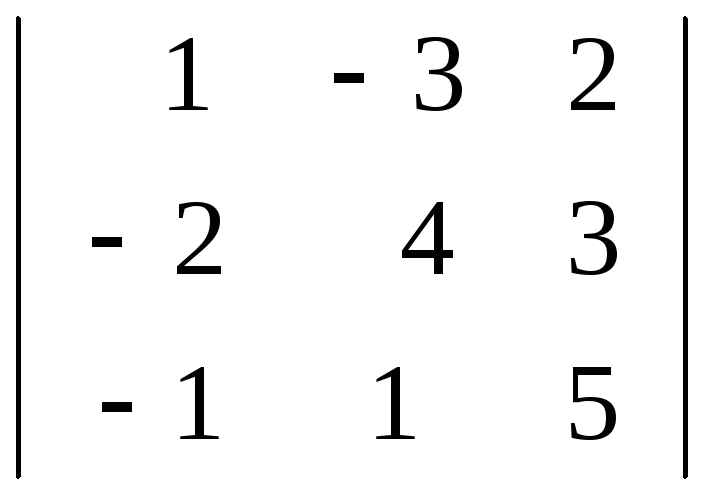немає відмінних від нуля. Отже, ранг матриці А дорівнює двом.

Контрольні запитання та завдання

1. Дайте означення мінору матриці. Чому дорівнює максимальний порядок мінору?

2. Дайте означення рангу матриці.

3. Перерахуйте елементарні перетворення матриці.

4. Обґрунтуйте незмінність рангу матриці при елементарних перетвореннях.

5. Сформулюйте теорему про базисний мінор матриці.

6. Наведіть алгоритм побудови оберненої матриці за допомогою елементарних перетворень.