1.3 Обернена матриця

Основні поняття

Нехай А – квадратна матриця n-го порядку

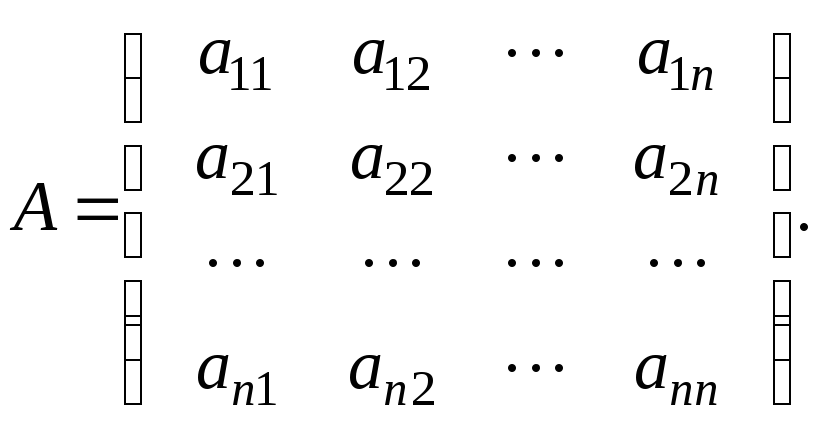
Матрицею, союзною або приєднаною до матриці А, називається матриця

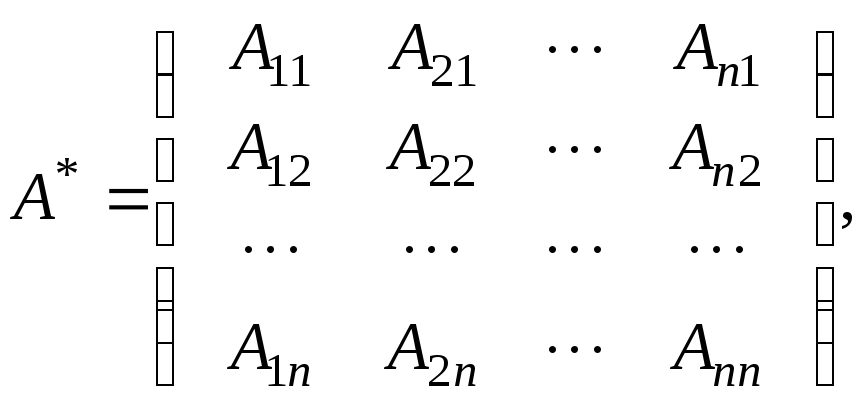
де – алгебраїчне доповнення елемента даної матриціА (воно визначається так само, як і алгебраїчне доповнення елемента визначника).

Теорема. Якщо А – квадратна матриця та – союзна до неї, то .

Доведення.

Проведемо доведення для випадку матриці 3-го порядку.

Хай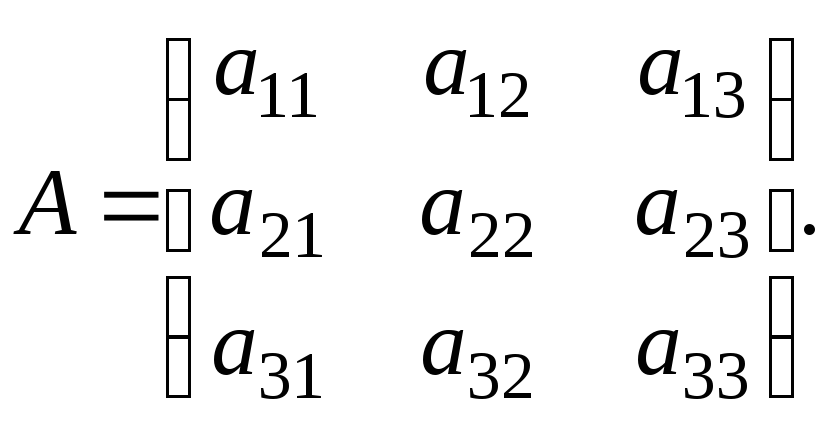Складемо союзну матрицюі знайдемо добуток матрицьА і :

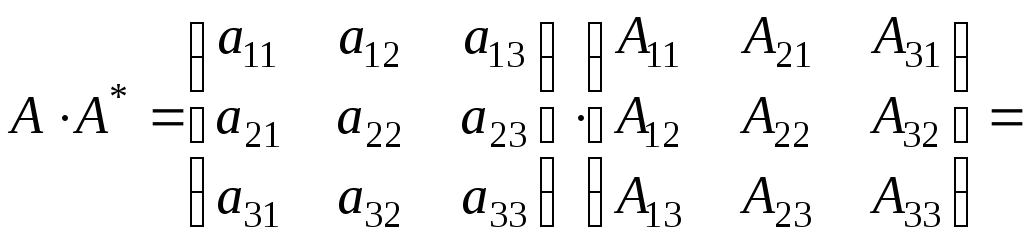
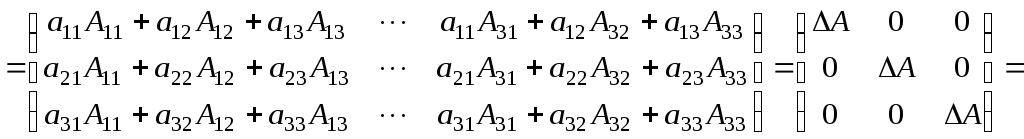
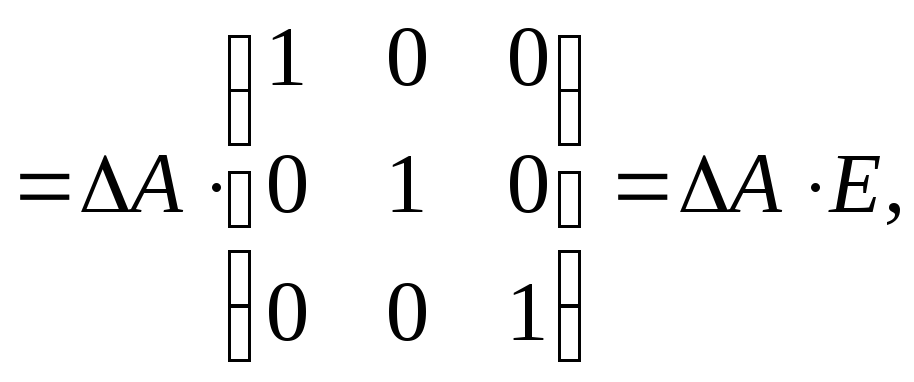тобто . Аналогічно переконуємося, щоПри доказі використовували властивості9 і 10 визначників.

Теорему доведено.

Матриця називаєтьсяоберненою до матриці А, якщо

де Е – одинична матриця того ж порядку, що й матриця А. Матриця має ті ж розміри, що й матрицяА.

Квадратна матриця А називається невиродженою, якщо визначник не дорівнює нулю:. У протилежному випадкуматрицяА називається виродженою.

Теорема. Для того, щоб квадратна матриця А мала обернену

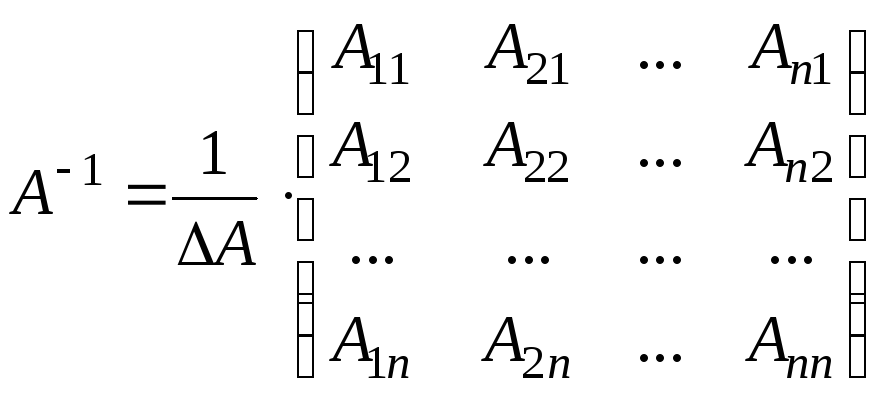, необхідно й достатньо, щоб матриця А була невиродженою.

Доведення.

Необхідність. Нехай для матриці А існує обернена до неї , тобто. Покажемо, що.

З огляду на те, що визначник добутку квадратних матриць одного порядку дорівнює добутку визначників матриць, що перемножуються (), то. Оскільки, то.

Достатність. Нехай . Покажемо, що матриця є оберненою до А. Оскільки й, тойПорівнюючиотримані результати з означенням оберненої матриці одержуємо

тобто

Теорему доведено.

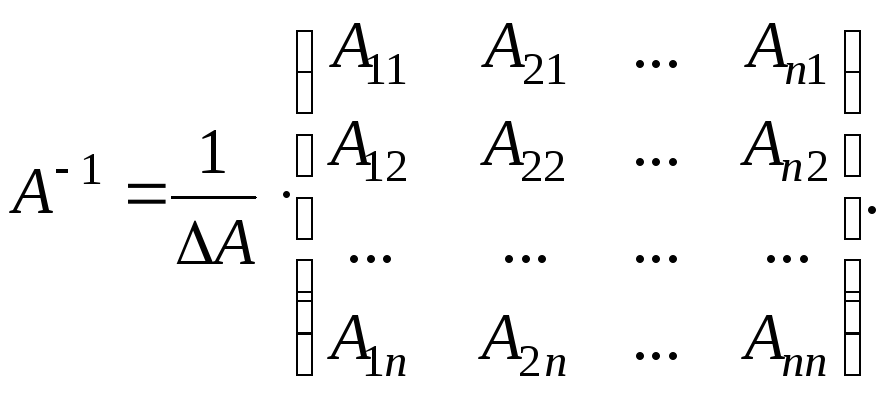
Для обернена матриця має вигляд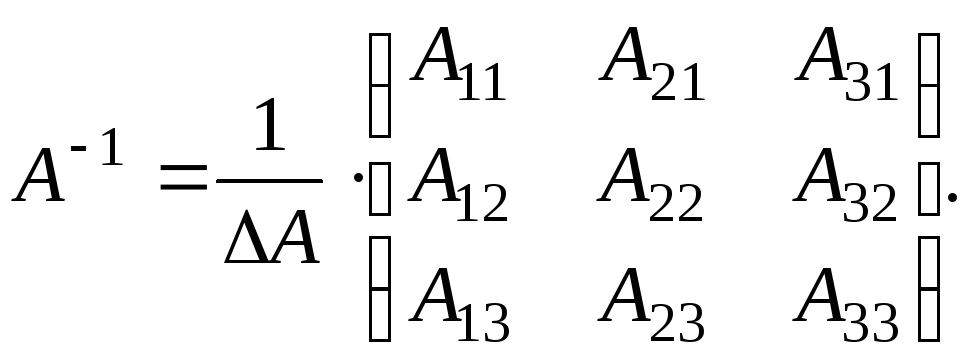

Властивості оберненої матриці

.

.

.

.

Приклад.

Знайти , якщо

Розв’язання.

1. Обчислимо визначник

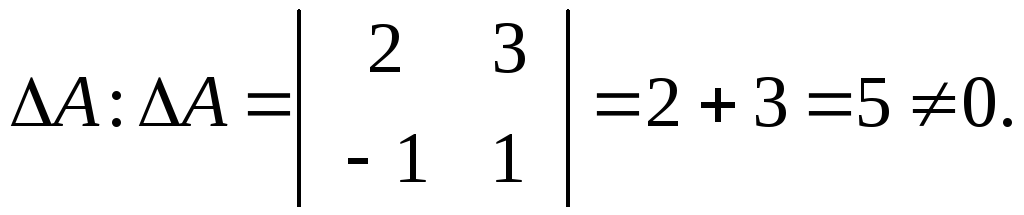
2. Знайдемо союзну матрицю , ,,,

тому .

3. Знаходимо

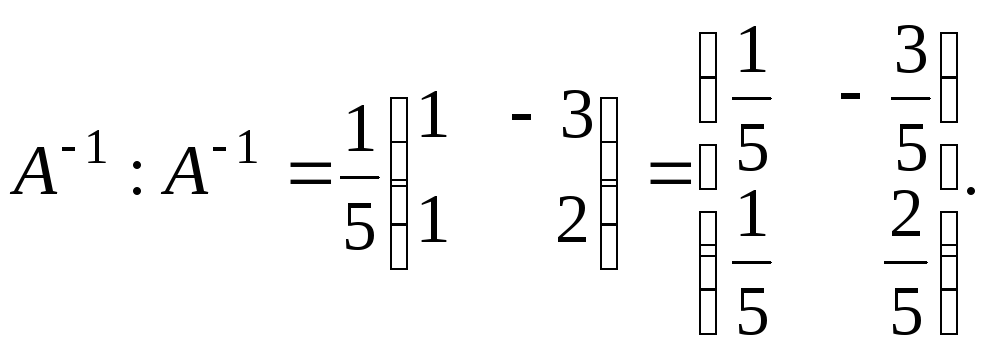
Перевірка:

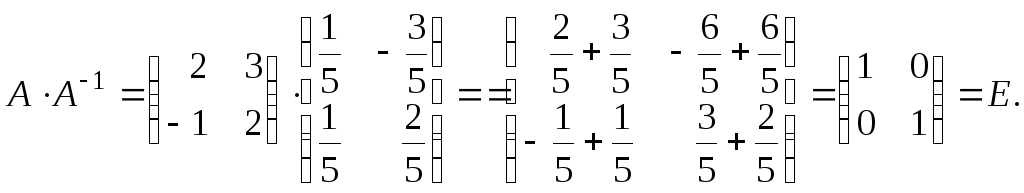
Приклад.

Визначити, при яких значеннях існує матриця, обернена до матриці

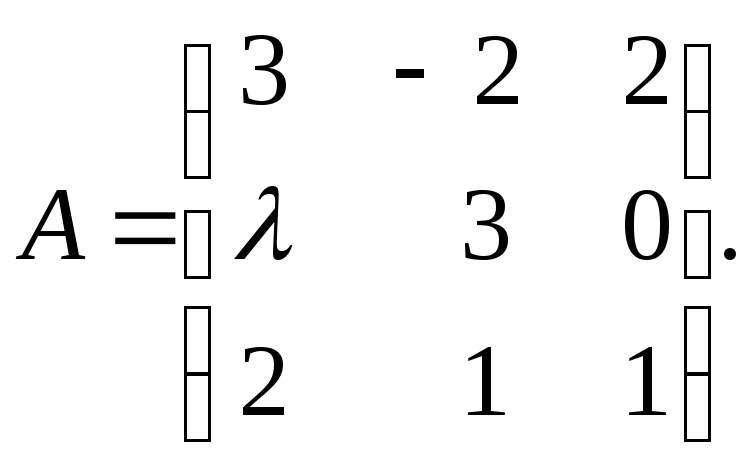
Розв’язання.

Будь-яка невироджена матриця має обернену. Знайдемо визначник матриці А:

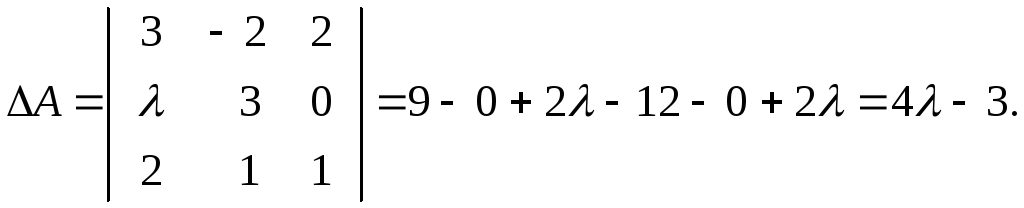
Якщо , тобто, то, тобто матрицяА невироджена та має обернену.

Приклад.

Показати, що матриця А є оберненою до В, якщо

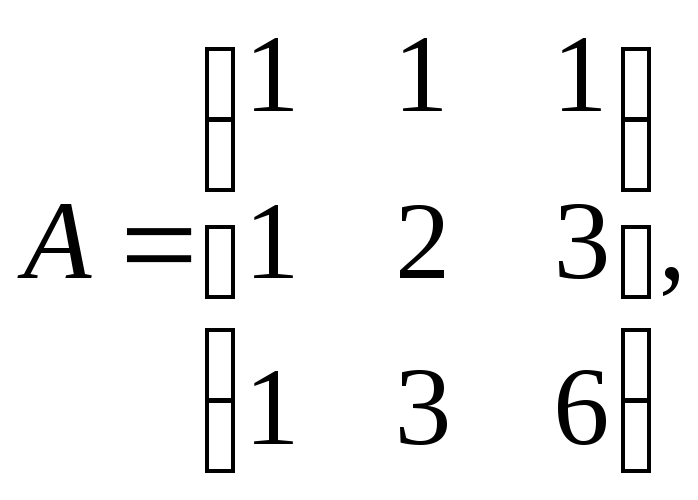
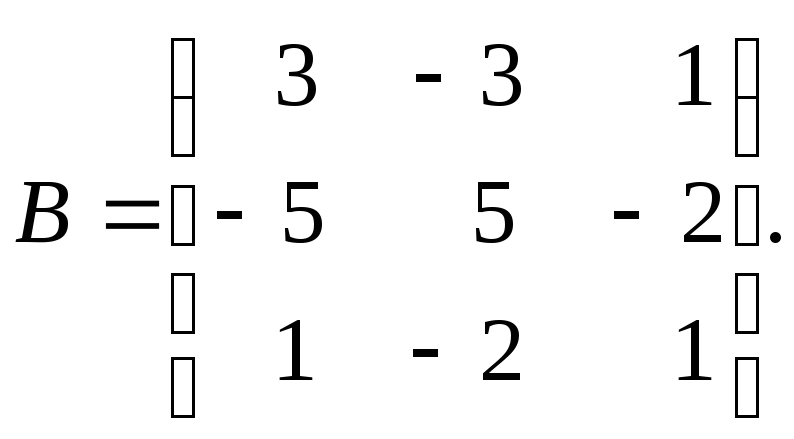
Розв’язання.

Знайдемо добуток матриць А і В:

.

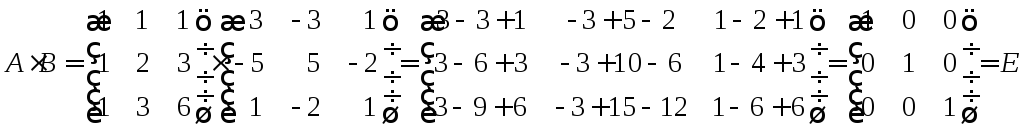Аналогічно . Отже за означенням матриця А є оберненою для В.

Матриці спеціального виду

Якщо матриця дійсна, то вона називається:

– ортогональною, якщо або ;

– симетричною, якщо ;

– кососиметричною, якщо .

Зауваження.

У кососиметричній матриці на головній діагоналі знаходяться нулі.

Нехай – комплексна матриця, де – комплексні числа (– для будь-яких ). Якщо,– дійсні матриці, то , деА – дійсна, а В – комплексна частини матриці С.

Матриця називаєтьсякомплексно-спряженою до матриці С.

Матриця називаєтьсяспряженою до матриці С.

Якщо матриця комплексна, то вона називається:

– ермітовою, якщо ;

– косоермітовою, якщо ;

– унітарною, якщо або.

Зауваження.

1. В ермітовій матриці на головній діагоналі стоять дійсні числа.

2. У косоермітовій матриці на головній діагоналі стоять чисто уявні числа.

Приклад.

Довести, що матриця є ортогональною.

Розв’язання.

.

Через те, що , то матрицяА – ортогональна.

Приклад.

Показати, що матриця 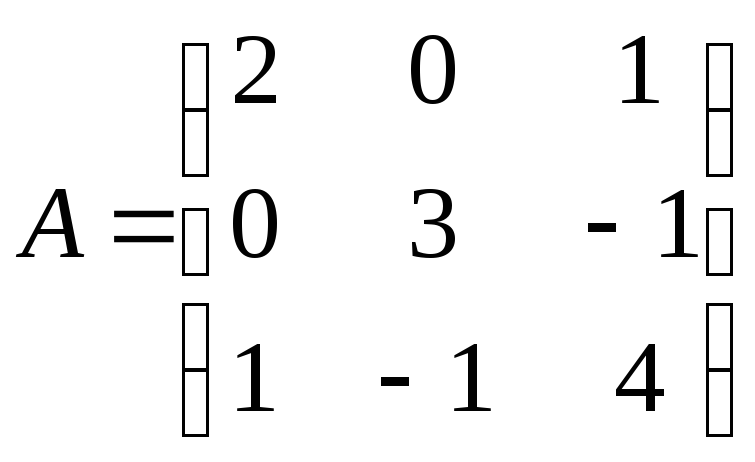є симетричною.

Розв’язання.

Через те, що 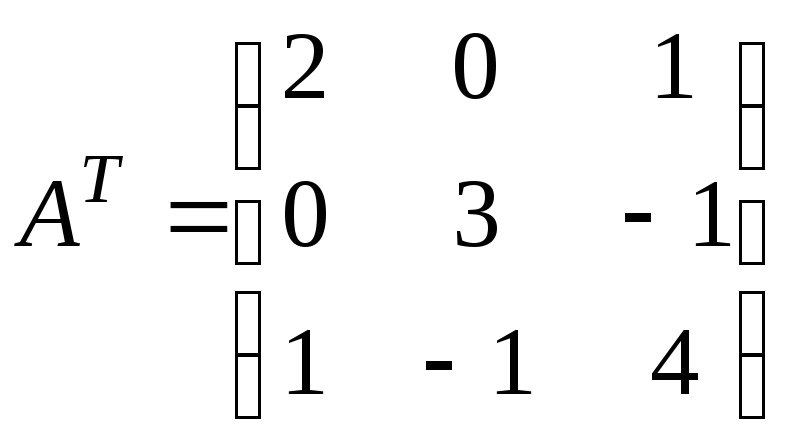і, то матрицяА є симетричною.

Контрольні запитання та завдання

1. Дайте визначення союзної або приєднаної матриці.

2. Яка матриця відсутня у рівності ?

3. Дайте визначення оберненої матриці.

4. Наведіть формулу, за якою знаходиться обернена матриця.

5. Для якої матриці існують обернена матриця?

6. Наведіть алгоритм побудови оберненої матриці.

7. Сформулюйте властивості обернених матриць.