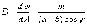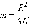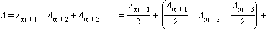Дифракция Френеля на круглом отверстии

Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r₀. Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке Pприблизительно гасят друг друга.

При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.

Можно показать, что радиус зоны Френеля с номером m при не очень больших m:

.

Расстояние "a" примерно равно расстоянию от источника до преграды, расстояние "b" - от преграды до точки наблюдения P.

Если отверстие оставляет открытым целое число зон Френеля, то, приравняв r₀ и r_m, получим формулу для подсчета числа открытых зон Френеля:

.

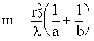При m четном в точке P будет минимум интенсивности, при нечетном - максимум.

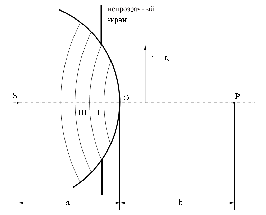
Дифракция Френеля от диска

      Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис. 9.4).   Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

      Парадоксальное, на первый взгляд, заключение, в силу которого в самом центре геометрической тени может находиться светлая точка, было выдвинуто Пуассоном в 1818 г. и впоследствии было названо его именем. «Пятно Пуассона» подтверждает правильность теории Френеля.

5.Зоны Френеля. Дифракция Френеля на круглом отверстии и непрозрачном диске.

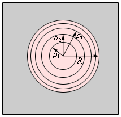
Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки Pдолжны отличается на половину длины волны, т. е.  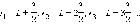Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).

Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия

 радиусы ρ_m зон Френеля: 

Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R: 

Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол αмежду лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно: 

A1 > A2 > A3 > ... > A1,

где A_m – амплитуда колебаний, вызванных m-й зоной. суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна 

или A = A_m + 1 / 2, так как выражения, стоящие в скобках, равны нулю. Если диск закрывает зоны не слишком больших номеров, то A_m + 1 ≈ 2A₀ и A ≈ A₀, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.

6. Дифракция Фраунгофера. Дифракция на щели. Дифракционная решетка.

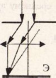
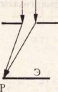
Дифракция Фраунгофера В случае дифракции Фраунгофера рассматривается падение на препятствие плоской волны (бесконечно удаленный источник света) и подразумевается, что зона наблюдения удалена от препятствия на достаточно большое расстояние (находится на бесконечности). Коротко говоря, это “дифракция в параллельных лучах”.

Различают два случая дифракции света - дифракция Френеля - или дифрак­ция в сходящихся лучах и дифракция Фраунгофера - дифракция в параллельных лучах. В первом случае на препятствие падает плоская (или сферическая волна), а дифракционная картина наблюдается на экране, находящемся на конечном рас­стоянии от щели (рис. 8.24). Во втором случае на щель падает плоская волна, а ди­фракционная картина наблюдается на эк­ране, находящемся в фокальной плоскости собирающей линзы, установленной между щелью и экраном (рис. 8.24).

.

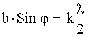При четном числе зон Френеля k = 2m, где m = ±1, ±2... все зоны можно разбить на соседние пары, которые гасят друг друга . Следовательно условие минимума при дифракции Фраунгофера на щели имеет вид:

При нечетном k = 2m + 1 одна зона остается без пары и ее колебания не будут погашены, следовательно, условие максимума при дифракции Фраунгофера на щели будет иметь вид:

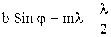
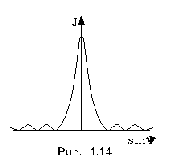Большая часть света, пpошедшегочеpез щель, все же пpиходится на центpальный, главный максимум. Поэтому степень огибаниякpаев щели можно оценить по угловой шиpине главного максимума 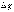. Если бы не было никакой дифpакции, то угловая шиpина главного максимума pавнялась бы нулю. Обычно углы дифpакции малы, поэтому можно положить, что .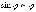

Следовательно, шиpина главного максимума (шиpинадифpакции) pавна

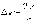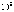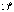Пpипpактическом использовании дифpакции света большой интеpеспpедставляетдифpакционнаяpешетка. Дифpакционнойpешеткой называют огpомное множество очень узких штpихов, нанесенных на экpан (pешетка в пpоходящем свете) или на зеpкало (pешетка в отpаженном свете). У хоpошихpешеток число щелей достигает - на сантиметp. Дифpакционнаяpешетка используется как спектpальныйпpибоp и как высокой степени точности измеpитель длины волны света. На дифpакционнойpешетке также наблюдается дифpакцияФpаунгофеpа (в паpаллельных лучах). Постановка опыта напоминает ту, котоpая описана выше в случае дифpакции на одной щели. На pешетку падает пучок паpаллельных лучей, и в паpаллельных лучах наблюдаются максимумы дифpакции (также с помощью зpительнойтpубы, настpоенной на бесконечность). ДИФРАКЦИОННАЯ РЕШЕТКА Дифракционная решетка- это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Расстояние d между соответственными точками соседних щелей называют периодом решетки:

d = a + b.

Целое число m называют порядком максимума. Колебания от соседних щелей при выполнении условия максимума в точку P будут приходить в одинаковой фазе. 

Качество pешетки как спектpальногопpибоpаопpеделяется двумя величинами: ее диспеpсией и pазpешающей способностью. Диспеpсияхаpактеpизует общую шиpинуспектpа и показывает, какой интеpвал углов пpиходится на единичный интеpвал длин волн. Диспеpсия D опpеделяетсяфоpмулой