Shpiry
.pdf
Смешанное произведение ве кторов — скал ярное произведение вектора a на векторно е произведение векторо в b и c .
Смешанное произведение ве кторов р авно определителю матрицы, составл енной из этих векторов.
Геометри чес кий смысл смешанного произведения.
Модуль смешанного произведения трех векторов a , b и с равен объёму пар аллелепип еда, образованного этими вектор ами :
Vпарал = | a · [ b × c ]|
Геометри чес кий смысл смешанного произведения.
Объем пир амиды обр азованной тр емя векторами a, b и с равен одной ш естой час ти о т модул я смешанного произведения этих векторо в:
1
|a · [ b × c ]|
6
Если смеш анного произведения трех н е нул евых векторов равно нулю, то эти вектора ко мпланарные. a · [ b × c ] = b · ( a · c ) - c · ( a · b )
a · [ b × c ] = b · [ c × a] = c · [ a × b ] = - a · [ c × b ] = - b · [ a × c ] = - c · [ b × a] a · [ b × c ] + b · [ c × a] + c · [ a × b ] = 0
----------------------------------------------------------------------------------------------------------------------------- -----
Уравнение плоскости в отрезках
где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.
Нормальное уравнение плоскости
где - |
углы, образуемые нормальным вектором |
плоскости с осями координат; p - расстояние от начала координат до плоскости.
Приведение общего уравнения плоскости к нормальному виду:
Здесь - нормирующий множитель плоскости, з нак
которого выбирается противоположным знаку D, если произвольно, если D = 0.
Уравнение плоскости по точке и нормальному вектору
В векторном виде
В координатах
------------------------------------------------------------------------------
Уравнение плоскости по точке и двум неколлинеарным векторам
Ввекторном виде
Вкоординатах
Уравнение плоскости по трем точкам
В векторном виде
В координатах
или
Параметрические уравнения плоскости
В векторном виде
В координатах
Уравнение плоскости, проходящей через две параллельные прямые и
Если прямые заданы соответственно уравнениями:
то уравнение плоскости есть
Уравнение плоскости, проходящей через две
пересекающиеся прямые и
или
Если, то уравнение
плоскости есть
Отклонение точки от плоскости
или
где знак перед корнем противоположен знаку D, если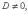 
и выбран произвольно, если D = 0.
Расстояние от точки до плоскости
Взаимное расположение двух плоскостей
Если, то они:
1)пересекаются
2)параллельны (но не совпадают)
3)совпадают
Если плоскости заданы |
|
уравнениями и |
то случаи 1 |
-3 имеют место, когда:
1)
2)
3)
Угол между плоскостями
Необходимое и достаточное условие перпендикулярности двух плоскостей
или
Расстояние между параллельными плоскостями
Если плоскости заданы уравнениями , то
а если уравнениями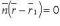 
и 
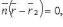то
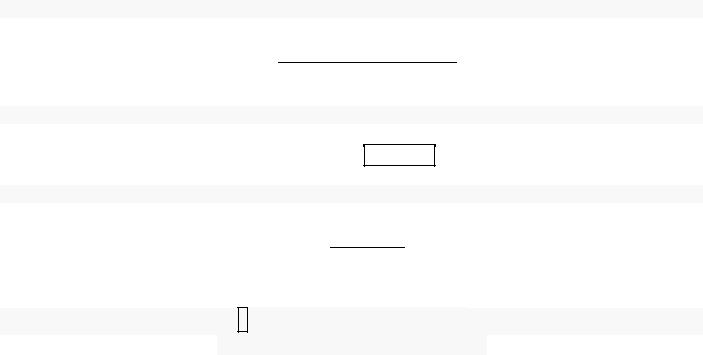
Расстояние от точки до плоскости.
d = |A·Mx + B·My + C·Mz + D|
√A2 + B2 + C2
Расстояние между плоскостями.
d = |D2 - D1| : √A2 + B2 + C2
Формула для вычисления расстояния от точки до прямой в пространстве
d = |M0M1×s| |s|
s - направляющий вектор прямой l
M1(x1, y1, z1) - точка лежащей на прямой