fizika_test

Вариант 1

1. Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

W= df/dt

Угловое ускорение - векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

 Угловое ускорение равно первой производной от угловой скорости по времени.

2. В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.

3. Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Уравнение моментов: момент инерции твердого тела, умноженный на вторую производную от угла (угловое ускорени) равен сумме моментов сил, действующих на тело.

4. Теоре́ма Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

J=Jc+md*d

Где Jc — известный момент инерции относительно оси, проходящей через центр масс тела,

J — искомый момент инерции относительно параллельной оси,

m — масса тела,

d — расстояние между указанными осями.

5. , где

__________________________________________

Вариант 2

1. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы. A=FS

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношениюработы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

2. В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.. Апериодичность

Если , то имеется два действительных корня, и решение дифференциального уравнения принимает вид: .В этом случае колебания с самого начала экспоненциально затухают.

Граница апериодичности

Если , два действительных корня совпадают , и решением уравнения является:

В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.. Слабое затухание

Если , то решением характеристического уравнения являются два комплексно сопряжённых корня­­­­­­­­­­­­­

3.декремент затухания (от лат. decrementum - уменьшение, убыль) (логарифмический декремент затухания) - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону.

4. Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси. 

5.

Вариант 3

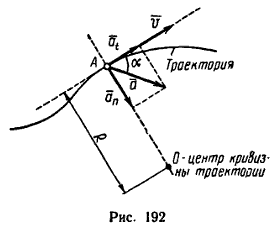
1.Быстрота изменения модуля скорости характеризуется касательным (тангенсальным) ускорением a_t – составляющей полного ускорения a, направленной по касательной к траектории (см. рис. 192).

Числовое значение касательного ускорения в общем случае определяется по формуле  a_t = dv/dt или a_t = f''(t).

Быстрота изменения направления скорости характеризуется центростремительным (нормальным) ускорением a_n – составляющей полного ускорения a, направленного по нормали к траектории в сторону центра кривизны.

Числовое значение нормального ускорения определяется в общем случае по формуле  a_n = v²/R,  где v – модуль скорости точки в данный момент;  R – радиус кривизны траектории в месте, где находится точка в данный момент.

2. В замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях тел этой системы между собой.

3. Потенциальная энергия  — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил.

4.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

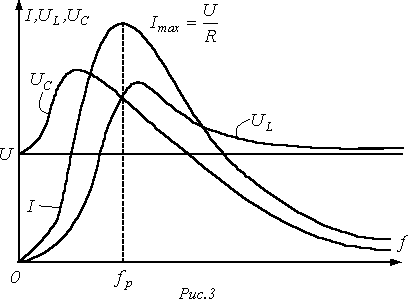
5. Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.

___________________________________________

Вариант 4.

1а. Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции.

1б.

2. сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твердыми смазочными материалами) — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя;жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды;

3. геометрическая точка, характеризующая движение тела или системы частиц как целого

Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

Где  — радиус-вектор центра масс,

 — радиус-вектор i-й точки системы,

 — масса i-й точки.

4.

.5. Решение одномерного волнового уравнения

 (функция  соответствует вынуждающей внешней силе)

с начальными условиями

имеет вид