
FIZIKA_MU_k_LB_Volnovaya_optika (1)
.pdf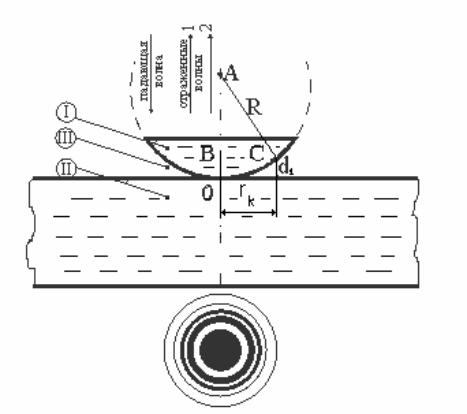
13 ОПРЕДЕЛЕНИЕ КРИВИЗНЫ ПОВЕРХНОСТИ ЛИНЗЫ
СПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
13.1Цель работы: применить на практике знания законов интерференции света, определить кривизну поверхности линзы с помощью колец Ньютона
13.2Указания по организации самостоятельной работы студентов
При подготовке к выполнению лабораторной работы самостоятельно проработать теорию [Савельев И.В. Курс общей физики.- М.: Наука, 1979. - Т.3 ,с.98-99; Ландсберг Г.С. Оптика. - М.: Наука, 1976,c.363-366].
В работе используется методика определения радиуса R кривизны сферической поверхности плосковыпуклой линзы 1 (рис.1) на основании интерференционной картины в виде концентрических светлых и темных колец, которую можно наблюдать при наложении двух когерентных волн 1 и 2, как отраженных от двух поверхностей воздушного зазора III между выпуклой поверхностью линзы I и плоской поверхностью отполированной стеклянной пластины II.
Рисунок 1
1
В выбранном наиболее простом варианте опыта монохроматический свет падает нормально поверхности пластины. Отраженные волны 1 и 2 являются когерентными, так как порождены одной падающей волной и из-за малой кривизны сферической поверхности линзы считаются распространяющимися вдоль нормали к пластине. Особенности кольцевой интерференционной картины обусловлены следующими факторами.
1.В точке О на рис.1.предполагается абсолютно полное прилегание линзы
кпластине, а, следовательно, отсутствие границы раздела сред и отраженных световых волн (темное пятно в центре).
2.Воздушный зазор имеет форму кольца, а его сечение – вид клина переменной толщины d.
3. Разность хода волн 1 и 2 формируется не только за счет двухкратного прохождения одной из волн воздушного зазора, но и за счет разных условий отражения световых волн от границы раздела сред I – III (линза-воздух) и III - II (воздух-пластина), что обусловлено потерей полуволны λ/2 при отражении этой волны от границы раздела со средой II большей оптической плотности.
= 2d −λ/ 2 |
(1) |
Для вывода рабочей формулы будем рассматривать только светлые кольца, что соответствует условиям интерференционных максимумов, для которых разность хода равна четному числу полуволн
= 2kλ/2, |
|
|
(2) |
|||
где k = 0,1,2,3,.............. |
|
|
|
|
|
|
Из сравнения формул (1) и (2) получим: |
|
|||||
2dk |
=(2k +1)λ/ 2 |
(3) |
||||
Для прямоугольного треугольника |
|
АВС можно записать: |
||||
R2 =(R −d |
k |
)2 +r2 |
|
|||
|
|
|
|
k |
|
|
Ввиду малости dk можно пренебречь величиной dk2 |
и получить: |
|||||
r2 |
= 2d |
k |
R |
|
|
|
k |
|
|
|
|
|
|
или
rk2 = R(2k +1)λ/ 2
Для вывода рабочей формулы удобно сравнивать кольца с номерами «k» «m» взяв разность:
r2 −r2 = R(k −m)λ |
|
|
k |
m |
|
Отсюда получаем формулу для расчета радиуса кривизны сферической |
||
поверхности линзы: |
(rk +rm )(rk −rm ) |
|
R = |
(4) |
|
|
(k −m)λ |
|
Рекомендация: Для большей точности следует руководствоваться условиями: 1) m > 3; 2) k/m > 1,5
2

13.3 Описание лабораторной установки
Лабораторная установка, схема которой и ход лучей приведены на рис. 2, состоит из микроскопа, осветителя со светофильтром, тест-объекта (линза и плоскопараллельная пластина в металлической оправке) и линейки для определения цены деления шкалы микроскопа
Рисунок 2
13.4 Порядок выполнения работы и методические указания по ее выполнению
Все операции настройки оптической системы выполняются с преподавателем.
1. Включить осветительную систему микроскопа. Длины волн монохроматического излучателя для различных светофильтров составляют:
-зеленый светофильтр λ = 0, 545 10-6 м.;
-желтый светофильтр λ = 0, 580 10-6 м.
2.Поворотом ручки револьверной системы выбрать объектив, который дает наибольшее увеличение.
3.Определить цену наименьшего деления измерительной шкалы микроскопа. Для этого надо положить линейку с делениями 1 мм на предметный столик микроскопа и поворотом ручек точной настройки навести на резкость. Определить количество делений шкалы микроскопа, которые укладываются в 1 мм линейки, вычислить цену деления.
4.Установить тест-объект. Добиться четкого изображения колец путем перемещения тубуса микроскопа М по вертикали ручками точной настройки.
3
Перемещая руками, объект на столике микроскопа добиться совмещения перекрестия координатных осей с центром системы колец Ньютона. По делениям на измерительной шкале микроскопа определить размеры 10-12 колец Ньютона. Произвести расчеты по формуле (4). Результаты измерений и расчетов занести в таблицу.
Таблица 4.1 Экспериментальные результаты
Номер |
Диаметр кольца, |
Радиус |
Радиус линзы |
< R >, |
кольца, |
дел |
кольца |
R, м |
м |
k,m |
|
rk ,m ,м |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
. |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
Оценить погрешность эксперимента.
13.5 Содержание отчета
Отчет должен содержать: цель работы; схему лабораторной установки, результаты измерений 10-12 радиусов колец ( rk ,m ); расчеты 10 радиусов
кривизны линзы (R ), среднее значение < R >, оценку их погрешности и вывод.
13.6 Контрольные вопросы и задания
1.Почему наблюдаемая интерференционная картина состоит из темных и светлых колец?
2.Вывести формулу RR . Радиусы каких колец нужно измерить, чтобы
погрешности были минимальными?
3.В чем состоит условие максимумов и минимумов света при интерференции когерентных лучей?
4.Что будет наблюдаться в центре, если опыт Ньютона проводить в проходящем свете?
5.Где плотнее расположены интерференционные кольца – в центре или на периферии? Почему?
6.Какова картина интерференции на воздушном зазоре (клине) между двумя плоскими стеклянными пластинами?
7.Почему радиус кривизны R линзы L должен быть большим?
4
14ИССЛЕДОВАНИЕ ДИФРАКЦИИ СВЕТА ОТ ЩЕЛИ
ВОПЫТЕ ФРАУНГОФЕРА
14.1 Цель работы: исследовать дифракцию на протяженной щели, в опыте Фраунгофера, установить соотношения между интенсивностями дифракционных максимумов освещенности, вычислить ширину щели.
14.2 Указания по организации самостоятельной работы студентов
Для изучения явления дифракции света следует проработать рекомендованную литературу [И.В.Савельев “Курс общей физики” т.2, 1982 г.
стр.400-407].
Дифракцией волн называется явление огибания волнами препятствий, отклонение волн от прямолинейного распространения и захода в область геометрической тени.
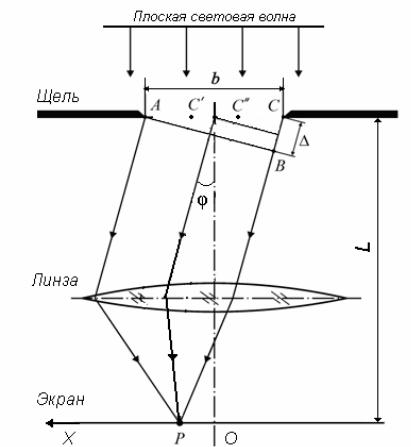
При дифракции Фраунгофера на щели дифрагированные лучи после щели идут параллельно. Поэтому результат такой дифракции плоской световой волны следует получать путем пропускания параллельных лучей через линзу и фокусирования их на конечном экране, расположенном в фокальной плоскости линзы (рис.1).
Рисунок 1 Начиная с линии АВ все лучи до точки Р на экране будут проходить
одинаковые оптические пути, т.е. будут таутохронными. Френель предложил
5
метод, по которому в соответствии с принципом Гюйгенса точечные источники вторичных сферических волн на линии щели АС можно разбить на группы, занимающие пространственные зоны: АС′, С′С′′ и т.д.
Зоны отличаются тем, что световые волны, посылаемые источниками, принадлежащими одной зоне, приходят в точку Р с отличием по фазе от средины этой зоны в пределах π/2. Следовательно разность хода лучей от
соседних зон до точки Р в среднем составляетλ2 . Зона АС′ отличается от
соседних зон длиной оптического пути. Максимальная разность этих путей для щели шириной b равна ∆:
=bsinϕ =CB
От двух соседних зон волны в точку Р приходят в противофазе, т.е. взаимно гасят друг друга. Следовательно, если на размере щели по отношению к точке Р укладывается четное число зон, то в точке Р наблюдается минимум освещенности, что соответствует условию:
∆ = 2k |
λ |
, |
(1) |
|
2 |
|
|
где k =1,2,3... Отсюда следует условие минимума:
bsinφ=2 k |
λ |
, |
(2) |
|
2 |
|
|
Если на максимальной разности хода ВС укладывается нечетное число полуволн, то на экране получается максимум освещенности, что соответствует условию:
bsinφ=(2 k +1) λ , |
(3) |
2
где k =0,1,2,3,4…
Более точный расчет интенсивности света на экране в зависимости от угла φ при дифракции Фраунгофера на щели, выполнений на основе принципа Гюйгенса-Френеля приводит к формуле:
|
sin |
2 π вsinϕ |
|
||||
|
|
λ |
|
|
|||
I (ϕ) = I0 |
|
|
|
|
|
||
|
π в |
|
2 |
|
|
||
|
, |
(4) |
|||||
|
|
|
|
sinϕ |
|||
|
|
λ |
|||||
|
|
|
|
|
|
|
|
где I0 - интенсивность в середине дифракционной картины, при φ=0. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
Если |
I0 -интенсивность центрального максимума |
нулевого |
порядка, то |
|||||||||||||||
I |
= I |
|
|
2 |
|
2 - |
есть интенсивность |
максимума |
первого |
порядка, |
|
I |
|
= I |
|
2 2 |
- |
|||||
0 |
|
|
|
|
2 |
0 |
|
|
||||||||||||||
1 |
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5π |
|
|||
второго и т.д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
2 2 |
|
|||
|
|
|
|
В |
итоге |
можно получить |
соотношения |
I0 : I1 : I2 |
: I3 :…=1: |
|
|
|
|
|
|
: |
|
|
: |
|||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 2 |
|
|
|
|
|
|
|
|
|
|
3π |
|
5π |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
…=1:0,045:0,016:0,008:… |
|
|
|
|
|
|
|
(5) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
7π |
|
|
|
|
|
|
|
|
|
|
||||||||||||
6

14.3 Описание лабораторной установки
Лабораторная установка (рис.2) включает оптическую скамью, на которой установлен лазер (1), как источник плоской монохроматической световой волны, рейтер со щелью (2), ширина которой регулируется, и фотодиодный цифровой координатный измеритель интенсивности излучения (3) для измерения положения дифракционных максимумов и их интенсивности.
Наличие фокусирующей линзы необязательно. Длина волны излучения лазера λ
= 0,63 10 – 6 м.
Рисунок 2
14.4 Порядок выполнения работы и методические указания по ее выполнению
1.Расположить на одном конце оптической скамьи лазер и рейтер со щелью, а на другом – координатный измеритель интенсивности света.
2.Включить лазер и установить приборы скамьи вдоль луча. Зафиксировать ширину “ b ” щели 0,12 – 0,15 мм
3.Измерить расстояние “L”между щелью и экраном.
4.Измерить координаты Хk и уровни освещенности Ik пяти максимумов.
Вычислить угловое положение φk=arctg |
хk |
|
максимумов. Занести полученные |
|||||||||
|
||||||||||||
|
|
|
|
|
|
L |
|
|
|
|
||
результаты в таблицу |
|
|
|
|
||||||||
Таблица 14.1 |
Экспериментальные результаты |
Ik/ Imax |
|
|
||||||||
k |
Хk |
|
φk=arctg |
хk |
|
|
Ik |
b |
|
|||
|
|
|
|
|||||||||
|
|
|
L |
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5.По формуле (3) вычислить ширину “ b ” щели и определить погрешность
ееизмерения. (Учесть как следствие первого замечательного предела, что в
радианах при φ → 0, φ ≈ sin φ ≈ tg φ).
7
6.При помощи фотодиодного цифрового измерителя яркости света
измерить интенсивности света Ik в положениях максимумов и занести результаты в таблицу.
7.Построить график зависимости относительной интенсивности
максимумов Ik/ Imax от угла φk. Для сравнения результатов эксперимента с теорией нанести на этот график теоретические значения освещенностей, приведенные в соотношении (4).
14.5 Содержание отчета
Отчет должен содержать: цель работы; схему лабораторной установки, таблицу с результатами измерений; графики зависимостей Ik = f (φk ) ,
полученные экспериментально и теоретически; оценку погрешностей; выводы.
14.6 Контрольные вопросы и задания
1.Сформировать принцип Гюйгенса.
2.Записать формулу, определяющую смысл принципа ГюйгенсаФренеля.
3.Охарактеризовать дифракцию Фраунгофера на щели.
4.Охарактеризовать дифракцию Френеля на круглом отверстии.
5.Какие лучи называют таутохронными?
6.Какая волна называется плоской?
7.Какая волна называется сферической?
8.Каким условиям удовлетворяют размеры пространственных зон в методе зон Френеля?
9.Записать условие максимумов для дифракции на щели.
10.Записать условие минимумов для дифракции на щели.
11.Что такое оптическая разность хода двух лучей?
12.Что такое разность фаз двух волн?
13.В чем отличие дифракции Френеля и дифракции Фраунгофера?
8
15. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДИФРАКЦИОННОЙ РЕШЕТКИ ПО ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЕ В ОПЫТЕ ЮНГА
15.1Цель работы: Рассчитать по интерференционной картине света расстояние между двумя щелевыми источниками монохроматического излучения и ширину щели.
15.2Указания по организации самостоятельной работы студентов
Для изучения явления интерференции света, его получения и использования следует проработать рекомендуемую литературу [И.В.Савельев
«Курс общей физики»,том 2,1978,C. 336-365]
Интерференция наблюдается только при суперпозиции волн, распространяющихся от когерентных источников. Когерентными называются источники, от которых волны приходят в каждую точку пространства с постоянной разностью фаз. Впервые наблюдал интерференцию световых волн английский физик Юнг в 1802 г.
Установка опыта Юнга состояла из трех экранов – I, II, III (рис.1). В первом из них имеется очень малое отверстие S, на которое падают плоские волны от интенсивного источника света. Согласно принципу Гюйгенса это отверстие является новым источником полусферических волн. Эти волны падают на два малых отверстия S1 и S2 во втором экране, которые, в свою очередь, становятся источниками двух систем волн одинаковой длины и фазы. За экраном II эти когерентные системы перекрывают друг друга и интерферируют. В тех местах экрана, где разность оптического хода волн соответствует нечетному числу полуволн
= (2k +1) |
λ |
, |
(1) |
|
2 |
|
|
k = 0, 1, 2, 3 ….
световые волны «гасят» друг друга Там же где разность хода равна четному числу полуволн
= 2k |
λ |
, |
(2) |
|
2 |
|
|
волны приходят в данную точку экрана в фазе и световые колебания усиливаются. Поэтому на экране III наблюдается чередование светлых темных полос. Если в качестве монохроматического излучателя S взять гелий-неоновый лазер, то полосы будут иметь красный цвет.
9
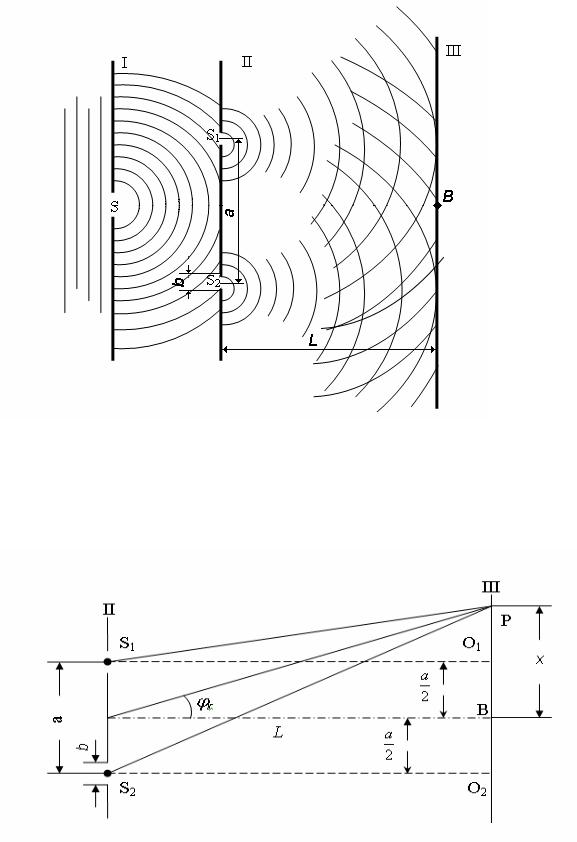
Рис.1
Если известно расстояние L между экранами II и III, расстояние между двумя соседними интерференционными полосами и длину интерферирующих волн, то можно определить расстояние между щелями d и ширину щели b.
Для вывода расчетной формулы воспользуемся рис.2.
Рис.2
Из рис.2 следует, что в точке В, отстоящей на равном расстоянии от S1 и S2, разность хода волн равна нулю. Здесь будет наблюдаться центральная светлая полоса – центральный самый яркий максимум освещенности.
Пусть в точке Р, произвольно выбранной на экране III, разность хода
10
