
Fizika_3_variant
.docx1 вопрос
Ускоре́ние (обычно обозначается , в теоретической механике ) — производная скорости по времени, векторная величина, показывающая, на сколько изменяется вектор скорости точки (тела) при её (его) движении за единицу времени (то есть ускорение учитывает не только изменение величины скорости, но и её направления).
Тангенциальное
ускорение — ![]() направлено
по касательной к траектории (обозначается
иногда
направлено
по касательной к траектории (обозначается
иногда ![]() и т. д.,
в зависимости от того, какой буквой в
данной книге принято обозначать
ускорение). Является составляющей
вектора ускорения a.
Характеризует изменение скорости по
модулю.
и т. д.,
в зависимости от того, какой буквой в
данной книге принято обозначать
ускорение). Является составляющей
вектора ускорения a.
Характеризует изменение скорости по
модулю.
![]()
Центростремительное
ускорение или Нормальное ускорение ![]() —
возникает (не равно нулю) всегда при
движении точки по окружности (конечного
радиуса) (также обозначается
иногда
—
возникает (не равно нулю) всегда при
движении точки по окружности (конечного
радиуса) (также обозначается
иногда ![]() и т. д.).
Является составляющей вектора
ускорения a,
перпендикулярной вектору мгновенной
скорости. Вектор нормального ускорения
всегда направлен к центру окружности,
а модуль равен:
и т. д.).
Является составляющей вектора
ускорения a,
перпендикулярной вектору мгновенной
скорости. Вектор нормального ускорения
всегда направлен к центру окружности,
а модуль равен:
![]() Полное
ускорение при
криволинейном движении складывается
из тангенциального и нормального
ускорений по правилу сложения
векторов и определяется формулой:
Полное
ускорение при
криволинейном движении складывается
из тангенциального и нормального
ускорений по правилу сложения
векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
-
=
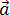 τ
+
τ
+
 n
n
____________________________
ВОПРОС 3
Потенциальная энергия — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином. (связь) Потенциальная энергия тела U(x,y,z), находящегося в точке с координатами (x,y,z) равна работе, которую совершают силы взаимодействия при перемещении тела из данной точки, в точку с координатами (x0,y0,z0), где потенциальная энергия принимается равной нулю U(x0,y0,z0) = 0.
_____________________________
ВОПРОС 5
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы.
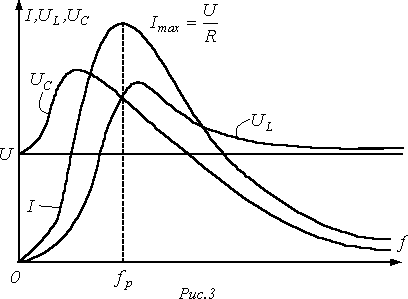
Резонансными
кривыми называются
зависимости тока и напряжения от
частоты. В качестве их примера на рис.
3 приведены типовые кривые I(f); ![]() при U=const. и для цепи на рис. 1
при U=const. и для цепи на рис. 1
___________________________
ВОПРОС 4
Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача - найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания
Сложим гармонические колебания одного направления и одинаковой частоты
![]()
воспользовавшись
методом вращающегося вектора
амплитуды.. Taк как
векторы A1 и
А2 вращаются
с одинаковой угловой скоростью 0,
то разность фаз (2—1) между
ними остается постоянной. Очевидно,
что уравнение результирующего колебания
будет![]() (144.1)
(144.1)
В
выражении (144.1) амплитуда А и
начальная фаза соответственно
задаются соотношениями![]() Проанализируем
выражение (144.2) в зависимости от разности
фаз (2—1):
Проанализируем
выражение (144.2) в зависимости от разности
фаз (2—1):
1) 2—1 = ±2m (т=0, 1, 2, ...), тогда A=A1+A2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
2) 2—1 = ±(2m+1) (т=0, 1, 2, ...), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны и +, причем <<. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
![]()
![]() (144.3)
(144.3)
Результирующее
колебание (144.3) можно рассматривать как
гармоническое с частотой ,
амплитуда Аб, которого
изменяется по следующему периодическому
закону:![]() (144.4)
(144.4)
Частота изменения Аб в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний:
![]()
_________________________
ВОПРОС 2
Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
