
Уравнение Шредингера для атома водорода, его решение (результаты). Квантовые числа. Квантование энергии, момента импульса и проекции момента импульса.
КВАНТОВЫЕ ЧИСЛА
Главное квантовое число
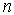 .
Это квантовое число принимает значения
.
Это квантовое число принимает значения
![]()
и определяет полную энергию электрона в любом квантовом состоянии
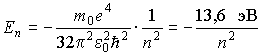 2.
Орбитальное
квантовое число
2.
Орбитальное
квантовое число
![]() .
В квантовых состояниях с заданным
значением главного квантового числа
.
В квантовых состояниях с заданным
значением главного квантового числа
![]() орбитальное квантовое число может
орбитальное квантовое число может
![]() .
.
![]() в
любом квантовом состоянии атом водорода
обладает не только механическим моментом
в
любом квантовом состоянии атом водорода
обладает не только механическим моментом![]() ,
величина которого определяется формулой(5.38),
но и магнитным моментом.
,
величина которого определяется формулой(5.38),
но и магнитным моментом.
![]()
Здесь универсальная постоянная
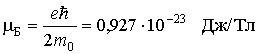
3.
Магнитное
квантовое число
![]() .
В квантовом состоянии с заданным
значением орбитального квантового
числа
.
В квантовом состоянии с заданным
значением орбитального квантового
числа
![]() ,
магнитное квантовое число может принимать
,
магнитное квантовое число может принимать![]() различных
значений из ряда
различных
значений из ряда
![]() .
.
![]() .
.
![]() Спин
— это собственный момент импульса
электрона, не связанный с движением в
пространстве. Для всех электронов
абсолютное значение спина всегда
равно s =
1/2. Проекция спина на ось = (магнитное
спиновое число ms)
может иметь лишь два значения: ms =
1/2 или ms =
-1/2
.
Электронный
слой атома образуют
электроны с одинаковой энергией, т. е.
с одинаковым n во всех состояниях.
В
зависимости от главного квантового
числа n
различают такие слои:
n=1
– K-слой
n=2
– L-слой
n=
3- M-
слой
n=4
– N-
слой
Спин
— это собственный момент импульса
электрона, не связанный с движением в
пространстве. Для всех электронов
абсолютное значение спина всегда
равно s =
1/2. Проекция спина на ось = (магнитное
спиновое число ms)
может иметь лишь два значения: ms =
1/2 или ms =
-1/2
.
Электронный
слой атома образуют
электроны с одинаковой энергией, т. е.
с одинаковым n во всех состояниях.
В
зависимости от главного квантового
числа n
различают такие слои:
n=1
– K-слой
n=2
– L-слой
n=
3- M-
слой
n=4
– N-
слой
АТОМ ВОДОРОДА С ТОЧКИ ЗРЕНИЯ КВАНТОВОЙ МЕХАНИКИ Потенциальная энергия электрона в электрическом поле ядра определяется выражением
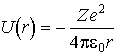 Движение электрона в таком поле можно
рассматривать как движение в некоторой
сферической потенциальной яме, форма
которой электрона на
Движение электрона в таком поле можно
рассматривать как движение в некоторой
сферической потенциальной яме, форма
которой электрона на
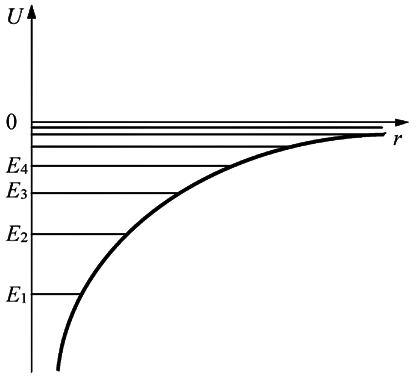
спектр
энергии электрона в атоме будет
дискретным, то есть состоять из отдельных
энергетических уровней со значениями
электр энергии электрона
![]() ,
,![]() ,
,![]() и
т.д.
и
т.д.
Состояние
электрона в атоме описывается волновой
функцией, что удовлетворяет уравнение
Шредингера:
![]() При переходе от прямоугольных координат
к сферическим уравнение разделяется
на 3 уравнения, каждое из которых зависит
от одной координаты. Решение будет иметь
место только тогда, когда каждое уравнение
будет равно целому числу. В результате
решения будем иметь 3 целых числа -
квантовых числа.
При переходе от прямоугольных координат
к сферическим уравнение разделяется
на 3 уравнения, каждое из которых зависит
от одной координаты. Решение будет иметь
место только тогда, когда каждое уравнение
будет равно целому числу. В результате
решения будем иметь 3 целых числа -
квантовых числа.
Механический и магнитный момент электрона. Гиромагнитное соотношение. Магнетон Бора.
Из
квантово-механической теории атома
водорода следует, что модуль момента
импульса электрона может принимать
следующие дискретные значения:
![]() где l – так
называемое орбитальное
квантовое число, l =
0, 1, 2, … n-1. Таким
образом, момент импульса электрона, как
и энергия, квантуется, т.е.
принимает дискретные
значения.
Заметим, что при больших значениях
квантового числа l (l >>1)
уравнение (40) примет вид
где l – так
называемое орбитальное
квантовое число, l =
0, 1, 2, … n-1. Таким
образом, момент импульса электрона, как
и энергия, квантуется, т.е.
принимает дискретные
значения.
Заметим, что при больших значениях
квантового числа l (l >>1)
уравнение (40) примет вид ![]() .
Это не что иное, как один из постулатов
Н. Бора.
Из
квантово-механической теории атома
водорода следует еще один важный
вывод: проекция
момента импульса электрона на какое-либо
заданное направление в пространстве z(например,
на направление силовых линий магнитного
или электрического поля) также квантуется по
правилу:
.
Это не что иное, как один из постулатов
Н. Бора.
Из
квантово-механической теории атома
водорода следует еще один важный
вывод: проекция
момента импульса электрона на какое-либо
заданное направление в пространстве z(например,
на направление силовых линий магнитного
или электрического поля) также квантуется по
правилу:
![]() где m =
0, ± 1, ± 2, …± l –
так называемое магнитное
квантовое число.
Электрон,
движущийся вокруг ядра, представляет
собой элементарный круговой электрический
ток. Такому току соответствует магнитный
момент pm .
Очевидно, что он пропорционален
механическому моменту импульса L.
Отношение магнитного момента pm электрона
к механическому моменту
импульса L называется гиромагнитным
отношением.
Для электрона в атоме водовода.
где m =
0, ± 1, ± 2, …± l –
так называемое магнитное
квантовое число.
Электрон,
движущийся вокруг ядра, представляет
собой элементарный круговой электрический
ток. Такому току соответствует магнитный
момент pm .
Очевидно, что он пропорционален
механическому моменту импульса L.
Отношение магнитного момента pm электрона
к механическому моменту
импульса L называется гиромагнитным
отношением.
Для электрона в атоме водовода.
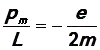 (знак
минус показывает, что вектора магнитного
и механического моментов направлены в
противоположные стороны). Отсюда можно
найти так называемый орбитальный
магнитный момент электрона:
(знак
минус показывает, что вектора магнитного
и механического моментов направлены в
противоположные стороны). Отсюда можно
найти так называемый орбитальный
магнитный момент электрона:
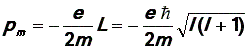 Эта
величина также квантуется.
Эта
величина также квантуется.
В
формуле (43) величина ![]() является
константой. Обозначим её mв и
назовем магнетоном
Бора.
Магнетон Бора служит естественной
единицей магнитного момента электрона,
так как значения магнитного момента
кратны величине mв :
является
константой. Обозначим её mв и
назовем магнетоном
Бора.
Магнетон Бора служит естественной
единицей магнитного момента электрона,
так как значения магнитного момента
кратны величине mв :
![]()
Плотность вероятности для электрона в атоме водорода.
Состояние
частицы в квантовой механике описывается
заданием волновой функции ![]() ,
являющейся функцией пространственных
координат и времени.
Волновая
фунция имеет статистический характер
и связана с Волнами де Бройля, т.е. квадрат
модуля амлитуды волн де Бройля в данной
точке пространства яляется мерой
вероятности обнаружения частицы в
данной точке пространства.
,
являющейся функцией пространственных
координат и времени.
Волновая
фунция имеет статистический характер
и связана с Волнами де Бройля, т.е. квадрат
модуля амлитуды волн де Бройля в данной
точке пространства яляется мерой
вероятности обнаружения частицы в
данной точке пространства.
Вероятностный смысл волновой функции в квантовой механике:
Квадрат
модуля волновой функции ![]() определяет
плотность вероятности
определяет
плотность вероятности![]() того,
что в момент времени
того,
что в момент времени![]() частица
может быть обнаружена в точке
пространства
частица
может быть обнаружена в точке
пространства![]() с
координатами
с
координатами![]() ,
,![]() и
и![]() .
.
Следовательно
![]() .
.
Плотность
вероятности |Ψ|2достигает
максимального значения на некотором
конечном расстоянии от ядра. При этом
наиболее вероятное значение r для
электрона атома водорода равно радиусу
орбиты a0 соответствующей
основному состоянию электрона в модели
Бора.

Рис. 1. Радиальное распределение вероятности пребывания электрона для основного энергетического состояния атома водорода
В простейшем случае уравнение Шредингера может быть записано в виде
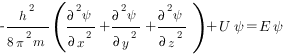
где h — постоянная Планка; m — масса частицы; U — потенциальная энергия; Е — полная энергия; х, у, z — координаты; Ψ — волновая функция.
Решая уравнение Шредингера, находят волновую функцию Ψ=f(x, y, z). Решение уравнения Шредингера возможно лишь при определенных значениях полной энергии Е. Определив вероятностную функцию можно оценить величину |Ψ|2dV — вероятность нахождения электрона в объеме пространства dV, окружающего атомное ядро.
Атом в магнитном поле. Опыт Штерна и Герлаха. Спин электрона.
Орбитальный
магнитный момент. В
квантовой теории магнитный момент μ
и механический момент М
атома
следует заменить операторами
![]() и
и
![]() :
:
|
|
(13.46) |
Отсюда
следует, что изучение свойств магнитного
момента электрона
сводится к изучению свойств операторов
![]() и
и![]() .
А так как операторы
.
А так как операторы
![]() и
и
![]() ,
,![]() и
и![]() отличаются
друг от друга только постоянным
множителем, то их свойства совершенно
аналогичны: магнитный и механический
моменты квантуются по одинаковым
правилам.
отличаются
друг от друга только постоянным
множителем, то их свойства совершенно
аналогичны: магнитный и механический
моменты квантуются по одинаковым
правилам.
В
стационарном состоянии определенные
значения могут иметь только модуль
магнитного
момента
![]() и одна из его проекций на произвольную
осьZ.
Имея
в виду (13.46), а также (13.34) и (13.36), запишем
собственные значения операторов
и одна из его проекций на произвольную
осьZ.
Имея
в виду (13.46), а также (13.34) и (13.36), запишем
собственные значения операторов
![]() и
и![]() :
:
|
|
(13.47) | |
|
μLz = -μБ mL, mL = 0, ± 1, ± 2, …, ± L, |
(13.48) | |
где μБ — магнетон Бора: μБ = eћ/2mc. Он играет роль кванта магнитного момента (точнее его проекции μz).
Спин — это собственный момент импульса электрона, не связанный с движением в пространстве. Для всех электронов абсолютное значение спина всегда равно s = 1/2. Проекция спина на ось = (магнитное спиновое число ms) может иметь лишь два значения: ms = 1/2 или ms = -1/2 . Электронный слой атома образуют электроны с одинаковой энергией, т. е. с одинаковым n во всех состояниях. , спиновый магнитный момент и его проекция на произвольную ось Z определяются как
|
|
(13.50) |
|
μSz = -2μБ ms, ms=S,S-1, …, -S. |
(13.51) |
При S = 1/2 ms = +1/2 и -1/2.
Опыты Штерна и Герлаха. Наличие у атомов магнитных моментов и их квантование было доказано экспериментально Штерном и Герлахом (1921). В их опытах пучок атомов пропускался сквозь сильно неоднородное поперечное магнитное поле (рис. 13.10, а). Необходимая степень неоднородности поля достигалась с помощью специальной формы полюсных наконечников N и S электромагнита (рис. 13.10, б). После прохождения магнитного поля пучок атомов попадал на фотопластинку Р и оставлял на ней след.
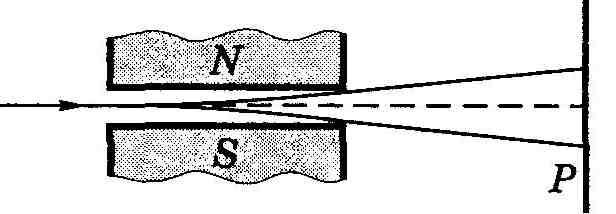
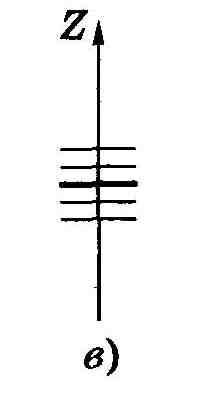
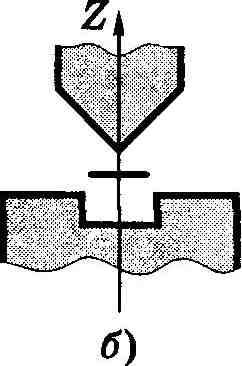
Рис. 13.10.
Если атомы обладают магнитным моментом, то согласно электродинамике на них будет действовать сила, проекция которой на ось Z (см. рис. 13.10, б)
|
|
(13.49) |
где μz — проекция магнитного момента атома на ось Z. Из этой формулы видно, что для получения необходимого эффекта при малых значениях μz нужно обеспечить достаточно большую неоднородность поля, т. е. ∂Bz/∂z. Это и достигалось с помощью указанной формы полюсных наконечников.
В отсутствие магнитного поля след пучка на фотопластинке Р имел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщепление пучка (рис. 13.10, в), что являлось следствием квантования проекции магнитного момента μz в формуле (13.49): μz может принимать только ряд дискретных значений. В опытах обнаружилось также, что для разных атомов число компонент, на которые расщеплялся пучок, было или нечетным, или четным. Анализ полученных результатов показал, что нечетное число компонент возникает у атомов, обладающих только орбитальным механическим моментом ML, тогда магнитное поле снимает вырождение по L и число компонент (значений mL) будет равно 2L + 1, т. е. нечетным.
Если же момент атома является суммой орбитального и спинового, т. е. определяется квантовым числом J, то число компонент будет равно 2J+ 1, и в зависимости от того, полуцелым или целым будет значение J, число компонент будет соответственно четным или нечетным.
Принцип Паули. Оболочка и под оболочка. Периодическая система элементов Менделеева.
принцип Паули: в любом квантовом состоянии может находиться не более одного электрона. Поэтому каждый следующий электрон невозбужденного атома должен занимать самый глубокий из еще незаполненных уровней. Тщательная проверка явилась подтверждением принципа Паули. Другими словами, в атоме (и в любой квантовой системе) не может быть электронов с одинаковыми значениями всех четырех квантовых чисел. Именно принцип Паули объяснил, почему электроны в атомах оказываются не все на самом нижнем дозволенном энергетическом уровне.
Данному значению п соответствует 2п2 состояний, отличающихся друг от друга значениями квантовых чисел ℓ, mℓ, ms. Совокупность электронов атома с одинаковыми значениями квантового числа п, образуют так называемую оболочку. В соответствии со значением п оболочки обозначают большими буквами латинского алфавита следующим образом:
-
Значение n
1
2
3
4
5
6
Символ оболочки
K
L
M
N
O
P
Оболочки подразделяют на подоболочки, отличающиеся квантовым числом ℓ. Различные состояния в подоболочке отличаются значениями квантовых чисел тℓ и ms. Число состояний в подоболочке равно 2(2l + 1). Подоболочки обозначают или большой латинской буквой с числовым индексом (К, L1, L2, …) или в виде
1S; 2s,2p; 3s,3p,3d; ...,
где цифра означает квантовое число п, т. е. принадлежность к соответствующей оболочке (К, L, М, ...). Возможные состояния электронов в атоме и их распределение по оболочкам и подоболочкам показано в табл. 13.2, в которой вместо обозначений ms = +1/2 и -1/2 использованы для наглядности стрелки ↑ и ↓. Видно, что число возможных состояний в К, L, М,... оболочках равно соответственно 2, 8, 18,..., т. е. равно 2п2. Полностью заполненные оболочки и подоболочки имеют L = 0 и S = 0, значит и J = 0. Это важный результат: при определенных квантовых числах L и S атома заполненные подоболочки можно не принимать во внимание.
Квантово-механическая формулировка принципа Паули определяется принципом тождественности одинаковых частиц: в системе одинаковых частиц реализуются только такие состояния, которые не меняются при перестановке местами двух частиц. В самом деле, если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Для фермионов, т.е. частиц с полуцелым спином, (а именно ими являются электроны) волновая функция является антисимметричной, поэтому два одинаковых фермиона, входящих в одну и ту же систему, не могут находиться в одинаковых состояниях.
Периодическая система химических элементов — это графическое выражение периодического закона. Периодический закон Менделеева устанавливает периодическое изменение свойств химических элементов в зависимости от увеличения зарядов ядер их атомов.
Пояснение строения периодической системы элементов:
1)порядковый номер химического элемента равен общему количеству электронов в атоме данного элемента; 2)уровни электронов в атоме определяется набором из 4 квартовых чисел. Разделение электронов в атоме по энергетических уровнях должен удовлетворять принципу минимума энергии: из увеличением числа электронов каждый следующий электрон должен занять возможный энергетический уровень с минимальной энергией;
3) заполнение электронами энергетических состояний в атоме должно происходить соответственно принципу Паули. Под электронной конфигурацией понимают состояние электронов с определенными значениями квантовых чисел n и l. Периодическое изменение свойств элементов с увеличением порядкового номера объясняется периодическим изменением числа электронов на их внешних энергетических уровнях. На каждом электронном слое может располагаться определенное число электронов: на первом — не больше двух, на втором — не больше восьми, на третьем — не больше восемнадцати. Число электронных слоев определяется по номеру периода, в котором расположен химический элемент. Число электронов на последнем (внешнем) слое определяется по номеру группы рассматриваемого элемента. Электронные слои заполняются у атомов постепенно, по мере увеличения общего числа электронов, которое соответствует порядковому номеру химического элемента. Количество электронов в каждой оболочке
Данное количество вычисляется по формуле:
![]()
-
s
p
d
f
g
Итого
K
2
2
L
2
6
8
M
2
6
10
18
N
2
6
10
14
32
O
2
6
10
14
18
50
