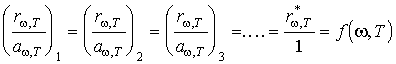1. Закони геометричної оптики

Закон прямолінійного поширення світла: у вакуумі й однорідному прозорому середовищі світло поширюється прямолінійно.

Закони відбивання світла

- падаючий і відбитий промені, а також перпендикуляр до межі двох середовищ, проведений із точки падіння променя, лежать в одній площині;

- кут падіння дорівнює куту відбивання.

Закони заломлення світла

- падаючий і заломлений промені, а також перпендикуляр до межі двох середовищ, проведений із точки падіння променя, лежать в одній площині;

- відношення синуса кута падіння до синуса кута заломлення для даних двох середовищ є сталою величиною, залежною від оптичних властивостей цих середовищ.

Закон незалежності світлових пучків: світлові пучки від різних джерел при накладанні діють незалежно один від іншого і не впливають один на одного.

2. Принцип Ферма.

Принцип Ферма - основний принцип геометричної оптики, який стверджує, що оптична довжина L \, реального променя, що проходить між точками P_1 \, та P_2 \, менша за оптичну довжину будь-якої іншої кривої, яку можна провести між цими двома точками.

L = \int_{P_1}^{P_2} n ds,

де n - показник заломлення, мінімальний для реального променя.

Інше формулювання полягає в тому, що промінь обирає таку траєкторію, щоб затратити найменший час на подолання віддалі між двома точками.

П'єр Ферма опублікував принцип найменшого часу в 1657, стверджуючи «природа завжди обирає найкоротший шлях».

Виходячи з принципу Ферма можна вивести усі закони геометричної оптики, наприклад, закон заломлення.

3. Інтерфере́нція (від лат. inter — взаємно, між собою; лат. ferio — вдаряю, вражаю) — явище накладання двох або більше когерентних світлових хвиль в результаті чого в одних місцях спостерігається підсилення результуючої хвилі (інтерференційний максимум), а в інших місцях послаблення (інтерференційний мінімум)

Не слід вважати, що інтерференцію світла можна спостерігати лише в лабораторних умовах, застосовуючи для цього спеціальні оптичні пристрої. Кожному не раз доводилося спостерігати райдужне забарвлення мильних плівок, тонких плівок нафти або мінерального масла, які плавають на поверхні води, кольори мінливості на поверхні загартованих стальних деталей, які покриті найтоншим прозорим шаром оксидів. Усі ці явища обумовлені інтерференцією світла в тонких прозорих плівках, яка виникає внаслідок накладання когерентних хвиль, що відбиваються від верхньої та нижньої поверхонь плівки.

Способы наблюдения интерференции (зеркала Френеля, бипризма Френеля.

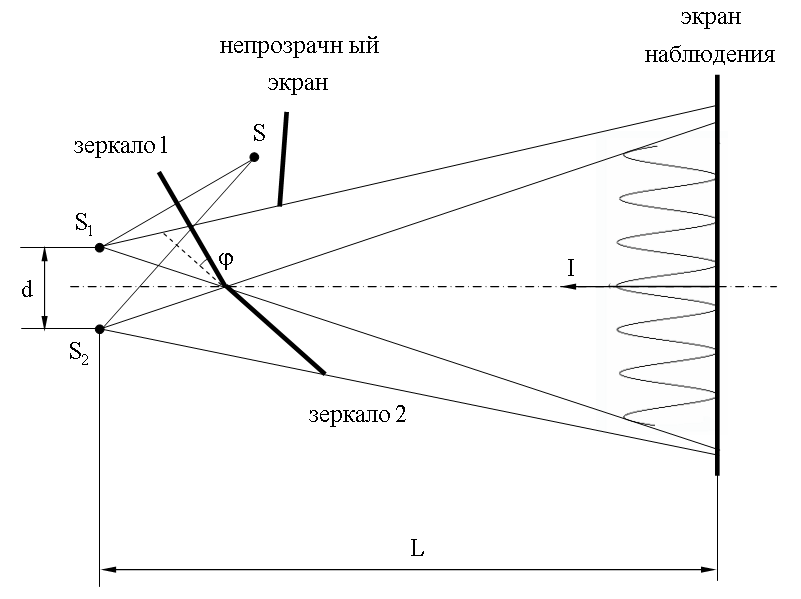
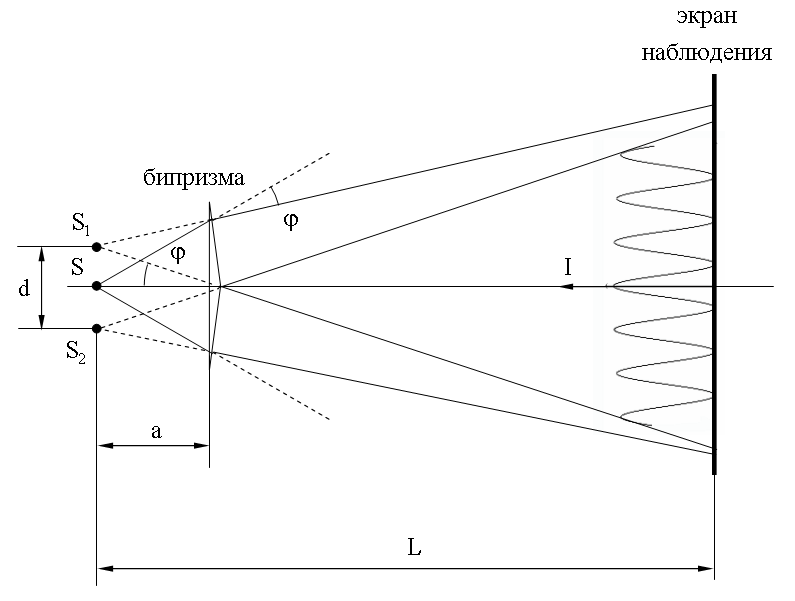Зеркала Френеля Свет от узкой щели S падает на два плоских зеркала, развернутых друг относительно друга на очень малый угол φ. Используя закон отражения света (17.1.3.) нетрудно показать, что падающий пучок света разобьется на два, исходящих из мнимых источников S₁ и S₂. Источник S закрывают от экрана наблюдения непрозрачным экраном. Бипризма Френеля Две стеклянные призмы с малым преломляющим углом θ изготавливают из одного куска стекла так, что призмы сложены своими основаниями, Источник света - ярко освещенная щель S. После преломления в бипризме падающий пучок расщепляется на два, исходящих от мнимых источников S₁ и S₂, которые дают две когерентные цилиндрические волны.

Так как преломляющий угол θ мал, то все лучи отклоняются каждой из половинок бипризмы на один и тот же угол φ . Можно показать, что в этом случае

,

здесь n - показатель преломления материала призмы.

Расстояние между источниками:

.

4. Явище інтерференції і дифракції світла підтверджують його хвильову природу. З хвильової точки зору пояснюють і явище поляризації, яке можна спостерігати тільки в поперечних хвилях. Світлову хвилю називають плоскополяризованою, якщо вектори напруженості електричного поля і магнітного поля в цій електромагнітній хвилі коливаються в певній площині. У природному світлі вектори і коливаються в довільних площинах, перпендикулярних до напряму поширення хвилі.

Рисунок 1

Поляризатором називається пристрій, який перетворює природне світло в поляризоване. Поляризатори мають властивість пропускати світлові хвилі з коливаннями вектора , який лежить тільки в одній площині (Рис.69).

5. Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка \frac{\rho^2}{z\lambda}, что сильно упрощает теоретическое рассмотрение явления. Здесь z — расстояние от отверстия или преграды до плоскости наблюдения, λ — длина волны излучения, а ρ — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля F \ll 1, при этом приходящие в точку волны являются практически плоскими

6. Дифракція світла

Дифракцією світла називається явище відхилення світла від прямолінійного напрямку поширення при проходженні поблизу перешкод. Як показує досвід, світло за певних умов може заходити в область геометричної тіні. Якщо на шляху рівнобіжного світлового пучка розташована кругла перешкода (круглий диск, кулька або круглий отвір у непрозорому екрані), то на екрані, розташованому на досить великій відстані від перешкоди, з'являється дифракційна картина – система почергових світлих і темних кілець. Якщо перешкода має лінійний характер (щілина, нитка, край екрана), то на екрані виникає система рівнобіжних дифракційних смуг.

Принцип Гюйгенса — Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых. Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

7. Одним з підтверджень наявності у фотонів маси та імпульсу є світловий тиск. У 1901 році П.М.Лебедєв вперше експериментально виявив і виміряв тиск світла на тверді тіла і гази. Прилад Лебедєва – це досить чутливі крутильні терези, рухома система яких складається з легкого каркаса із закріпленими на ньому тонкими кружками, які розміщені симетрично відносно осі підвісу. Деякі крильця були дзеркальними, а поверхня інших була затемнена. Згідно теорії світла Максвелла тиск чинить електромагнітна хвиля, що падає на поверхню:

р = , де Ее =

- енергетична освітленість поверхні, с- швидкість світла у вакуумі.

- коефіцієнт відбивання.

8. Дифракційна решітка — оптичний елемент з періодичною структурою, здатний впливати на поширення світлових хвиль так, що енергія хвилі, яка пройшла через ґратку, зосереджується в певних напрямках. Напрямки поширення цих пучків залежать від періоду ґратки та довжини світлових хвиль, тобто дифракційна ґратка працює як дисперсійний елемент. Монохроматичний світловий пучок, що падає на ґратку, теж розділиться на декілька пучків, які поширюються в різних напрямках. Дифракційні ґратки широко застосовуються у монохроматорах і спектрометрах.

Найпростіша дифракційна ґратка — тонка скляна пластинка, на поверхні якої нанесені прямолінійні паралельні рівновіддалені штрихи, ширина та відстань між якими сумірні з довжиною хвилі світла.

Принцип роботи дифракційної ґратки ґрунтується на дифракції світлових хвиль, які взаємодіють з нею, та подальшій інтерференції цих дифрагованих хвиль.

У загальному випадку дифракційну ґратку можна уявити собі, як сукупність багатьох паралельних та рівновіддалених прозорих щілин, розділених однаковими непрозорими проміжками. Якщо на таку ґратку буде падати світловий пучок, то світлові хвилі, проходячи крізь щілини ґратки, будуть дифрагувати. Кожна точка будь-якої щілини ґратки у такому разі виступатиме як точкове джерело світла. Таким чином, світлові хвилі після взаємодії з ґраткою будуть поширюватись у різних напрямках. Світлові хвилі від різних щілин ґратки, які поширюються в одному напрямку, інтерферують між собою. Якщо ці хвилі знаходяться у фазі, то вони підсилюють одна одну, якщо у протифазі, то гасять. У першому випадку відбувається конструктивна інтерференція, в другому — деструктивна. Напрямки поширення дифрагованих хвиль, на яких відбувається їх конструктивна інтерференція, називаються дифракційними максимумами. Таких максимумів зазвичай кілька, їх позначають цілими числами, які називаються порядком дифракції. Кількість дифракційних максимумів та напрямки їх поширення залежать від періоду гратки та довжини хвилі світла і можуть бути визначені за допомогою рівняння дифракційної ґратки:

d \left( \sin{\theta_m(\lambda)} + \sin{\theta_i} \right) = m \lambda , де

θi — кут падіння світлового пучка на ґратку,

θm(λ) — кут дифракції для пучка m-го порядку,

λ — довжина хвилі світла,

d — період гратки,

m — порядок дифракції.

Із цього рівняння випливає, що кут дифракції залежить від довжини хвилі світла. Отже, якщо на ґратку падатиме біле світло, то воно розкладатиметься ґраткою у спектр.

9. Дисперсія світла — залежність показника заломлення (або діелектричної проникності) середовища від частоти хвилі світла.

Здебільшого показник заломлення зростає при збільшенні частоти. Це зростання називають нормальною дисперсією. Аномальна дисперсія — зменшення показника заломлення при збільшенні частоти — виникає в спектральних областях, близьких до частот інтенсивного поглинання.

10. Явище інтерференції і дифракції світла підтверджують його хвильову природу. З хвильової точки зору пояснюють і явище поляризації, яке можна спостерігати тільки в поперечних хвилях. Світлову хвилю називають плоскополяризованою, якщо вектори напруженості електричного поля і магнітного поля в цій електромагнітній хвилі коливаються в певній площині. У природному світлі вектори і коливаються в довільних площинах, перпендикулярних до напряму поширення хвилі.

Рисунок 1

Поляризатором називається пристрій, який перетворює природне світло в поляризоване. Поляризатори мають властивість пропускати світлові хвилі з коливаннями вектора , який лежить тільки в одній площині (Рис.69).

Поляризатор являє собою речовину, що дозволяє виділити з неполяризованого світла частину, яка має бажану поляризацію при пропущенні його через себе(речовину) або при відображенні від поверхні. Вони використовуються в поляризаційних фільтрах.

Поляризаційний фільтр - пристрій для отримання повністю або частково поляризованого оптичного випромінювання з випромінювання з довільними поляризаційними характеристиками. У фотографії поляризаційні фільтри використовуються для досягнення різних художніх ефектів (усунення відблисків, затемнення неба).

Закон Малюса — физический закон, выражающий зависимость интенсивности линейно-поляризованного света после его прохождения через поляризатор от угла \varphi между плоскостями поляризации падающего света и поляризатора.

I=k_{a}I_{0}\cos^2\varphi\;

где I0 — интенсивность падающего на поляризатор света, I — интенсивность света, выходящего из поляризатора, ka — коэффициент прозрачности поляризатора.

Установлен Э. Л. Малюсом в 1810 году.

В релятивистской форме

I=\frac{I_{0}}4(\frac{\omega\prime}\omega)^2(\frac{\omega}\omega\prime+\frac{\omega\prime}\omega-2+4\cos^2\varphi)

где ω и \omega\prime — циклические частоты линейно поляризованных волн, падающей на поляризатор и вышедшей из него

Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.

Это явление оптики названо по имени шотландского физика Дэвида Брюстера, открывшего его в 1815 году.

Закон Брюстера: \operatorname{tg}\left( {{\theta }_{Br}} \right)={{n}_{21}}, где n21 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).

12. Закон зміщення Віна дає залежність довжини хвилі, на якій потік випромінювання енергії чорного тіла сягає свого максимуму, від температури чорного тіла.

\lambda_{\max}=\frac{0{,}002898}{T}

де T — температура в кельвінах, а λmax — довжина хвилі з максимальною інтенсивністю у метрах. Слід зазначити, що коефіцієнт у даній формулі має при цьому розмірність [ м К].

14. Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.

Закон Кирхгофа. Это означает, что тела, интенсивнее поглощающие излучение какой-либо частоты, будут это излучение интенсивнее и испускать.

     Отношение испускательной и поглощательной способностей одинаково для всех тел в природе, включая абсолютно черное тело, и при данной температуре является одной и той же универсальной функцией частоты (длины волны).

      

16. Закон Стефана — Больцмана

Основная статья: Закон Стефана — Больцмана

Общая энергия теплового излучения определяется законом Стефана — Больцмана, который гласит:

Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:

j=\sigma T^4\,\!,

где j — мощность на единицу площади излучающей поверхности, а

\sigma=\frac{2 \pi^5 k^4}{15 c^2 h^3}=\frac{\pi^2 k^4}{60\hbar^3 c^2} \simeq 5{,}670400(40)\cdot 10^{-8} Вт/(м²·К4) — постоянная Стефана — Больцмана.

Таким образом, абсолютно чёрное тело при T = 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.

Для нечёрных тел можно приближённо записать:

j=\epsilon\sigma T^4,\

где \epsilon — степень черноты (для всех веществ \epsilon<1, для абсолютно чёрного тела \epsilon=1).

Константу Стефана — Больцмана σ можно теоретически вычислить только из квантовых соображений, воспользовавшись формулой Планка. В то же время общий вид формулы может быть получен из классических соображений (что не снимает проблемы ультрафиолетовой катастрофы).

17. Рівняння Шредінгера — основне рівняння нерелятивістської квантової механіки, яке визначає закон еволюції квантової системи з часом.

H \left| \psi (t) \right\rangle = i \hbar {d\over d t} \left| \psi (t) \right\rangle.,

де \left| \psi (t) \right\rangle — хвильова функція, H — гамільтоніан. Уперше це рівняння було записане Ервіном Шредінгером у 1926 році.

18. Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие рассеивания его электронами. Обнаружен американским физиком Артуром Комптоном в 1923 году для рентгеновского излучения. В 1927 Комптон получил за это открытие Нобелевскую премию по физике.

Иллюстрация к эффекту Комптона

При рассеянии фотона на покоящемся электроне частоты фотона \ \nu и \ \nu' (до и после рассеяния соответственно) связаны соотношением:

\nu'=\nu\;{1\over {1 + {h\nu\over {m_ec^2}}(1-\cos\Theta)}},

где \ \Theta — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

\ \lambda'-\lambda=\lambda_k(1-\cos\Theta),

где \lambda_k={h\over {m_ec}} — комптоновская длина волны электрона.

Для электрона \lambda_k=2,4263 \cdot 10^{-12} м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.