23.Частица в одномерной бесконечно глубокой потенциальной яме. Квантовая энергия.

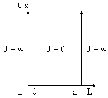
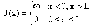
ПОТЕНЦИАЛЬНАЯ ЯМА Потенциальная энергия U удовлетворяет следующим граничным условиям При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е. (x) = 0       x < 0, x > LИспользуя станционарное уравнение Шредингера для случая U = 0, получим 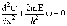Для бесконечной одномерной потенциальной ямы имеем следующее:

1. Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях. 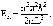где n = 1, 2, 3...

2. Частица может находиться в каком-то одном из множества энергетических состояний.

3. Частица не может иметь энергию равную нулю.

4. Каждому значению энергии E_n соответствует собственная волновая функция _n, описывающая данное состояние.

5. Для собственной функции ₁(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для состояния ₂(x) вероятность обнаружения частицы в этой точке равна 0 и так далее.

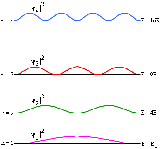Рис. 2. Плотности вероятности обнаружения частицы в различных квантовых состояниях.

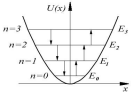
Уровни энергии по мере увеличения номера n сближаются.

24.Гармонический осциллятор в квантовой механике.

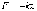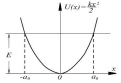
КВАНТОВЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР Одномерный гармонический осциллятор, совершающий колебания вдоль оси под действием возвращающей квазиупругой силы. Потенциальная энергия такого осциллятора имеет вид

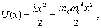       где 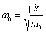- собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.   В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера с потенциальной энергией

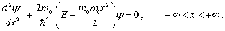
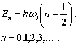 Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии 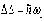друг от друга  Еще одной важной особенностью спектра является наличие так называемых нулевых колебаний - колебаний с энергией 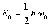, соответствующих значению квантового числа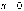. Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Отличие квантового осциллятора от классического

1.Энергия квантого осциллятора квантуется.

2.Уровни энергии эквидистантны и расстояние между ними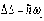 3. Существует энергия нулевых колебаний даже при абсолютном нуле.

4.При переходе квантовой системы в другое состояние существует правило отбора

∆=±n

5.В отличие от классического случая частицу можно найти за пределами потенциальной ямы

25.Прохождение частицы сквозь потенциальный барьер. Туннельный эффект.

ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙ БАРЬЕР Тунне́льный эффект — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Явление реальное и наблюдается при автоэлектронной эмиссии, когда происходит вырывание электронов из металла при напряженности поля меньшей напряженности необходимой для преодаления поверхностного скачка потенциала. Явление автоионизации связано с вырыванием электронов из отдельных атомов и молекул под действием электрического поля.  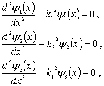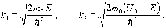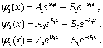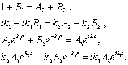Уравнение Шредингера в областях I, II и III имеет вид    где   Волновые функции, являющиеся решением уравнений   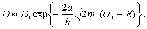     коэффициент прохождения частицы через порог . 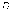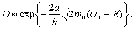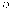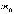коэффициент прохождения испытывает сильную (экспоненциальную) зависимость от ширины барьера , массы частицы и разности энергий .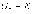

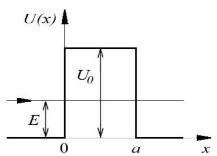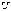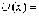
Область пространства, в которой потенциальная энергия частицы больше, чем в окружающих областях, называетсяпотенциальным барьером. Анализ движения частицы в области потенциального барьера начнем с рассмотрения простейшего случая одномерного прямоугольного потенциального барьера (рис.4.8) . Пусть потенциальная энергия частицы имеет вид После прохождения барьера волна принимает вид волны с меньшей амплитудой,а внутри будет вид експаненты, но энергия останется прежней. Туннельный эффект – явление сугубо квантовое. Говорить об отрицательной энергии кинетической энергии барьера не умеет смысла, т.к. из-за принципа неопределенности нельзя полную энергию представить в виде суммы кинетической и потенциальной энергий. Однако, полная энергия частицы - величина определенная и закон сохранения энергии выполняется.