Степень вершины

Число ребер, инцидентных некоторой вершине v, называетсястепеньювершины и обозначается degv. В полном графеК_пстепень каждой вершины равна п– 1. максимальная и минимальная степени вершин графаGобозначаются символами(G) и(G) соответственно:

.

Вершина степени 0 называется изолированной, вершина степени 1 –концевой(висячей). Ребро, инцидентное концевой вершине, также называетсяконцевым. Вершина графа, смежная с каждой другой его вершиной, называетсядоминирующей.

Пример 2. В графеН₃ на рис 2.11 вершина 3 – висячая, вершина 2 – доминирующая,.

Пути в графах

Чередующаяся последовательность

(2.1)

вершин и ребер графа, такая что (i = 1, 2, …,l), называетсяпутем, соединяющим вершины и(или (, )-путем). Очевидно, что путь можно задать последовательностью

его вершин, а также последовательностью его ребер

.

Г

Рис. 2.14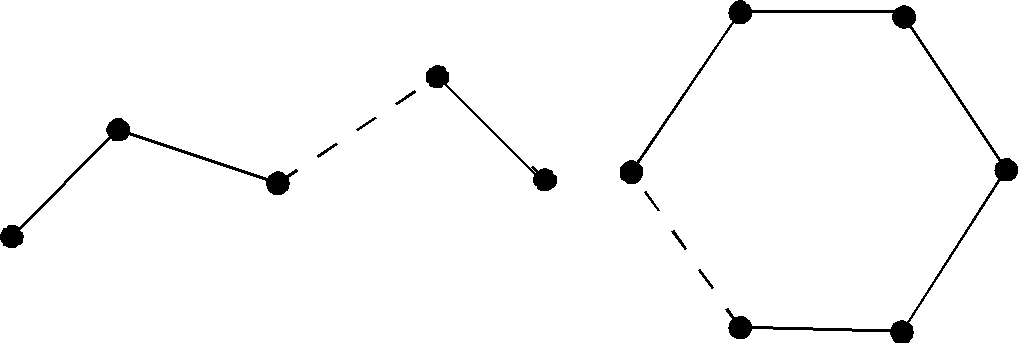

раф называетсясвязным, если любые две несовпадающие вершины в нем соединены маршрутом.

Путь называется простым, если все его вершины, кроме, может быть, крайних, различны. Путь называетсяцепью, если все его ребра различны, ипростой цепью, если все его вершины различны. Путь (2.1) называется циклическим, если. Циклическая цепь называетсяциклом, а циклическая простой путь –простым циклом. Простую цепь, имеющуюпвершин, будем обозначатьC_n, простой цикл –Z_n( рис.2.14).

Число lребер в пути (2.1) называется егодлиной.

Пример 3. В графеGна рис 2.11 (1, 4, 5, 2, 4) – цепь; (1, 4, 5, 2, 3) – простая цепь; (1, 4, 5, 2, 4, 1) – циклический путь, не являющийся циклом; (4, 3, 2, 4) – цикл.

Метрические характеристики графа

Пусть G– граф, аи иv– две его несовпадающие вершины. Длина кратчайшего (и,v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинамиииv и обозначается черезd(u,v). Положим ещеd(u,и) = 0. Очевидно, что введенное таким образом расстояние удовлетворяетаксиомам метрики:

1. d(u, v)  0,

2. d(u,v) = 0 тогда и только тогда, когдаu = v,

3. d(u, v) = d(v, u),

4. d(u,v) +d(v,w)d(u,w) (неравенство треугольника).

Для фиксированной вершины ивеличина

называется эксцентриситетом вершины и. Максимальный из всех эксцентриситетов вершин графа называетсядиаметром графаGи обозначается черезd(G). Тем самым,

.

В

2

ершинаvназываетсяпериферийной, если.

Простая цепь длины d(G), расстояние между концами которой равноd(G), называетсядиаметральной цепью.

П

Рис. 2.15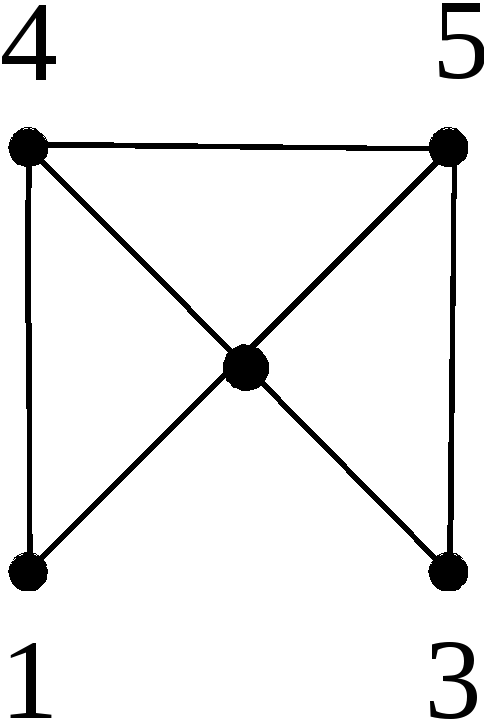

ример 4.В графе на рис. 2.15d(1,2) = 1,d(1, 3) = 2;е(1) = 2;d(G) = 2. Все вершины, кроме вершины 2 являются периферийными, (1, 2, 3) – диаметральная цепь.

Минимальный из эксцентриситетов вершин связного графа называется его радиусоми обозначаетсяr(G):.

Очевидно, что радиус графа не больше его диаметра.

Вершина называется центральной, если. Множество всех центральных вершин графа называется егоцентром. Граф может иметь единственную центральную вершину или несколько центральных вершин. Наконец, центр графа может совпадать с множеством всех вершин.

Решение типовых задач

1. Доказать, что сумма степеней всех вершин графа равно удвоенному числу ребер (лемма о рукопожатиях):.

Решение.Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 1 два раза (оно учитывается в степенях двух вершин). Поэтому сумма степеней всех вершин графа равно удвоенному числу ребер.

2. Найти все неизоморфные графы четвертого порядка.

Решение.У графа четвертого порядка число ребер может быть от 0 в пустом графеО₄ до 6 в полном графеK₄.

Если , получаем единственный графО₄.

Если – тоже единственный граф с двумя изолированными вершинами и двумя смежными друг другу.

При получаем два графа: ребра смежные и нет.

При имеем:. Если изолированных вершин нет, то возможные наборы степеней вершин: 1, 1, 2, 2 и 1, 1, 1, 3. Если изолированная вершина одна, то нет вершины со степенью 3, и возможный набор степеней вершин 2, 2, 2, т.е. цикл. Двух изолированных вершин быть не может.

Если , получаем, что из полного графа удалены два ребра: либо смежные, либо нет. Получаем два графа.

Если получаем единственный граф удалением из полного графа одного ребра.

В

Рис. 2.16

се неизоморфные графы порядка 4 представлены на рис. 2.16.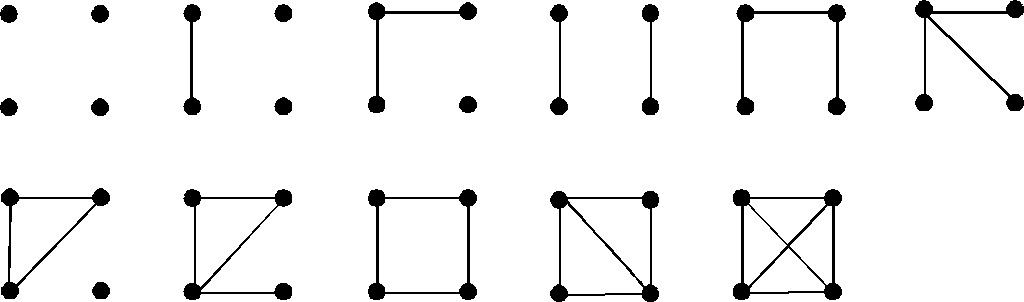

3. Доказать, что если число ребер графа порядка п> 2 больше, чем , то он связен.

Решение. Предположим, что он не связен. Тогда существуют две вершиныаиb, не связанные между собой. Обозначим черезV₁множество вершин, достижимых из, а черезV₂– множество вершин, достижимых изb. Тогда ни одна вершина изV₂не связана ни с какой вершиной из V₁. Пусть |V₁| =k<n,k> 0. Тогда | V₂| =n–k> 0. Еслиk= 1, то |V₂| =n– 1 и наибольшее значение |E| равно(когда подграф, порожденныйV₂– полный), что противоречит условию. Приk2 наибольшее значение достигается, если подграфы, порожденныеV₁ иV₂– полные. Тогда,, и для всего графа имеем

,

что противоречит условию, следовательно, исходный граф связен.

4. Доказать, что в связном графе любые две простые цепи максимальной длины имеют общую вершину.

Решение. Предположим, что у двух простых цепейимаксимальной длины нет общих вершин. Возьмем произвольно по одной вершине из каждой цепии. Так как граф связный, то существует путь изв. Выберем из отрезков цепей отдои отдотот, длина которого не меньше. Аналогично для. Составим новую простую цепь из этих отрезков и простой цепи, соединяющейи, ее длина больше, что противоречит тому, что исходные цепи максимальны.