
Изоморфизм графов
Легко
подсчитать число графов с фиксированным
множеством вершин V. Эти графы
различаются своими ребрами, и поэтому
их число равно количеству подмножеств
множестваVV,
т.е.![]() ,
гдеп= | V |. Однако эти графы на
всегда следует различать. Как в применении
теории графов, так и в самой этой теории
чаще существенно лишь то, что есть
объекты (вершины графа) и связи между
объектами (ребра графа). С этих позиций
графы, которые получаются один из другого
изменением наименований вершин, разумно
не различать. Такие графы называютсяизоморфными.
,
гдеп= | V |. Однако эти графы на
всегда следует различать. Как в применении
теории графов, так и в самой этой теории
чаще существенно лишь то, что есть
объекты (вершины графа) и связи между
объектами (ребра графа). С этих позиций
графы, которые получаются один из другого
изменением наименований вершин, разумно
не различать. Такие графы называютсяизоморфными.
Пусть
GиН– графы, а![]() –
биекция. Если для любых вершинииvграфаG их образы
–
биекция. Если для любых вершинииvграфаG их образы![]() и
и![]() смежны
вН тогда и только тогда, когдаииvсмежны вG, то эта биекция
называетсяизоморфизмом графа G на
граф Н. Если такой
изоморфизм существует, то мы пишем
смежны
вН тогда и только тогда, когдаииvсмежны вG, то эта биекция
называетсяизоморфизмом графа G на
граф Н. Если такой
изоморфизм существует, то мы пишем
![]() и
говорим, что графыGиН изоморфны.
и
говорим, что графыGиН изоморфны.
П
Рис. 2.8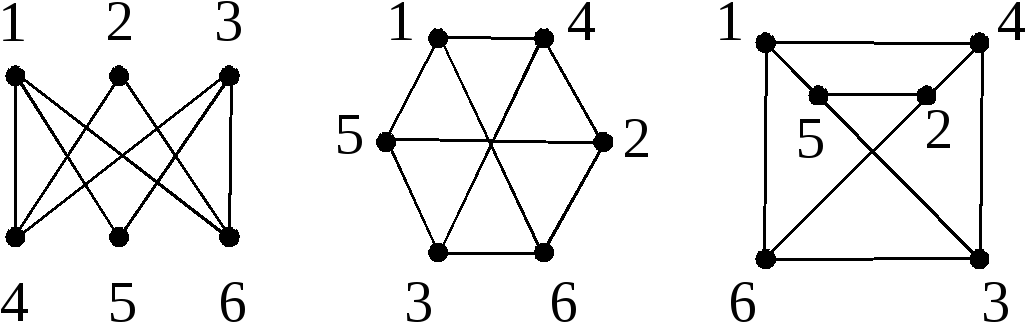
О
Рис. 2.9
В
Рис. 2.10.
Число gnпомеченных графов порядкапопределяется сложно. Известнаформула Пойа
![]() ,
,
дающая
асимптотику числа gn. Эта
формула означает, что две функцииg(п)=gn
иf(n)=
![]() асимптотически равны, т.е.
асимптотически равны, т.е.![]() .
.
Операции над графами
Граф Нназываетсяподграфом(иличастью) графаG, еслиVHVG,ЕHЕG. ПодграфНназываетсяостовным подграфом, еслиVH=VG. Если множество вершин подграфаНестьU, а множество его ребер совпадает с множеством всех ребер графаG, оба конца которых принадлежатU, тоНназываетсяподграфом, порожденным множеством U. На рис.2.11 изображены графGи три его подграфаН1,Н2иН3 , среди которыхН3 является остовным, аН2– порожденным.
Г
Рис. 2.11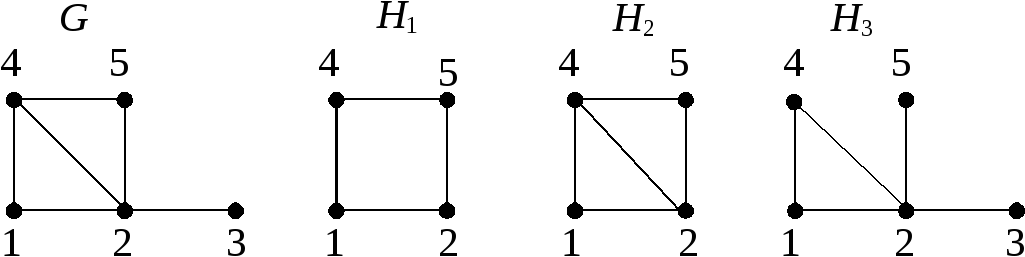
В
Рис.
2.12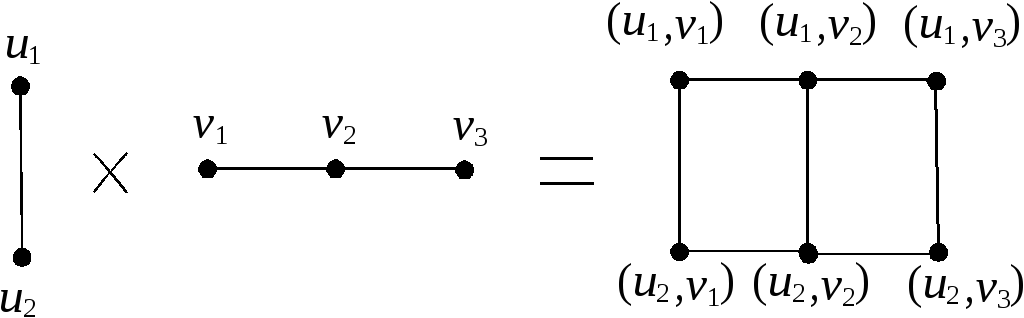
![]() называется граф, для которого
называется граф, для которого![]() – декартово произведение множеств
вершин исходных графов, аE(G)
определяется следующим образом: вершины
(и1,и2) и (v1,v2) в графеGсмежны тогда
и только тогда, когда илии1=v1, аи2 иv2 смежны вG2, илии2=v2, аи2 иv2
смежны вG1(рис. 2.12).
– декартово произведение множеств
вершин исходных графов, аE(G)
определяется следующим образом: вершины
(и1,и2) и (v1,v2) в графеGсмежны тогда
и только тогда, когда илии1=v1, аи2 иv2 смежны вG2, илии2=v2, аи2 иv2
смежны вG1(рис. 2.12).
Очевидно,
что
![]() ,
,
![]() .
.
С
помощью операции произведения можно
определить п-мерный куб![]() рекуррентно:
рекуррентно:![]() .
.
Покажем,
что это определение совпадает с данным
ранее. Действительно,
![]() .
Вершины графа
.
Вершины графа![]() можно представить векторами длиныпиз 0 и 1 таким образом, что две вершины
будут смежны тогда и только тогда, когда
соответствующие векторы различаются
в одной координате.
можно представить векторами длиныпиз 0 и 1 таким образом, что две вершины
будут смежны тогда и только тогда, когда
соответствующие векторы различаются
в одной координате.
Д
Рис. 2.13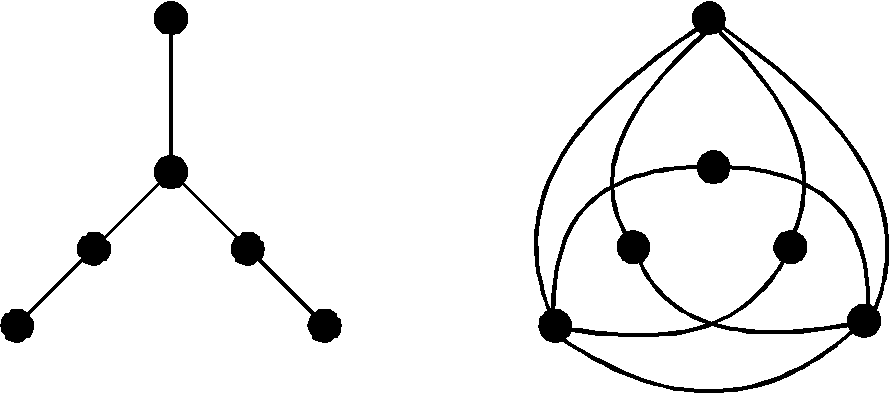
![]() :
:![]() ,
и две несовпадающие вершины смежны в
,
и две несовпадающие вершины смежны в![]() тогда и только тогда, когда они не смежны
вG:
тогда и только тогда, когда они не смежны
вG: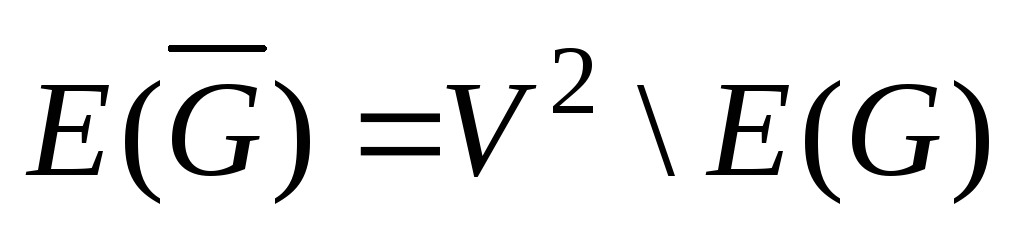 (рис.
2.13).
(рис.
2.13).
Граф, изоморфный своему дополнению, называется самодопол-нительным.
