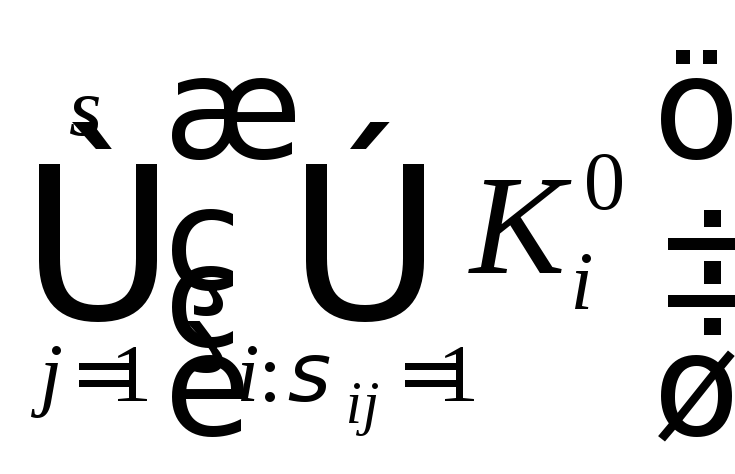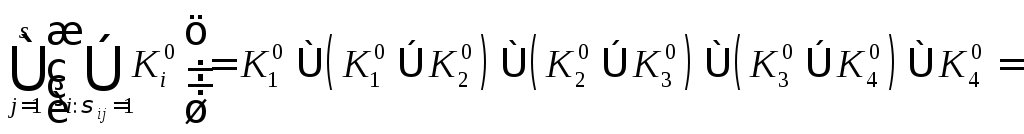2 Этап: построение тупиковых днф.
Приведем (без обоснования) алгоритм
построения тупиковых ДНФфункции
по совокупности ее простых импликантов.
Пусть
 - произвольная булева функция. Множество,
состоящее из булевых векторов, на которых
функция
- произвольная булева функция. Множество,
состоящее из булевых векторов, на которых
функция
 принимает значение 1, будем называтьносителем функции. Пусть булевы
вектора
принимает значение 1, будем называтьносителем функции. Пусть булевы
вектора - элементы носителя функции
- элементы носителя функции
 ,
, - совокупность простых импликант функции.
Составим таблицу, строки которой
соответствуют простым импликантам
функции, столбцы – элементам носителя,
а в ячейках на пересечении строки
- совокупность простых импликант функции.
Составим таблицу, строки которой
соответствуют простым импликантам
функции, столбцы – элементам носителя,
а в ячейках на пересечении строки и столбца
и столбца проставлено число
проставлено число
 ,
равное 1, если на наборе
,
равное 1, если на наборе простой импликант
простой импликант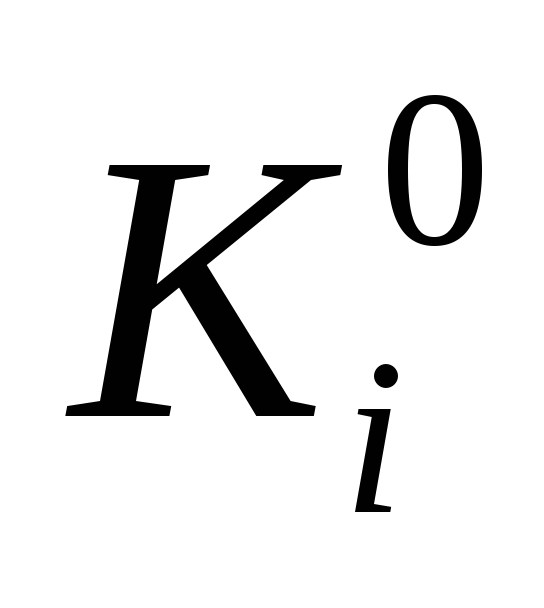 обращается в единицу, и равное 0 в
противном случае. Эта таблица называется
импликантной.
обращается в единицу, и равное 0 в
противном случае. Эта таблица называется
импликантной.
Cоставим выражение
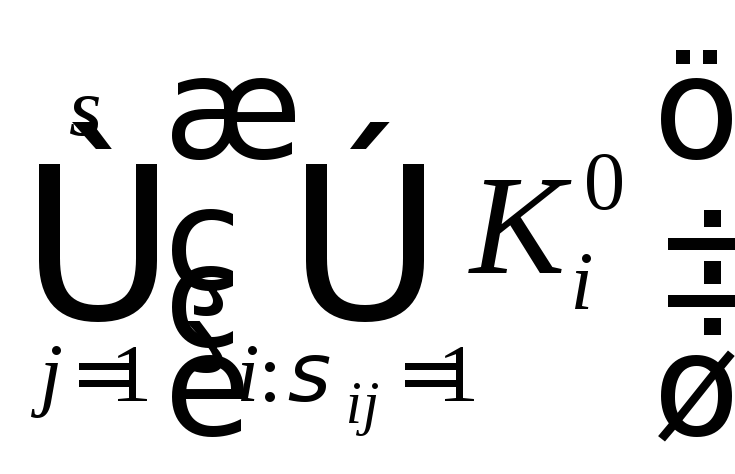
и произведем преобразование
 ,
рассматривая символы
,
рассматривая символы
 как булевы переменные. После этого в
полученном выражении ликвидируем
поглощаемые или дублируемые члены, т.е.
совершим преобразования вида
как булевы переменные. После этого в
полученном выражении ликвидируем
поглощаемые или дублируемые члены, т.е.
совершим преобразования вида
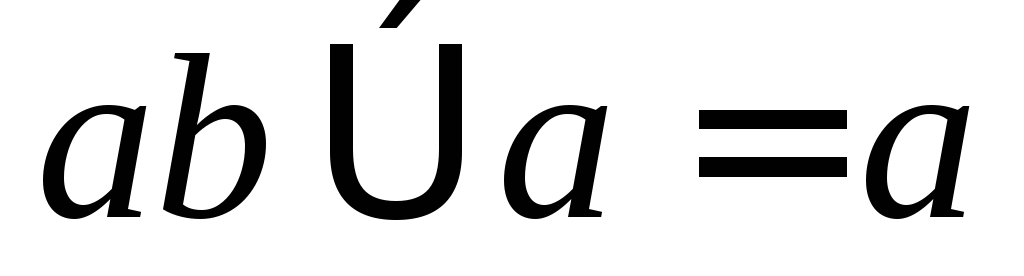 ,
,
 .
Каждое дизъюнктное слагаемое в упрощенном
выражении
.
Каждое дизъюнктное слагаемое в упрощенном
выражении
 будет определять тупиковую ДНФ, а именно:
каждое слагаемое представляет собой
произведение конъюнкций
будет определять тупиковую ДНФ, а именно:
каждое слагаемое представляет собой
произведение конъюнкций
 ;
дизъюнкция этих конъюнкций есть тупиковая
ДНФ функции.
;
дизъюнкция этих конъюнкций есть тупиковая
ДНФ функции.
Пример 5.
Следуя изложенному выше алгоритму,
найдем тупиковые ДНФ функции
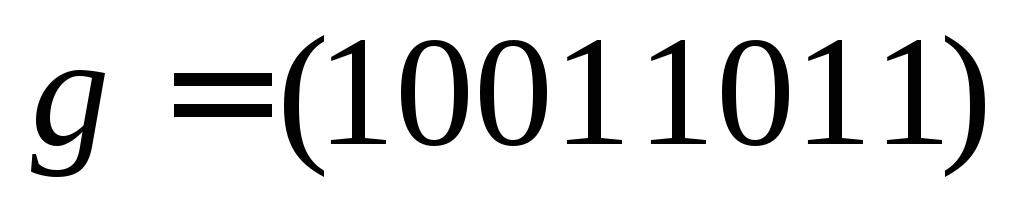 .
.
Совокупность простых импликант функции
 была найдена нами в ходе решения примера
2. Пусть
была найдена нами в ходе решения примера
2. Пусть
 ,
,
 ,
,
 ,
,
 .
Составим импликантную таблицу:
.
Составим импликантную таблицу:
|
|
000 |
100 |
110 |
111 |
011 |
|
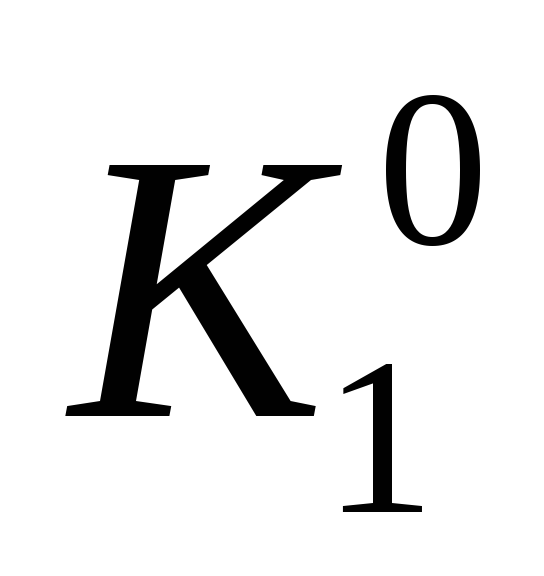
|
1 |
1 |
0 |
0 |
0 |
|
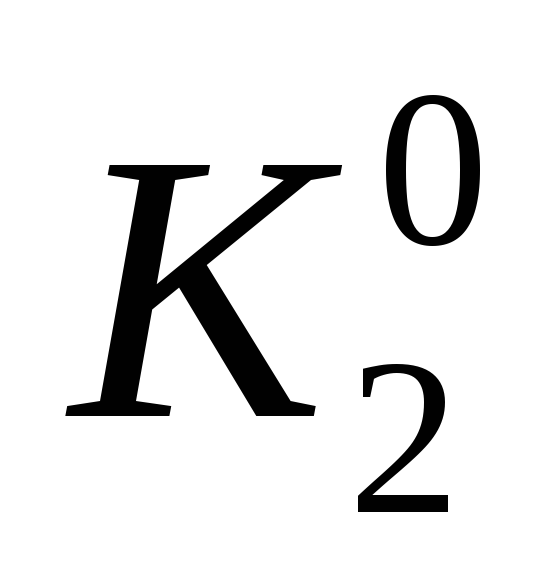 |
0 |
1 |
1 |
0 |
0 |
|
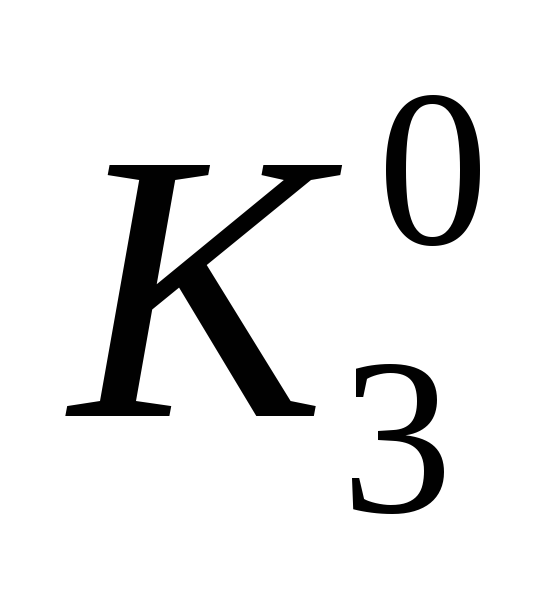
|
0 |
0 |
1 |
1 |
0 |
|
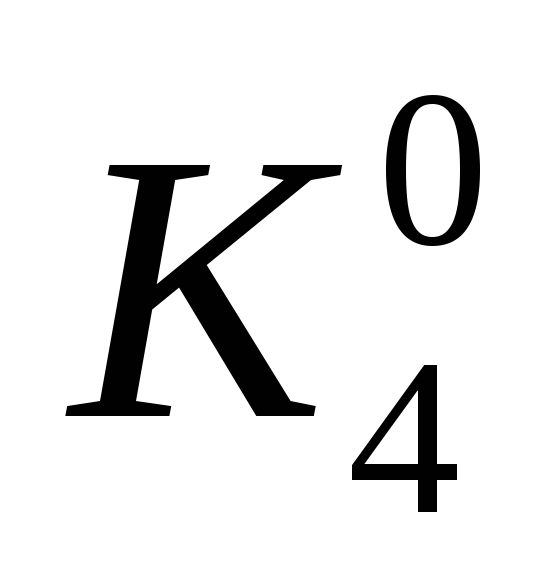
|
0 |
0 |
0 |
1 |
1 |
Тогда
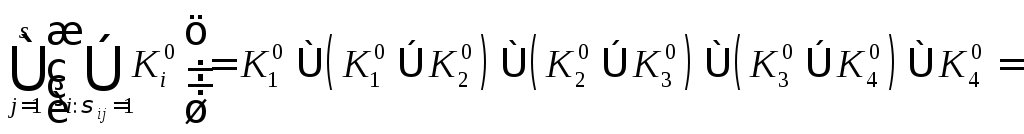
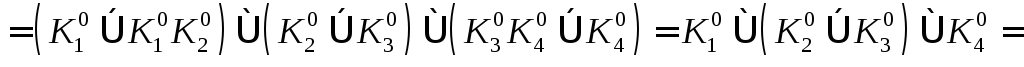
 .
.
Мы получаем две тупиковых ДНФ:
 и
и
 .
.
3 Этап: построение минимальных днф.
Согласно утверждению 3 минимальными
ДНФ функции будут ее тупиковые ДНФ
наименьшей сложности. Поэтому, после
того как все тупиковые ДНФ построены,
нам осталось выбрать из них минимальную
ДНФ.
Например, для
функции
 (см. пример 2) обе тупиковые ДНФ имеют
сложность, равную шести, и, следовательно,
обе являются минимальными.
(см. пример 2) обе тупиковые ДНФ имеют
сложность, равную шести, и, следовательно,
обе являются минимальными.
31