2.13. Представление булевых функций дизъюнктивными нормальными формами

Пусть задан алфавит переменных . Далее по умолчанию будем полагать, что.

Определение.Формулу вида (при ,) называют элементарной конъюнкцией ранга r над множеством X. Константа 1 рассматривается как элементарная конъюнкция ранга 0.

Например,формула- элементарная конъюнкция ранга 3 над множеством; в то время как формулаэлементарной конъюнкцией не является.

Определение.Формулу вида (при ), где черезобозначены элементарные конъюнкции над множеством X,называют дизъюнктивной нормальной формой (ДНФ) над множеством X. Сумма рангов конъюнкций, входящих в ДНФ, называется сложностью ДНФ.

Совершенная дизъюнктивная нормальная форма - одна из разновидностей ДНФ.

Пример 1.- ДНФ сложности 6;- ДНФ сложности 4;- ДНФ сложности 3 над множеством.

Заметим, что формулы равносильны и, следовательно, реализуют одну и ту же функциюh. Делаем вывод: функция может быть реализована в виде ДНФ не единственным образом, причем ДНФ, реализующие функцию, могут иметь различную сложность.

Определение.ДНФ, имеющая по сравнению с другими ДНФ, реализующими данную функцию, наименьшую сложность, называется минимальной дизъюнктивной нормальной формой данной функции.

Так, для функции h, реализуемой дизъюнктивными нормальными формами из примера 1, ДНФявляется минимальной, посколькуhзависит от переменныхсущественным образом и, значит, не может быть представлена ДНФ, содержащей менее трех букв.

Поставим задачу: построить для произвольной булевой функции минимальные ДНФ.

Заметим, что у этой задачи существует тривиальное решение. Дадим его пошаговое описание.

1. Строим все ДНФ над множеством . Их. Действительно, число различных элементарных конъюнкций равно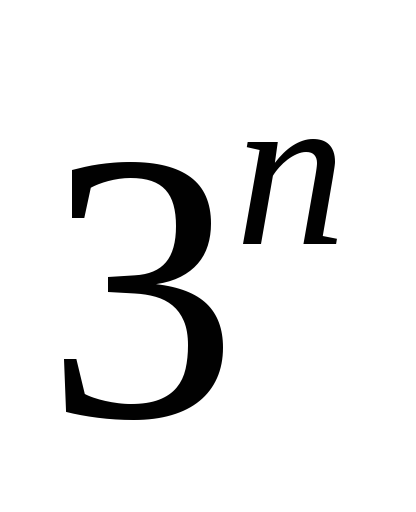, так как для каждой переменнойимеется три возможности: присутствовать в конъюнкции, присутствовать с отрицанием, и отсутствовать. Каждая из конъюнкций, в свою очередь, может либо входить, либо не входить в ДНФ.

2. Отбираем из построенных ДНФ те, которые реализуют функцию .

3. Для отобранных ДНФ определяем сложности; ДНФ наименьшей сложности и есть искомые минимальные ДНФ функции .

В силу большого объема операций пользоваться изложенным выше алгоритмом практически невозможно. Разработано несколько более экономичных методов построения минимальных ДНФ. Мы познакомимся с одним из них.

Нам понадобятся несколько новых понятий.

Определение.Элементарная конъюнкция называется импликантом функции , если на любом наборе , на котором эта элементарная конъюнкция равна 1, функциятакже обращается в 1.

Очевидно, что любая элементарная конъюнкция произвольной ДНФ, реализующей функцию , является ее импликантом.

Определение.Будем называть импликант функцииеепростым импликантом, если элементарная конъюнкция, получающаяся из него удалением любой буквы, уже не является импликантом .

Определение.Дизъюнкция всех простых импликантов функции называется сокращенной ДНФ функции.

Утверждение 1. Сокращенная ДНФ функцииреализует функцию.

Доказательство.Покажем, что значения сокращенной ДНФ функции и самой функции совпадают при любых значениях переменных.

Пусть на некотором наборе функция. Тогда некоторая элементарная конъюнкция СДНФ функции обращается в 1 на этом наборе. Некоторая часть этой элементарной конъюнкции будет простым импликантом функции .Этот простой импликант обращается в 1 на наборе, следовательно, и сокращенная ДНФ функции обратится на этом наборе в 1.

С другой стороны, если сокращенная ДНФ функции на наборе равна 1, то некоторая ее элементарная конъюнкцияравна 1 на этом наборе. Но конъюнкция- простой импликант функции , следовательно, на каждом наборе, на которомравна 1, тоже равна 1. Таким образом,. ■

Утверждение 2. Минимальная ДНФ функции является дизъюнкцией простых импликантов этой функции.

Доказательство.Будем рассуждать от противного. Предположим, что в минимальную ДНФ входит непростой импликант. Рассмотрим ДНФ, которая получается из минимальной ДНФ функции заменой этого непростого импликанта на простой, полученный из него опусканием некоторых букв. Полученная ДНФ будет содержать меньшее число букв и все еще реализовывать функцию (обоснуйте!), что противоречит предположению о минимальности исходной ДНФ.■

Определение.Реализующая функцию дизъюнкция ее простых импликантов называется тупиковой ДНФ функции, если из нее нельзя удалить ни один простой импликант так, чтобы полученная ДНФ все еще реализовала функцию.

Утверждение 3. Минимальная ДНФ функции является тупиковой ДНФ.

Доказательство.Будем рассуждать от противного. Предположим, что найдется минимальная ДНФ, которая не является тупиковой. Тогда из этой ДНФ можно удалить хотя бы один простой импликант так, чтобы образовавшаяся при этом новая ДНФ по-прежнему реализовала функцию. Но эта новая ДНФ будет иметь меньшую сложность, чем исходная минимальная ДНФ. А это противоречит тому, что сложность минимальной ДНФ - наименьшая из возможных.■

Теперь мы можем наметить план построения минимальной ДН функции. План будет включать три этапа: на первом этапе строится сокращенная ДНФ функции, на втором – тупиковые ДНФ, на третьем – из тупиковых отбираются минимальные.