Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / параграф 2

2.2. Реализация булевых функций формулами

Пусть - некоторое подмножество функций из ;

- множество символов, используемых для обозначения переменных (алфавит переменных);

- множество символов, используемых для обозначения функций из множества (алфавит функций).

Далее в этом параграфе по умолчанию будем полагать, что , .

Дадим индуктивное определение формулы над :

1. Базис индукции. Каждое выражение вида , где 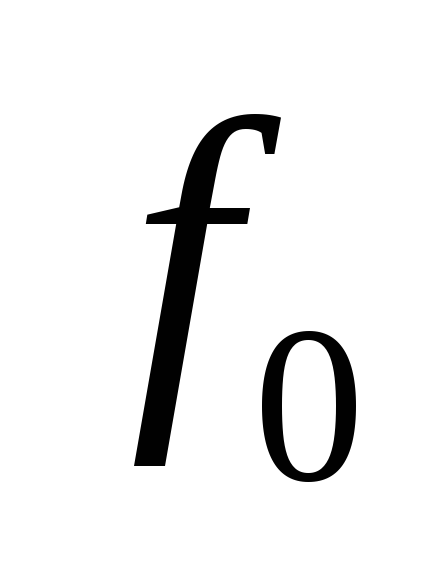- символ из , называется формулой над ;

2. Индуктивный переход. Выражение вида , где - либо символ переменной 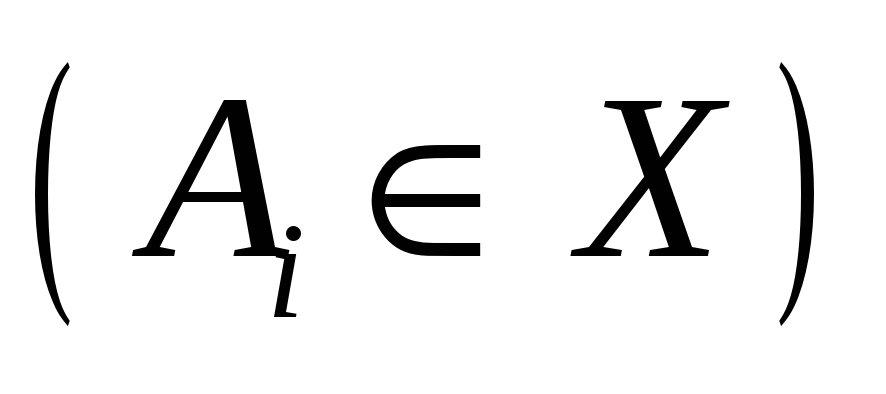, либо формула над , называется формулой над .

Для краткой записи формул используются такие обозначения:

- формула над множеством ;

- формула над множеством функций .

В том случае, когда нужно обратить внимание на множество переменных, которые участвуют в построении формулы, пишут .

Пример 1. - формулы над множеством элементарных функций.

Сопоставим каждой формуле над функцию по следующему индуктивному правилу:

1. Базис индукции. Если совпадает с , где , то формуле сопоставим функцию .

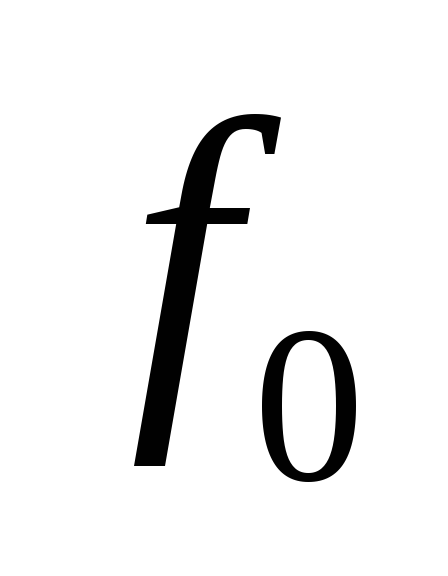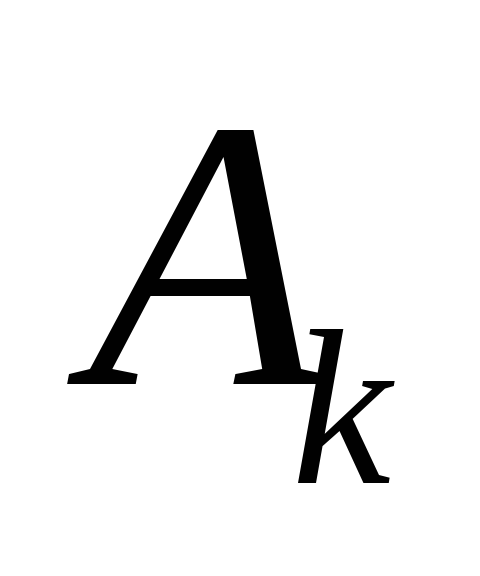
2. Индуктивный переход. Если формула совпадает с , где - символ функции из , - либо формула над , либо символ переменной , то тогда, по предположению индукции, в первом случае сопоставляется функция из , а во втором случае сопоставляется тождественная функция . Сопоставим формуле функцию 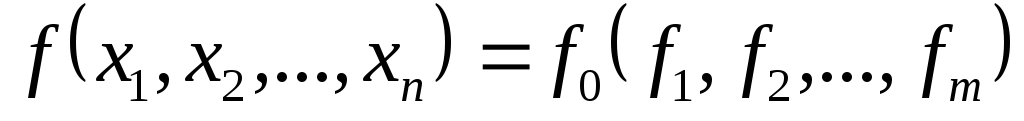; значение функции на каждом наборе находится как значение функции 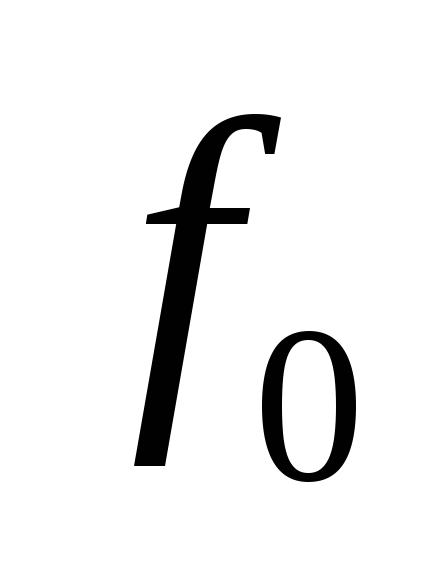на наборе .

Если функция сопоставлена формуле над , то говорят, то формула реализует функцию и пишут .

Функцию , реализуемую формулой над множеством функций , будем называть суперпозицией функций .

Пример 2. Формула реализует функцию , заданную таблицей истинности:

0	0	1	0	0
0	1	1	1	1
1	0	0	1	0
1	1	0	0	0

Пример 3. Формула реализует функцию , заданную таблицей истинности:

0	0	1	0
0	1	1	1
1	0	0	0
1	1	0	0

Заметим, что формулы и различны, а реализуемые ими функции и равны.

Если две формулы и реализуют равные функции, то они называются равносильными. Равносильность формул обозначают так: .

Замечание. Для упрощения записи формул введены следующие соглашения:

а) внешние скобки у формул можно опускать;

б) вместо можно писать , а вместо – или ;

в) связку принято считать сильнее любой двуместной связки, поэтому внешние скобки в выражении, над которым стоит знак « – », можно опускать;

г) связку принято считать сильнее и , поэтому выражения , , можно в скобки не брать.

Пример 4.

.

Теорема. Для формул над множеством имеют место следующие равносильности:

1. ;

2. ;

3.;

4. ;

5.;

6. ;

7. ; 8. ;

9. ; 10. ;

11. ; 12. ;

13. ; 14. ;

15. ; 16. ;

17.; 18. ;

19. .

Доказательство. Все равносильности можно доказать, действуя по одной схеме. Покажем, как можно рассуждать, на примере равносильности 10. Строим таблицы истинности функций, которые реализуются формулами, стоящими в левой и правой части доказываемого равенства.

0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	0

0	0	1	1	1
0	1	1	0	1
1	0	0	1	1
1	1	0	0	0

Как видим, формулы и реализуют равные функции и, следовательно, являются равносильными. ■

Дополним соглашение об упрощенной записи формул: в случае многократного применения ассоциативной операции скобки можно опускать. Например, формулу можно записать в виде . В дальнейшем будем также употреблять следующие обозначения: и .

Упражнение. Доказать, что имеют место равносильности:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

14