
Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / параграф 2.5-2
.8.doc2.5. Полнота системы булевых функций
Определение. Множество булевых
функций
![]() называется полной
системой, если любая булева функция
может быть реализована формулой над
называется полной
системой, если любая булева функция
может быть реализована формулой над
![]() .
.
Примеры. 1.
![]() - полная система.
- полная система.
2.
![]() - полная (см. утверждение параграфа 2.4).
- полная (см. утверждение параграфа 2.4).
Теорема (о полноте). Пусть
заданы две системы функций из
![]() :
:
![]() и
и
![]() .
Тогда, если система
.
Тогда, если система
![]() - полная и каждая ее функция может быть
реализована формулой над
- полная и каждая ее функция может быть
реализована формулой над
![]() ,
то система
,
то система
![]() тоже полная.
тоже полная.
Доказательство. Пусть
![]() - произвольная функция из
- произвольная функция из
![]() .
Покажем, что ее можно реализовать
формулой над
.
Покажем, что ее можно реализовать
формулой над
![]() .
.
В силу полноты
![]()
![]() реализуется формулой над
реализуется формулой над
![]() ,
т.е.
,
т.е.
![]() .
Кроме этого, по условию
.
Кроме этого, по условию
![]() реализуются формулами над
реализуются формулами над
![]() ,
т.е.
,
т.е.![]() .
Следовательно, в формуле
.
Следовательно, в формуле
![]() мы можем исключить вхождение символов
функций
мы можем исключить вхождение символов
функций
![]() ,
заменив их соответствующими формулами:
,
заменив их соответствующими формулами:
![]() .
.
Полученное выражение определяет формулу
над
![]() ,
реализующую
,
реализующую
![]() .
■
.
■
Примеры. 3.
Система
![]() -
полная. Действительно, рассмотрим
системы
-
полная. Действительно, рассмотрим
системы
![]() и
и
![]() .
Система
.
Система
![]() - полная и, поскольку
- полная и, поскольку
![]() ,
то каждая функция этой системы выражается
формулой над
,
то каждая функция этой системы выражается
формулой над
![]() .
Таким образом, условия теоремы о полноте
выполнены и, значит, система
.
Таким образом, условия теоремы о полноте
выполнены и, значит, система
![]() -
полная система.
-
полная система.
4. Система
![]() -
полная. Действительно, рассмотрим
системы
-
полная. Действительно, рассмотрим
системы
![]() и
и
![]() .
Имеем:
.
Имеем:
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
.
Таким образом, каждая функция системы
![]() реализуется формулой над
реализуется формулой над
![]() .
Кроме того, система
.
Кроме того, система
![]() - полная. Следовательно, условия теоремы
о полноте выполнены и, значит,
- полная. Следовательно, условия теоремы
о полноте выполнены и, значит,
![]() -
полная система.
-
полная система.
5. Система
![]() -
полная. Докажите это утверждение
самостоятельно.
-
полная. Докажите это утверждение
самостоятельно.
6. Система
![]() -
полная. Действительно, рассмотрим
системы
-
полная. Действительно, рассмотрим
системы
![]() и
и
![]() .
Система
.
Система
![]() - полная и, поскольку
- полная и, поскольку
![]() ,
то каждая функция этой системы выражается
формулой над
,
то каждая функция этой системы выражается
формулой над
![]() .
Таким образом, условия теоремы о полноте
выполнены и, значит, система
.
Таким образом, условия теоремы о полноте
выполнены и, значит, система
![]() -
полная система.
-
полная система.
2.6. Полином Жегалкина
Пусть M – некоторое
произвольное подмножество булевого
куба
![]() ,
,
![]() ,
,
![]() - номер вектора
- номер вектора
![]() ,
,
![]() - его вес,
- его вес,
![]() - номера отличных от нуля координат
вектора
- номера отличных от нуля координат
вектора
![]() .
.
Определение. Формула вида
![]() ,
(1)
,
(1)
где суммирование ведется по модулю
два, а коэффициенты
![]() равны либо 0, либо 1, называется полиномом
Жегалкина от
равны либо 0, либо 1, называется полиномом
Жегалкина от
![]() переменных.
переменных.
Если суммирование в формуле 1 ведется
по всем булевым векторам длины n,
слагаемые идут в порядке возрастания
номеров булевых векторов и
![]() ,
то говорят, что полином Жегалкина записан
в канонической форме.
,
то говорят, что полином Жегалкина записан
в канонической форме.
Запишем для примера общий вид канонической
формы полинома Жегалкина от 2-х переменных:
![]() ;
;
от 3-х переменных:
![]()
Замечание.
Каждый полином Жегалкина от n
можно записать в канонической форме.
Например, полином
Жегалкина от двух переменных
![]() в канонической форме запишется так:
в канонической форме запишется так:
![]()
Теорема. Каждая булева функция
от
![]() переменных может быть реализована в
виде канонического полинома Жегалкина
от
переменных может быть реализована в
виде канонического полинома Жегалкина
от
![]() переменных, причем единственным образом.
переменных, причем единственным образом.
Доказательство. 1. Докажем
возможность реализации. Пусть
![]() .
Так как система
.
Так как система
![]() - полная (пример 6 параграфа 2.5), то
- полная (пример 6 параграфа 2.5), то
![]() может быть реализована формулой над
может быть реализована формулой над
![]() ,
т.е.
,
т.е.
![]() .
.
В формуле
![]() совершим ряд преобразований: раскроем
скобки, воспользовавшись дистрибутивностью
операций сложения по модулю два и
конъюнкции, после чего полученные
формулы упростим, используя тождества
совершим ряд преобразований: раскроем
скобки, воспользовавшись дистрибутивностью
операций сложения по модулю два и
конъюнкции, после чего полученные
формулы упростим, используя тождества
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
В результате придем к полиному Жегалкина,
который можем записать в каноническом
виде.
.
В результате придем к полиному Жегалкина,
который можем записать в каноническом
виде.
2. Докажем единственность реализации.
Каждый канонический полином Жегалкина
от
![]() переменных однозначно определяется
набором своих коэффициентов
переменных однозначно определяется
набором своих коэффициентов
![]() .
Каждый такой набор можно рассматривать
как булев вектор длины
.
Каждый такой набор можно рассматривать
как булев вектор длины
![]() .
Следовательно, канонических полиномов
Жегалкина от
.
Следовательно, канонических полиномов
Жегалкина от
![]() переменных столько же, сколько булевых
векторов длины
переменных столько же, сколько булевых
векторов длины
![]() ,
т.е.
,
т.е.
![]() .
Таким образом, число канонических
полиномов Жегалкина от
.
Таким образом, число канонических
полиномов Жегалкина от
![]() переменных совпадает с числом функций
от
переменных совпадает с числом функций
от
![]() переменных.
переменных.
Предположим теперь, что представление
некоторых функций в виде канонического
полинома Жегалкина не единственно.
Поскольку число булевых функций
![]() переменных и число канонических полиномов
Жегалкина от
переменных и число канонических полиномов
Жегалкина от
![]() переменных одинаково, то из неоднозначности
представления следует, что найдется
канонический полином Жегалкина,
реализующий не менее двух функций, что
невозможно. Пришли к противоречию,
следовательно, наше предположение было
неверным.
■
переменных одинаково, то из неоднозначности
представления следует, что найдется
канонический полином Жегалкина,
реализующий не менее двух функций, что
невозможно. Пришли к противоречию,
следовательно, наше предположение было
неверным.
■
Для нахождения полинома Жегалкина,
реализующего функцию
![]() ,
применяют два способа: метод неопределенных
коэффициентов и метод равносильных
преобразований.
,
применяют два способа: метод неопределенных
коэффициентов и метод равносильных
преобразований.
Метод неопределенных коэффициентов
состоит в следующем. Пусть функция
![]() зависит от
зависит от
![]() переменных. В общем виде записывают
канонический полином Жегалкина
переменных. В общем виде записывают
канонический полином Жегалкина
![]() от
от
![]() переменных. Для каждого набора
переменных. Для каждого набора
![]() значений переменных составляют уравнение
значений переменных составляют уравнение
![]() .
.
В результате получают систему из
![]() уравнений, которая однозначно определяет
коэффициенты полинома.
уравнений, которая однозначно определяет
коэффициенты полинома.
Примеры.
1. Найти полином Жегалкина, реализующий
функцию
![]() .
.
Зададим функцию
![]() таблично:
таблично:
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Воспользуемся методом неопределенных
коэффициентов. Канонический полином
Жегалкина от двух переменных имеет вид:
![]() .
Поэтому должны выполняться равенства:
.
Поэтому должны выполняться равенства:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Откуда
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Тот же результат можно получить проще,
если действовать методом равносильных
преобразований:
![]() .
.
2. Найти полином Жегалкина, реализующий
функцию
![]() .
.
![]()
![]() .
.
2.7. Замыкание системы булевых функций.
Определение. Пусть
![]() - некоторое подмножество
- некоторое подмножество
![]() .
Множество всех булевых функций,
реализуемых формулой над
.
Множество всех булевых функций,
реализуемых формулой над
![]() ,
называется замыканием
,
называется замыканием
![]() и обозначается
и обозначается
![]() .
.
Пример. Пусть
![]() ,
тогда
,
тогда
![]() .
.
Операцию получения множества
![]() из
из
![]() называют операцией замыкания.
называют операцией замыкания.
Утверждение. Операция замыкания обладает следующими свойствами:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() .
.
Утверждение докажите самостоятельно.
Определение.
Класс
(множество) булевых функций
![]() называется замкнутым,
если
называется замкнутым,
если
![]() .2.8.
Классы
.2.8.
Классы
![]() и
и
![]() ,
их
свойства
,
их
свойства
Определение. Говорят, что булева
функция сохраняет
0, если
![]() .
.
Обозначим через
![]() множество функций от
множество функций от
![]() переменных, сохраняющих 0, а через
переменных, сохраняющих 0, а через
![]() – множество всех булевых функций,
сохраняющих 0, т.е.
– множество всех булевых функций,
сохраняющих 0, т.е.
![]() .
.
Например,
![]() ;
;
![]() .
.
Утверждение 1. Множество функций, сохраняющих 0, - замкнутый класс.
Доказательство. Наша задача
показать, что
![]() .
Согласно первому свойству операции
замыкания
.
Согласно первому свойству операции
замыкания
![]() .
Докажем, что и
.
Докажем, что и
![]() ,
т.е., что любая булева функция, реализованная
формулой над
,
т.е., что любая булева функция, реализованная
формулой над
![]() ,
сохраняет 0. Поскольку класс
,
сохраняет 0. Поскольку класс
![]() содержит тождественную функцию, нам
достаточно показать, что функция
содержит тождественную функцию, нам
достаточно показать, что функция
![]() ,
если
,
если
![]() .
.
Имеем,
![]() =
=![]()
![]() .
■
.
■
Лемма
![]() (о функции, не сохраняющей 0). Пусть
(о функции, не сохраняющей 0). Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать либо константу 1, либо
отрицание.
можно реализовать либо константу 1, либо
отрицание.
Доказательство. Пусть
![]() ,
т.е.
,
т.е.
![]() .
Рассмотрим функцию
.
Рассмотрим функцию
![]() .
.
Возможны два случая:
![]() или
или
![]() .
.
В первом случае:
![]()
![]() .
.
Во втором случае:
![]()
![]() .
■
.
■
В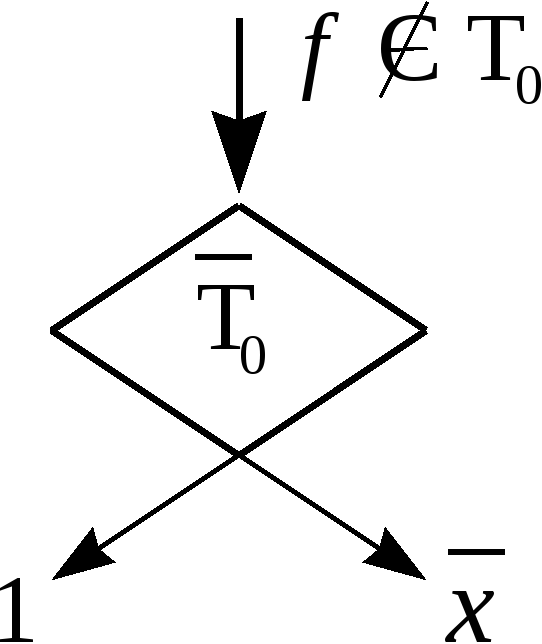 ведем
условное обозначение алгоритма,
использованного для доказательства
леммы
ведем
условное обозначение алгоритма,
использованного для доказательства
леммы![]() :
:
Определение. Говорят, что булева
функция сохраняет
1, если
![]() .
.
Обозначим через
![]() множество функций от
множество функций от
![]() переменных, сохраняющих 1, а через
переменных, сохраняющих 1, а через
![]() – множество всех булевых функций,
сохраняющих 1, т.е.
– множество всех булевых функций,
сохраняющих 1, т.е.
![]() .
.
Например,
![]() ;
;
![]() .
.
Утверждение 2. Множество функций, сохраняющих 1, - замкнутый класс.
Доказательство. Наша задача
показать, что
![]() .
Согласно первому свойству замыкания
.
Согласно первому свойству замыкания
![]() .
Докажем, что и
.
Докажем, что и
![]() ,
т.е., что любая булева функция, реализованная
формулой над
,
т.е., что любая булева функция, реализованная
формулой над
![]() ,
сохраняет 1. Поскольку класс
,
сохраняет 1. Поскольку класс
![]() содержит тождественную функцию, нам
достаточно показать, что функция
содержит тождественную функцию, нам
достаточно показать, что функция
![]() ,
если
,
если
![]() .
.
Имеем:
![]()
![]()
![]() .
■
.
■
Лемма
![]() (о функции, не сохраняющей 1). Пусть
(о функции, не сохраняющей 1). Пусть
![]() .
Тогда формулой над множеством
.
Тогда формулой над множеством
![]() можно реализовать либо константу 0, либо
отрицание.
можно реализовать либо константу 0, либо
отрицание.
Доказательство. Пусть
![]() ,
т.е.
,
т.е.
![]() .
Рассмотрим функцию
.
Рассмотрим функцию
![]() .
.
Возможны два случая:
![]() или
или
![]() .
.
В первом случае:
![]()
![]() .
.
Во втором случае:
![]()
![]() .
■
.
■
Введем условное обозначение алгоритма,
использованного для доказательс тва
леммы
тва
леммы![]() :
:
Упражнения. 1.
Выяснить, сколько имеется булевых
функций от
![]() переменных, сохраняющих 0.
переменных, сохраняющих 0.
Решение. Пусть
![]() .
Тогда
.
Тогда
 .
Следовательно,
булевых функций от
.
Следовательно,
булевых функций от
![]() переменных, сохраняющих 0, столько,
сколько и булевых векторов длины
переменных, сохраняющих 0, столько,
сколько и булевых векторов длины
![]() ,
т.е.
,
т.е.
![]() .
.
2. Выяснить,
сколько имеется булевых функций от
![]() переменных, сохраняющих 1.
переменных, сохраняющих 1.
3. Рассмотреть
работу леммы
![]() на примере функции
на примере функции
![]() .
.
4. Рассмотреть
работу леммы
![]() на примере функции
на примере функции
![]() .
.
