Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / параграф 2.10-11

2.10. Класс монотонных функций и его свойства

Определение. Если для любого (), то говорят, что вектор предшествует вектору и пишут .

Например, ; .

Определение. Говорят, что булева функция монотонна, если для любых наборов и значений переменных, таких что , выполняется неравенство .

Обозначим через множество монотонных функций от переменных, а через – множество всех монотонных функций; т.е. .

Например, ; .

Утверждение. Множество монотонных функций - замкнутый класс.

Доказательство. Наша задача показать, что . Согласно первому свойству операции замыкания . Докажем, что и , т.е., что любая булева функция, реализованная формулой над , монотонна. Поскольку класс содержит тождественную функцию, нам достаточно показать, что функция , если .

Возьмем два произвольных набора значений переменных и таких, что . Тогда, в силу монотонности функций , будем иметь:

,

,

………………………………………………………

.

Следовательно, , и, в силу монотонности , . Или

Таким образом, , что и требовалось доказать. ■

Лемма (о немонотонной функции). Пусть . Тогда формулой над множеством можно реализовать отрицание.

Доказательство. Пусть . Тогда существуют такие наборы и значений переменных, что

,

а

.

И, значит,

, . (1).

Поскольку , то можно выделить подпоследовательность индексов такую, что: и для всякого (и, значит, ).

Рассмотрим функцию , реализуемую формулой, получающейся в результате подстановки в формулу на места чисел соответственно, а на остальные места - . Не ограничивая общности рассуждений, можно считать, что

.

Тогда

;.

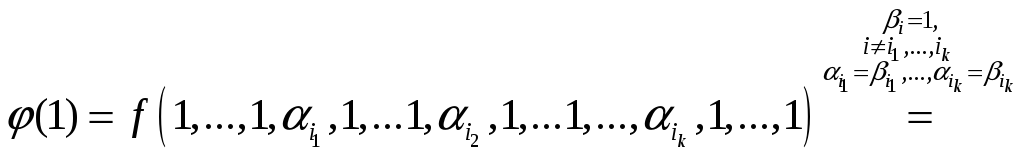
Следовательно, . ■

В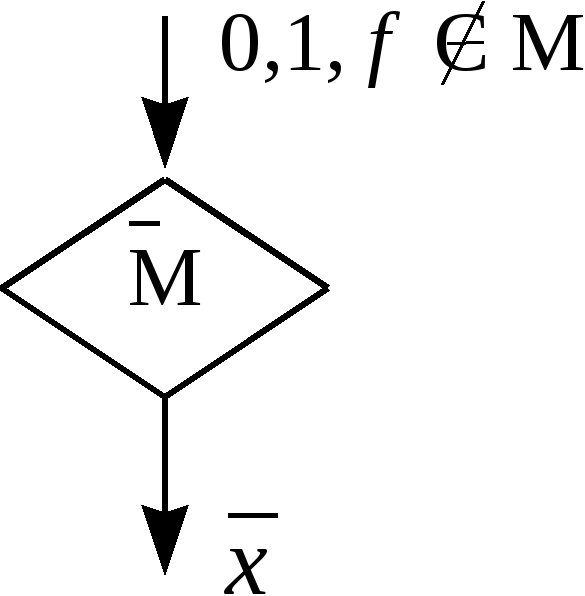ведем условное обозначение алгоритма, использованного для доказательства леммы :

Упражнение. Рассмотреть «работу» леммы на примере функции .

Решение. Для удобства рассуждений зададим функцию таблично, а также реализуем в виде СКНФ:

.

0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Заметим, что , но , следовательно, . В качестве набора возьмем набор , а набора - . У этих наборов первые координаты различны, а вторые и третьи совпадают, поэтому, следуя лемме, . Или .

2.11. Класс линейных функций и его свойства

Определение. Говорят, что булева функция линейна, если в ее каноническом полиноме Жегалкина коэффициенты при всех слагаемых, содержащих произведения переменных, равны 0.

Обозначим через множество линейных функций от переменных, а через – множество всех линейных булевых функций, т.е. .

Например, ; .

Утверждение. Множество линейных функций - замкнутый класс.

Доказательство. Наша задача доказать, что . Согласно первому свойству замыкания . Докажем, что и , т.е., что любая булева функция, реализованная формулой над , линейна. Поскольку класс содержит тождественную функцию, то нам достаточно показать, что функция , если .

Пусть

……………………………………….

.

Подставим правые части этих равенств в формулу для :

. ■

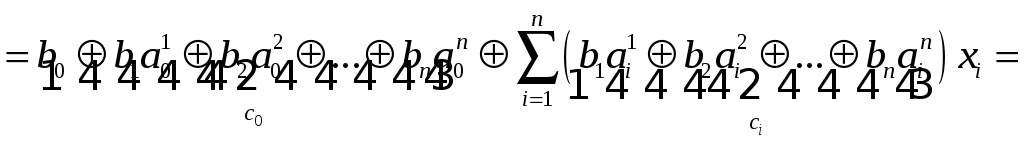
Лемма (о нелинейной функции). Пусть . Тогда формулой над множеством можно реализовать конъюнкцию.

Доказательство. Пусть . Тогда в каноническом полиноме Жегалкина данной функции найдется член с отличным от нуля коэффициентом, содержащий произведения переменных. Не нарушая общности рассуждений, можно считать, что этот член содержит . Следовательно, полином Жегалкина функции можно преобразовать к виду

,

где функция такова, что найдется набор значений переменных такой, что .

Рассмотрим функцию . Или

.

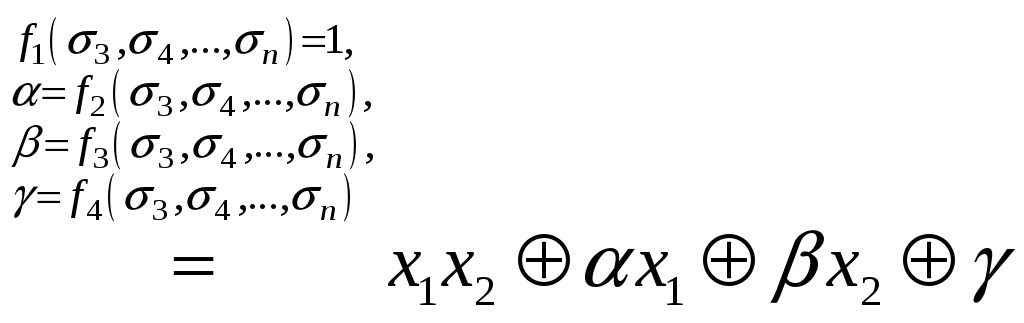Теперь перейдем к функции

.

Преобразуем формулу, реализующую функцию :

.

Подытоживая проделанное, можем записать

.

Заметим, что

Таким образом, можно утверждать, что конъюнкция реализована формулой над множеством . ■

Введем условное обозначение алгоритма, использованного для доказательства леммы :

Упражнения. 1. Выяснить, сколько имеется линейных булевых функций от переменных.

2. Рассмотреть работу леммы на примере функции .

Решение. Запишем полином Жегалкина функции в виде:

.

Поскольку при , то, следуя лемме, рассмотрим функцию

.

И, наконец, перейдем к функции

. ■

25