Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 2 / Введение к главе 2

Глава 2. Булева алгебра

Введение. Логика высказываний и логика предикатов

Любая научная теория воспринимается нами как некоторая система понятий и утверждений. Истинность каждого утверждения нуждается в доказательстве, которое в математике проводится с использованием логических средств. Именно эти логические средства изучает раздел математики, называемый математической логикой. Исходным понятием математической логики является понятие высказывания.

Под высказыванием принято понимать повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.

Например, предложение «» - истинное высказывание. Предложение «» - ложное высказывание. Предложения «» и «Студенты, ходите на лекции!» высказываниями не являются.

В математической логике интересуются не содержанием высказывания, а его истинностным значением, т.е. его истинностью или ложностью. Для истинностных значений будем использовать следующие обозначения: «1» для истинности и «0» для ложности.

Введем в рассмотрение основные логические связки:

Название	Прочтение	Обозначение
Отрицание	не
Конъюнкция	и
Дизъюнкция	или
Импликация	если … то
Эквиваленция	тогда и только тогда, когда

Используя логические связки, из одного или двух высказываний можно образовать новое высказывание, осуществив тем самым логическую операцию. При этом истинностные значения образованных высказываний определяются только истинностными значениями составляющих их высказываний, а не их смыслом.

Пусть и высказывания. Введем основные логические операции над высказываниями.

Название	Обозначение	Прочтение	Когда высказывание, полученное в результате операции, истинно	Когда высказывание, полученное в результате операции, ложно
Отрицание	()	не	если ложно	если истинно
Конъюнкция и		и	и оба истинны	в остальных случаях
Дизъюнкция и		или	в остальных случаях	и оба ложны
Импликация и		если , то ( влечет , из следует )	в остальных случаях	истинно, ложно
Эквиваленция и		тогда и только тогда когда ( эквивалентно )	и имеют одинаковые значения истинности	в остальных случаях

Операции удобно задавать с помощью таблиц истинности.

0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Высказывательными переменными будем называть такие переменные, значениями которых могут быть любые высказывания. Обозначать высказывательные переменные будем заглавными буквами латинского алфавита и так далее.

Введем, кроме того, две специфические высказывательные переменные И и Л. Множество значений переменной И ограничим истинными высказываниями, а множество значений переменной Л - ложными высказываниями.

Определение. Понятие формулы алгебры высказываний определим индуктивно следующими соглашениями:

1. Каждая отдельно взятая высказывательная переменная есть формула.

2. Если и 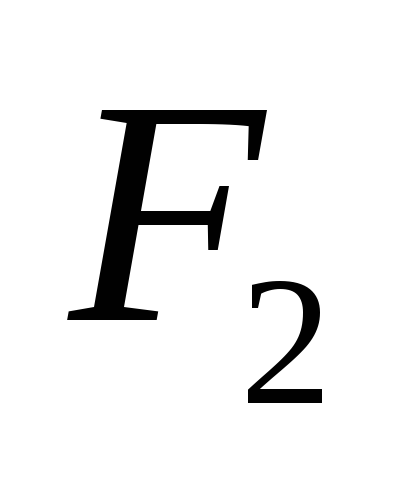- две формулы, то выражения , , 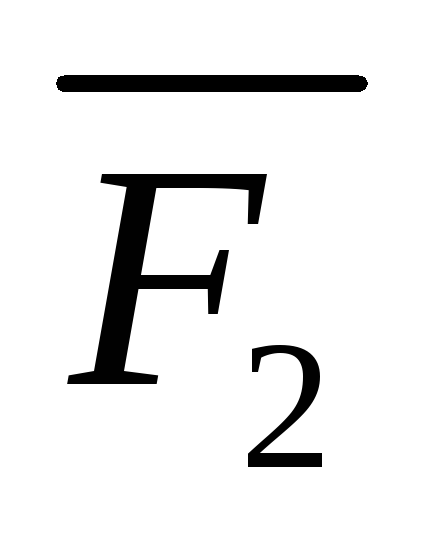, , 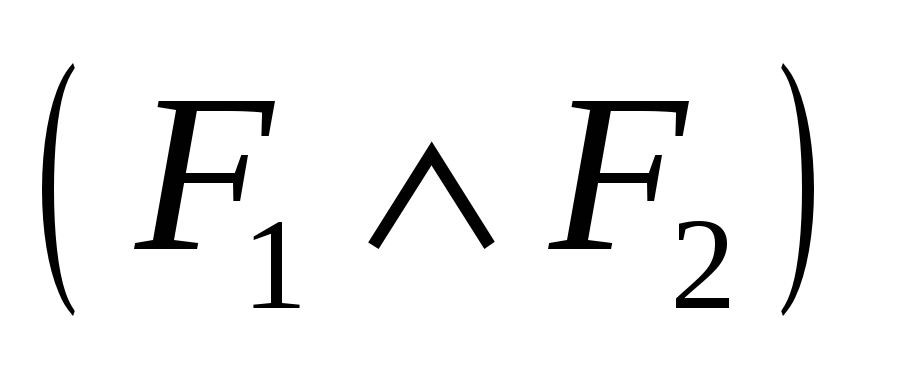, 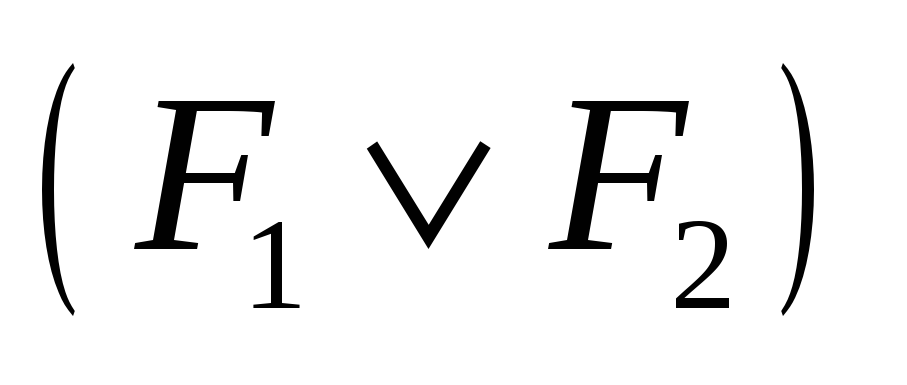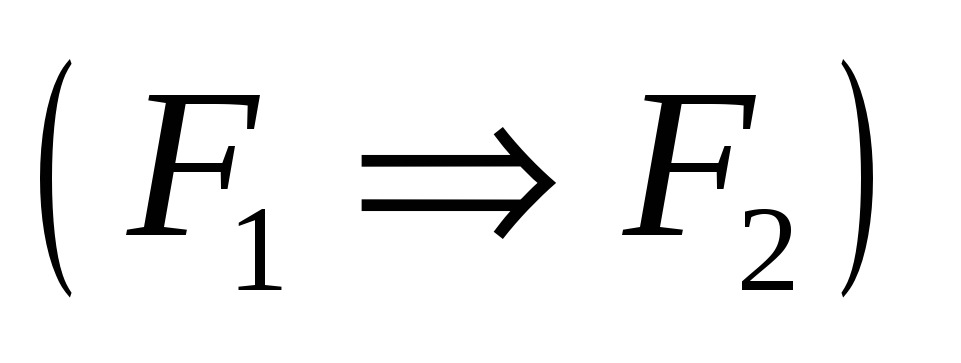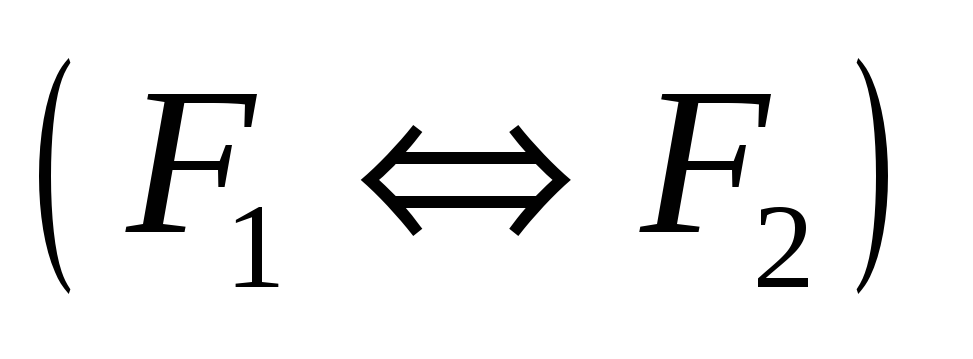также являются формулами.

3. Не существует никаких других формул, кроме тех, которые получаются в результате применения конечного числа раз пп. 1 и 2.

Например, формулами являются следующие выражения: , .

Запись внешних скобок у формулы будем считать необязательным, если только эта формула не входит составной частью в более сложную формулу.

Для каждой формулы можно составить таблицу истинности, т.е. таблицу, дающую значение истинности формулы в зависимости от значений истинности входящих в нее переменных.

Пример 1. Составить таблицу истинности формулы

.

0	0	1	1	1	1	1
0	1	1	0	1	1	1
1	0	0	1	0	0	1
1	1	1	0	0	1	1

Таким образом, значение истинности данной формулы равно 1 при любых значениях истинности высказывательных переменных. Формулы, обладающие таким свойством, называются тавтологиями.

Упражнение. Показать, что следующие формулы являются тавтологиями:

1. .

2. .

Значение тавтологий состоит, в частности, в том, что они дают правильные способы умозаключений. Например, схема логического умозаключения, выражаемого тавтологией , часто используется в математике и носит название «доказательство от противного».

Определение. Две формулы и алгебры высказываний называются равносильными, если при любых значениях истинности переменных истинностные значения высказываний и совпадают.

То, что формулы и равносильны, обозначают так: .

Пример 2. Доказать равносильность формул и .

Для каждой из данных формул составим таблицу истинности:

0	0	1
0	1	1
1	0	0
1	1	1

0	0	1	1
0	1	1	1
1	0	0	0
1	1	0	1

Сравнивая таблицы, видим, что указанные формулы равносильны.

Существует связь между понятием тавтологии и понятием равносильности формул. Она заключается в следующем: формулы и равносильны тогда и только тогда, когда формула является тавтологией.

Утверждение. Пусть - произвольные высказывания. Имеют место равносильности:

1. ;

2. ;

3.;

4. ;

5.;

6. ;

7. ; 8. ;

9. ; 10. ;

11. ; 12. ;

13. ; 14. ;

15. ; 16. ;

17. ; 18. ;

19. .

В качестве упражнения рекомендуем самостоятельно доказать перечисленные равносильности, взяв за образец решение примера 2.

Определение. Предложение, в которое входят переменных и которое при замене переменных возможными для них значениями становится высказыванием, называется -местным предикатом ().

При задании предиката обязательно указывается множество возможных значений переменных; это множество называется областью определения предиката.

Заметим, что 0 - местный предикат является высказыванием.

В дальнейшем одноместные предикаты с переменной будем обозначать через , и т.д., с двумя переменными , - через , и т.д., -местный предикат с переменными - через . Однако часто пишут просто , .

Пусть - -местный предикат с областью определения .

Подмножество множества , состоящее из тех значений переменных, при которых данный предикат превращается в истинное высказывание, называется областью истинности предиката и обозначается .

Подмножество множества , состоящее из тех значений переменных, при которых данный предикат превращается в ложное высказывание, называется областью ложности предиката и обозначается .

Пример 3. Предложение «, где является действительным числом» является одноместным предикатом, определенным на множестве действительных чисел. Его множество истинности состоит из двух чисел и . Следовательно, обозначив данный предикат через , можем записать: и .

Предикат с областью определения называют тождественно истинным, если при любых значениях переменных из он превращается в истинное высказывание.

Предикат с областью определения называют тождественно ложным, если при любых значениях переменных из он превращается в ложное высказывание.

Предикаты и , определенные на одном множестве , называются равносильными, если их множества истинности совпадают. Равносильность предикатов и обозначается так: .

Пример 4. Предикат : «» с областью определения равносилен предикату : «» с той же областью определения, поскольку .

Определение. Пусть и - два предиката с общей областью определения . Говорят, что есть следствие , если .

Пример 5. Предикат : «» с областью определения есть следствие предиката : «» с той же областью определения, поскольку .

Пусть - предикат с областью определения и - предикат с областью определения . Введем основные логические операции над предикатами. Результатом каждой такой логической операции над предикатом (в случае унарной операции) или предикатами и (в случае бинарной операции) является новый предикат, определенный следующим образом.

Название	Обозначение	Прочтение	Область определения предиката, полученного в результате операции	Множество истинности предиката, полученного в результате операции
Отрицание	()	не
Конъюнкция и		и
Дизъюнкция и		или
Импликация и		если , то ( влечет , из следует )
Эквиваленция и		тогда и только тогда когда ( эквивалентно )