Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 3 / параграф 3.17

3.17. Задача о максимальном потоке

В этом параграфе будут рассматриваться сети , имеющие единственную вершину с нулевой полустепенью захода и единственную вершину с нулевой полустепенью исхода. Вершину будем называть источником, а вершину - стоком сети . Вес дуги будем называть пропускной способностью этой дуги.

Для удобства изложения введем следующие обозначения. Через обозначим множество дуг, для которых вершина является началом, а через обозначим множество дуг, для которых вершина является концом.

Определение. Потоком в сети называется функция , удовлетворяющая условиям:

1. ;

2. для всех вершин , , , где и .

Значение можно интерпретировать как поток, втекающий в вершину , а значение - как поток, вытекающий из вершины . Тогда второе условие можно переформулировать так: поток, втекающий в любую вершину, за исключением источника и стока, должен быть равен вытекающему из этой вершины потоку.

Условие 1) называется условием ограничения по пропускной способности, а условие 2) – условием сохранения потока в вершинах.

Пример 1. На рисунке дан пример сети и потока в ней. Пропускная способность дуги указана около соответствующей дуги, там же через запятую указано значение .

Определение. Положим . Число называется величиной потока.

Определение. Поток называется максимальным, если для любого потока справедливо неравенство .

Задача о максимальном потоке состоит в следующем: в заданной сети найти поток максимальной величины.

Задача о максимальном потоке имеет одну особенность, отличающую ее от рассмотренных нами ранее задач дискретной оптимизации. В предшествующих задачах искомый объект существовал очевидным образом и в принципе мог быть найден полным перебором. Например, можно было перебрать все остовы и выбрать среди них минимальный или перебрать все пути между заданными вершинами и выбрать среди них кратчайший. В задаче о максимальном потоке полный перебор принципиально невозможен и существование максимального потока не является очевидным. Тем не менее, справедлива следующая теорема, которую мы приведем без доказательства.

Теорема. В каждой сети существует максимальный поток.

Определение. Цепью из вершины в вершину на сети называется последовательность попарно различных вершин и дуг

,

(здесь ), в которой любые два соседних элемента инцидентны.

Если при этом дуга выходит из вершины и заходит в вершину , то она называется прямой дугой цепи. Если же дуга выходит из вершины и заходит в вершину , то она называется обратной дугой цепи.

Пусть - поток в сети и - цепь из в . Для каждой дуги цепи положим

и

.

Определение. Цепь из в называется - дополняющей, если .

Пример 2. В сети, изображенной на рисунке 1, цепь, включающая последовательно вершины , является - дополняющей для потока, рассмотренного в примере 1.

Одним из алгоритмов, позволяющих построить максимальный поток, является алгоритм Форда-Фалкерсона.

Алгоритм Форда –Фалкерсона. 0-ой шаг. Положим для всех дуг .

-ый шаг. Пусть к началу шага по цепи течет поток . Для текущего потока ищется -дополняющая -цепь.

Если такой цепи нет, то максимальный поток найден: это .

В противном случае, если такая -дополняющая -цепь имеется, ей дается имя и по следующему правилу строится поток :

Величина этого потока определяется равенством

.

Замечание. Возникает существенный вопрос: закончится ли работа алгоритма за конечное число шагов? Оказывается, гарантии этому нет. Гарантировать построение максимального потока можно в случае, если на каждом шаге производить увеличение потока вдоль кратчайших по числу дуг -дополняющих цепей.

Пример 3. Построим максимальный поток для сети из примера 1.

Ш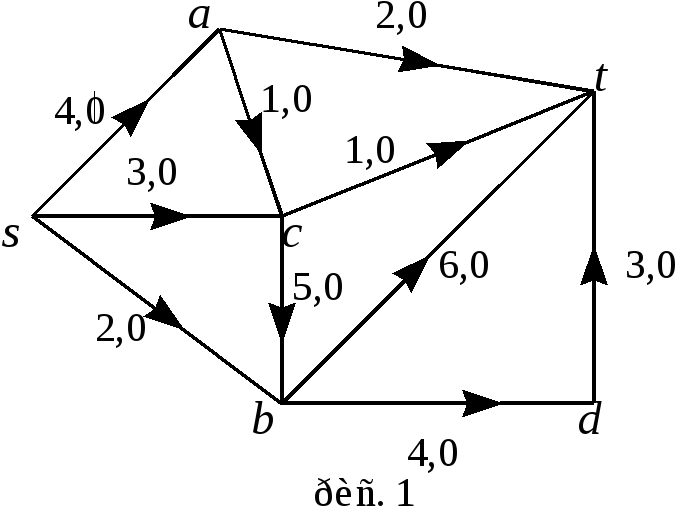аг 0. ;

поток указан на рис. 1;

.

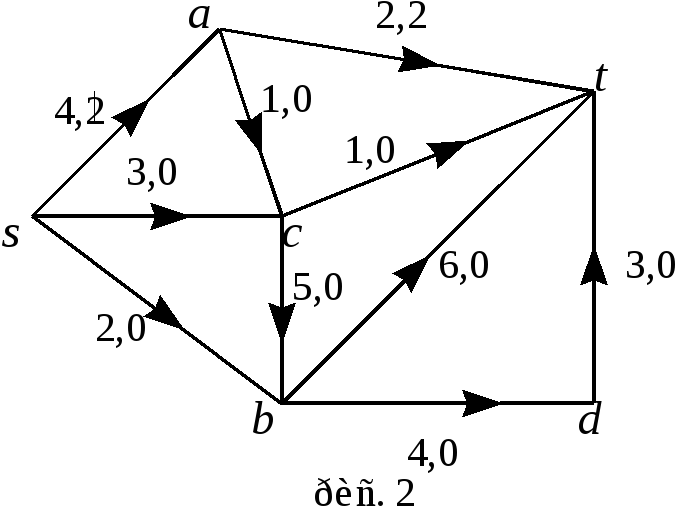
Шаг 1. ,

,

поток указан на рис. 2;

.

Ш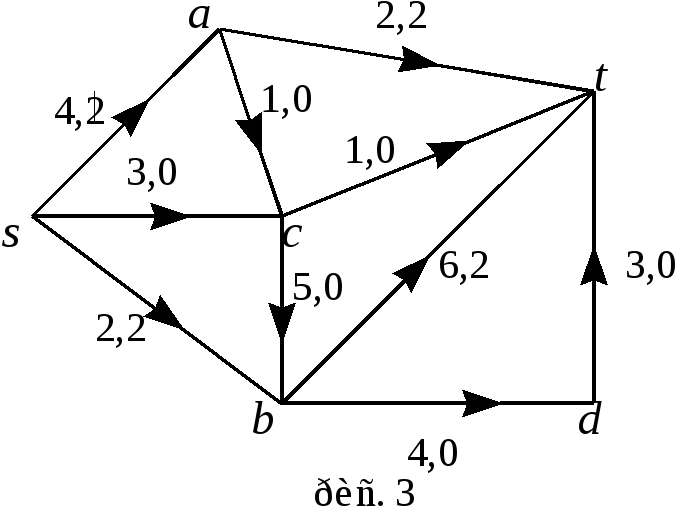аг 2. ,

,

поток указан на рис. 3;

.

Ш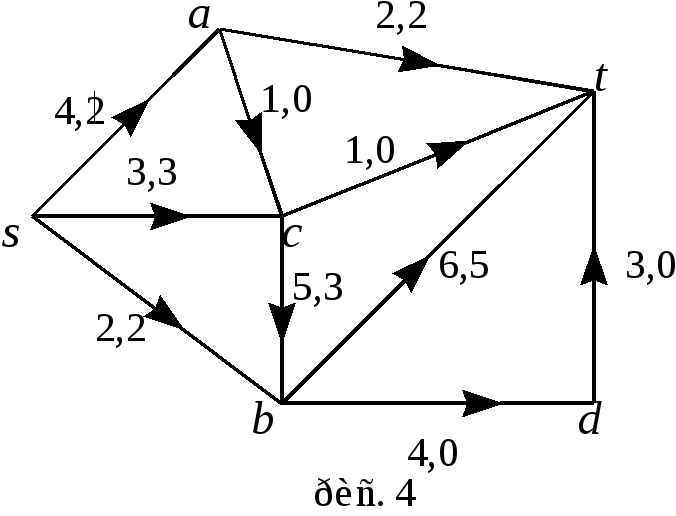аг 3. ,

,

поток указан на рис. 4;

.

Ш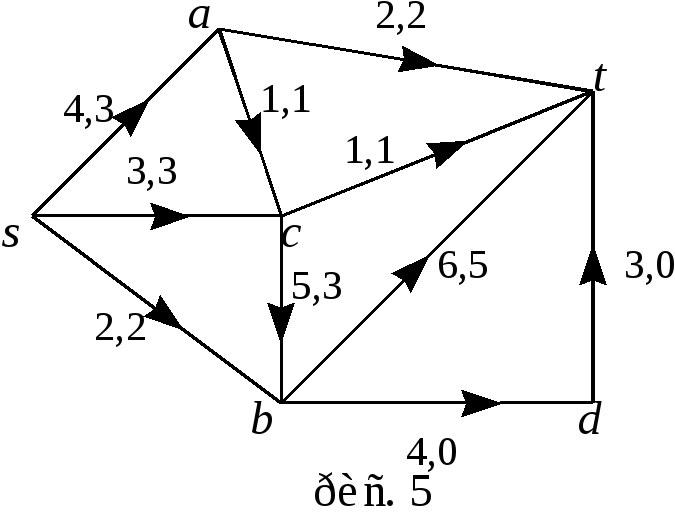аг 4. ,

,

поток указан на рис. 5;

.

Для цепи, изображенной на рисунке 5 , -дополняющих цепей из в нет. Следовательно, поток является максимальным потоком.

Обоснование алгоритма Форда-Фалкерсона

Предварительно введем ряд понятий и докажем ряд утверждений.

Определение. Разрезом в сети называется пара множеств и , удовлетворяющих условиям:

1. , ;

2. ;

3. .

Через обозначим множество всех дуг, начала которых лежат в , а концы – в , а через - множество всех дуг, начала которых лежат в , а концы – в .

Определение. Положим . Число называется пропускной способность разреза .

Также для разреза введем числовые характеристики:

,

.

Пример 4. Для сети и потока в ней из примера 1, рассмотрим разрез , где и . Имеем: , , .

Лемма 1. Для любого потока и любого разреза справедливо равенство .

Доказательство. Согласно условию сохранения потока в вершинах для произвольной вершины имеем: , или . Следовательно,

. (1)

Кроме того

. (2)

Сложив почленно равенства (1) и (2), получим

,

,

,

.

Первое и третье слагаемые последнего равенства взаимно уничтожаются, следовательно,

,

. ■

Следствие 1. .

Доказательство. Пусть , . Тогда , и равенство из леммы 1 запишется следующим образом: . ■

Следствие 2. Для любого потока и любого разреза справедливо неравенство .

Доказательство. Из условия ограничения по пропускной способности , т.е.

.

Тогда с учетом равенства из леммы 1 имеем:

■

Определение. Разрез называется минимальным, если для любого разреза справедливо неравенство

.

Лемма 2. Если для некоторого потока и некоторого разреза выполняется равенство , то поток максимален, а разрез минимален.

Доказательство. Пусть - максимальный поток, а - минимальный разрез. Тогда справедлива следующая цепочка неравенств

.

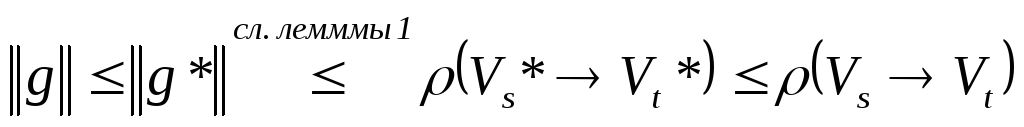Поскольку крайние члены в этой цепочке неравенств совпадают, то она превращается в цепочку равенств, что означает, что поток максимален, а разрез минимален. ■

Лемма 3. Пусть - поток в сети и – -дополняющая цепь из в . Тогда в сети существует поток такой, что

.

Доказательство. Определим в сети функцию по формуле

Докажем, что функция является потоком.

Вначале покажем, что функция неотрицательна и удовлетворяет условию 1) определения потока.

Пусть - прямая дуга цепи . Тогда

.

Пусть - обратная дуга цепи . Тогда

и

.

Таким образом, для любой дуги цепи выполнено . Если , то .

Теперь убедимся в выполнении для функции условия 2) определения потока. Понятно, что это условие следует проверить лишь для вершин , входящих в цепь . Пусть - дуга, по которой «пришли» в вершину , а - дуга, по которой «ушли» из . Каждая из этих дуг может быть как прямой, так и обратной в цепи . Следовательно, возможны четыре различных случая.

1. Пусть обе дуги и прямые. В этом случае,

и ,

так что

и .

Но для потока выполнено условие , следовательно, и для потока имеем .

2. Пусть дуга - прямая и - обратная, т.е. обе дуги входят в вершину . В этом случае,

и ,

так что

и .

Так как для потока выполнено условие , то и для потока имеем .

Аналогично рассматриваются случай 3 (обе дуги и - обратные) и случай 4 (дуга - обратная и - прямая).

Таким образом, мы показали, что функция - поток в цепи .

Определим теперь величину потока . Напомним, что . Из вершины дуги только выходят, поэтому та единственная дуга с началом в вершине , которая входит в цепь , является прямой дугой цепи . Следовательно, для нее выполнено равенство . На остальных дугах, выходящих из , поток не менялся, так что имеем:

. ■

Объединяет приведенные выше результаты следующая теорема.

Теорема (Форд, Флакерсон). Для потока в сети следующие условия эквивалентны:

1. поток максимален;

2. не существует - дополняющей цепи из в ;

3. существует разрез , для которого .

Доказательство. Доказательство проведем по следующей схеме: .

. Будем рассуждать от противного. Предположим, что для максимального потока найдется -дополняющая цепь из в . Тогда по лемме 3 существует поток такой, что , т.е. . Полученное неравенство противоречит тому, что поток максимален.