
Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 3 / параграф 3.15
.doc3.15. Ориентированные графы
Определение. Пусть
![]() -
конечное непустое множество (назовем
его множеством вершин);
-
конечное непустое множество (назовем
его множеством вершин);
![]() - конечное множество (назовем его
множеством дуг);
- конечное множество (назовем его
множеством дуг);
![]() -
отображение множества
-
отображение множества
![]() в
в
![]() (назовем его отображением инцидентности).
Тройку
(назовем его отображением инцидентности).
Тройку
![]() называют ориентированным
графом или, короче, орграфом.
называют ориентированным
графом или, короче, орграфом.
Элементы множества
![]() называют
вершинами, а элементы множества
называют
вершинами, а элементы множества
![]() - дугами.
- дугами.
Пусть вершины
![]() ,
,
![]() и дуга
и дуга
![]() таковы, что
таковы, что
![]() .
В этом случае будем также писать
.
В этом случае будем также писать
![]() .
Вершина
.
Вершина
![]() называют началом дуги
называют началом дуги
![]() ,
а вершина
,
а вершина
![]() - ее концом. При этом говорят, что
дуга
- ее концом. При этом говорят, что
дуга
![]() исходит (выходит) из вершины
исходит (выходит) из вершины
![]() и заходит в вершину
и заходит в вершину
![]() .
Дуга
.
Дуга
![]() и вершина
и вершина
![]() (
(![]() )
называются инцидентными.
)
называются инцидентными.
Число дуг, выходящих из вершины
![]() ,
называется полустепенью исхода
вершины
,
называется полустепенью исхода
вершины
![]() и обозначается
и обозначается
![]() .
Число дуг, заходящих в вершину
.
Число дуг, заходящих в вершину
![]() ,
называется полустепенью захода
вершины
,
называется полустепенью захода
вершины
![]() и обозначается
и обозначается
![]() .
Число
.
Число
![]() называется степенью вершины
называется степенью вершины
![]() .
.
Понятие изолированных и висячих вершин, кратных дуг и петель вводится для орграфов так же, как и для неориентированных графов.
Лемма. Пусть
![]() -
произвольный орграф. Тогда
-
произвольный орграф. Тогда
![]() .
.
Это утверждение аналогично лемме о рукопожатиях, рассмотренной нами в параграфе 3.1. для неориентированных графов; его часто называют орлеммой о рукопожатиях.
Определение. На множестве орграфов
введем бинарное отношение, называемое
отношением
изоморфизма, которое определим
следующим образом: будем говорить, что
орграфы
![]() и
и
![]() связаны отношением изоморфизма,, если
существует пара взаимно однозначных
отображений
связаны отношением изоморфизма,, если
существует пара взаимно однозначных
отображений
![]() и
и
![]() таких, что для любой дуги
таких, что для любой дуги
![]() выполнено условие:
выполнено условие:
![]() .
.
Орграфы
![]() и
и
![]() ,
связанные отношением изоморфизма,
называют изоморфными и пишут
,
связанные отношением изоморфизма,
называют изоморфными и пишут
![]() .
.
По аналогии с понятием геометрического неориентированного графа вводится понятие геометрического орграфа, а также понятие геометрической реализации (диаграммы) орграфа. Разница состоит лишь в том, что отрезкам непрерывных кривых, изображающим дуги, придают направление.
С каждым орграфом
![]() естественно связать неориентированный
граф
естественно связать неориентированный
граф
![]() ,
называемый основанием данного
графа. Для получения основания необходимо
каждую дугу
,
называемый основанием данного
графа. Для получения основания необходимо
каждую дугу
![]() графа
графа
![]() заменить на такое ребро
заменить на такое ребро
![]() ,
что если
,
что если
![]() ,
то
,
то
![]() .
.
Пример 1. На
рисунках изображен ориентированный
граф
![]() и его основание
и его основание
![]() .
.
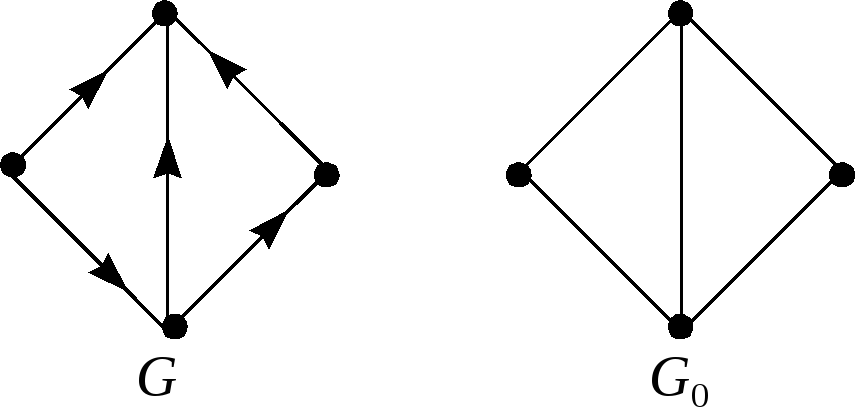
Орграф, основание которого есть полный граф, называется турниром.
Определение. Орграф называется связным, если связно его основание.
Определение. Путем
длины
![]() на орграфе
на орграфе
![]() называется последовательность
вершин и дуг
называется последовательность
вершин и дуг
![]()
такая, что для любой дуги
![]() вершина
вершина
![]() является началом, а вершина
является началом, а вершина
![]() -
концом.
-
концом.
Про такой путь говорят, что он соединяет
вершины
![]() с
с
![]() ,
кратко называют
,
кратко называют
![]() -
путем; вершины
-
путем; вершины
![]() и
и
![]() называют при этом соответственно началом
и концом пути.
называют при этом соответственно началом
и концом пути.
Случай, когда длина пути равна нулю, не исключается; в этом случае путь сводится к одной вершине.
Определение. Замкнутый путь без повторяющихся вершин (за исключением концевых) называется контуром.
Контур нулевой длины не рассматривают.
На множестве вершин орграфа
![]() введем бинарное отношение – отношение
достижимости, полагая:
введем бинарное отношение – отношение
достижимости, полагая:
![]() .
.
Несложно показать, что отношение достижимости является отношением эквивалентности
Определение. Орграф называется сильно связным или орсвязным, если любые его две вершины связаны отношением достижимости.
Очевидно, что сильно связный граф является связным; обратное утверждение в общем случае неверно.
Пример 2.
Граф
![]() из примера 1 связным является, а орсвязным
– нет.
из примера 1 связным является, а орсвязным
– нет.
Пусть
![]() - произвольный неориентированный граф.
Превратим каждое его ребро в дугу, придав
ребру одно из направлений. Полученный
при этом орграф будем называть ориентацией
графа
- произвольный неориентированный граф.
Превратим каждое его ребро в дугу, придав
ребру одно из направлений. Полученный
при этом орграф будем называть ориентацией
графа
![]() .
.
Если среди ориентаций графа
![]() найдется сильно связный граф, то граф
найдется сильно связный граф, то граф
![]() называется
ориентируемым.
называется
ориентируемым.
Пусть
![]() - произвольный орграф с m
вершинами и n дугами.
Пометим его дважды, т.е. упорядочим
множества его вершин и дуг.
- произвольный орграф с m
вершинами и n дугами.
Пометим его дважды, т.е. упорядочим
множества его вершин и дуг.
Определение. Матрицей
смежности орграфа
![]() называется матрица
называется матрица
![]() размера
размера
![]() ,
элементы которой
,
элементы которой
![]() ,
где
,
где
![]() - число дуг, исходящих из вершины
с номером
- число дуг, исходящих из вершины
с номером
![]() и заходящих в вершину с номером
и заходящих в вершину с номером
![]() .
.
Определение. Матрицей
инцидентности орграфа
![]() называется матрица
называется матрица
![]() размера
размера
![]() ,
элементы которой
,
элементы которой
![]() определены следующим:
определены следующим:
1.
![]() ,
если вершина с номером i
– начало дуги с номером j
и j-ая дуга – не
петля;
,
если вершина с номером i
– начало дуги с номером j
и j-ая дуга – не
петля;
2.
![]() ,
если вершина с номером i
– конец дуги с номером j
и j-ая дуга – не
петля;
,
если вершина с номером i
– конец дуги с номером j
и j-ая дуга – не
петля;
3.
![]() во всех остальных случаях.
во всех остальных случаях.
Пример 3.

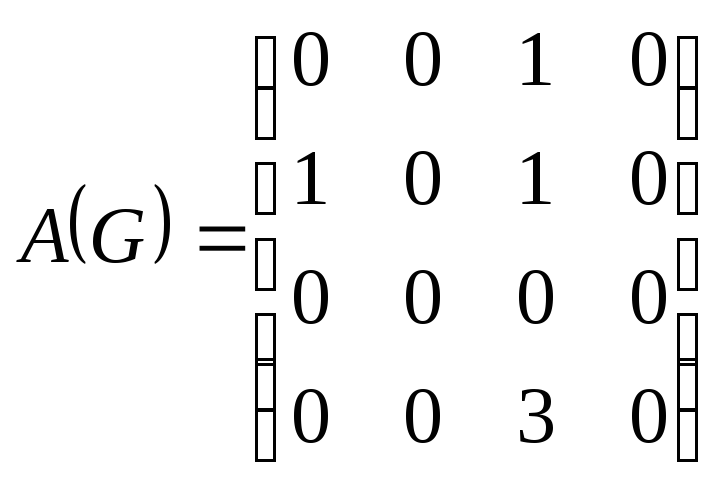 ;
;
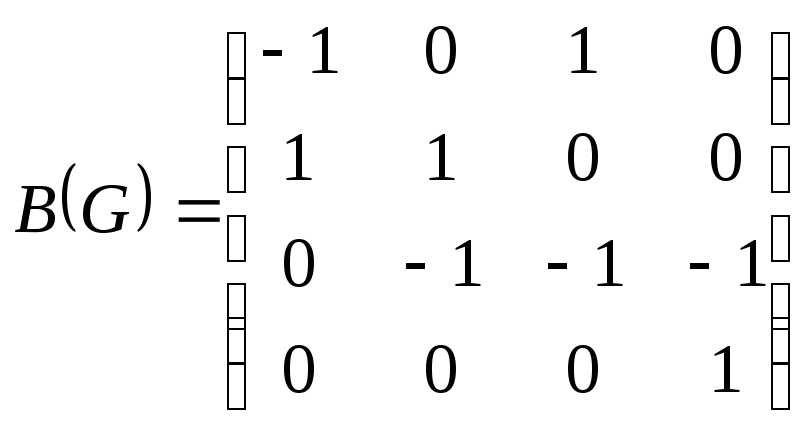 .
.
