Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 3 / параграф 3.16

3.16. Задача о кратчайшем пути

Определение. Взвешенный связный орграф называется сетью.

Пусть на графе имеется путь из вершины в вершину и - последовательность дуг этого пути. Число называется весом или длиной пути .

Наименьшую из длин -путей назовем расстоянием от до , а тот -путь, длина которого равна расстоянию от до , будем называть кратчайшим -путем.

Задача о кратчайшем пути состоит в следующем: в заданной сети найти расстояние и кратчайший путь от фиксированной вершины до остальных вершин.

Рассмотрим алгоритм Дейкстры, позволяющий решить задачу о кратчайшем пути.

Для удобства изложения введем ряд условных обозначений. Если существует хотя бы один путь из вершины в вершину , то расстояние от до будем обозначать через . Каждой паре вершин и будем ставить в соответствие число , полагая его равным весу дуги, исходящей из и заходящей в , если таковая существует. Если же такой дуги в графе нет, то полагаем .

Будем говорить, что вершина ближайшая к вершине из подмножества множества вершин графа, если расстояние от до является наименьшим из расстояний от вершины до других вершин из множества .

В основе алгоритма Дейкстры лежит принцип жадности, заключающийся в последовательном вычислении расстояний сначала до ближайшей к вершине, затем до следующей ближайшей и т.д.

Алгоритм Дейкстры. 0-ой шаг. Находится первая ближайшая к вершине вершина: такой вершиной является сама вершина , для которой .

-ый шаг. Пусть к началу шага определены вершин, ближайшие к вершине , т.е. определено множество , и для всех этих вершин вычислены расстояния , . Обозначим через множество .

Если множество пусто, то все возможные расстояния от фиксированной вершины до остальных вершин определены на -ом шаге.

В противном случае из равенства для каждой вершины положим

.

Если ни для одной вершины этот минимум определить нельзя, то все возможные расстояния от фиксированной вершины до остальных вершин определены на -ом шаге.

В противном случае из равенства

,

определится вершина , ближайшая к вершине из вершин подмножества , причем

.

Таким образом, по окончании -го шага множество вершин, до которых от вершины вычислено расстояние, расширяется на один элемент.

Обоснование алгоритма Дейкстры. Обоснуем вначале равенство . Пусть - произвольный -путь. Поскольку - длина одного из путей из вершины в вершину , то достаточно доказать неравенство . Среди всех вершин пути выберем вершину с наименьшим номером среди тех, которые не входят в множество . Так как начальная вершина пути входит в , а конечная не входит в , то такой номер найдется. Итак, , . Тогда из определения и длины пути вытекают соотношения

.

Кроме того, в силу выбора вершины имеем, что . С учетом этих неравенств получаем, что . Следовательно, .

Осталось убедиться, что вершина является -ой ближайшей к вершиной. Для этого достаточно доказать неравенство для всех . Зафиксируем одну из вершин . Обозначим через кратчайший путь из вершины в вершину , а через - кратчайший путь из вершины в вершину . Тогда и . Выше доказано равенство . Повторим для пути рассуждения, приведенные в первой части обоснования для пути . Среди всех вершин пути выберем вершину с наименьшим номером среди тех, которые не входят в множество . Имеем: , . Тогда

.

Кроме того, в силу выбора вершины имеем, что . Следовательно,

,

что и требовалось доказать. ■

Восстановление кратчайшего пути. Кратчайший путь от вершины до вершины восстанавливается пошагово, начиная с вершины до возврата к вершине . Опишем один шаг возвращения. Для вершины среди всех вершин , для которых существует дуга, ведущая из в , находится такая дуга, для которой выполнено условие . Тем самым восстанавливается последняя дуга кратчайшего пути от до .

П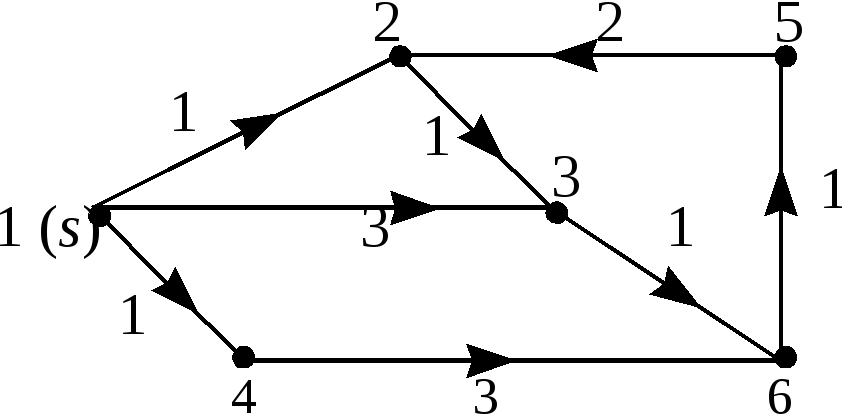ример 1. В графе, изображенном на рисунке, найти расстояние от вершины до остальных вершин и восстановить кратчайший путь от вершины 1 до вершины 5.

k
0		0
1	{1}		1	3	1
2	{1,2}			2	1
3	{1,2,4}			2			4
4	{1,2,4,3}						3
5	{1,2,4,3,6}					4

Кратчайший путь от первой вершины до пятой вершины проходит последовательно через вершины 1,2,3,6,5.

58