Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 3 / параграф 3

3.1. Начальные понятия теории графов

Определение. Пусть и - конечные множества, ; - отображение множества в множество одно и двухэлементных подмножеств множества . Тройку называют неориентированным графом (или просто графом).

Элементы множества и называют соответственно вершинами и ребрами. Множество вершин и ребер графа будем также обозначать и . Отображение называют отображением инцидентности.

П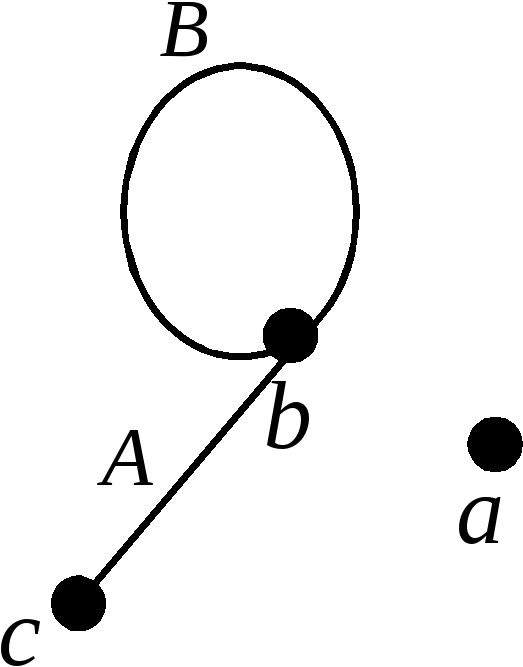ример 1. : , , , .

Граф удобно представлять в виде диаграмм, на которых вершинам соответствуют помеченные точки плоскости, а ребрам – помеченные непрерывные кривые, соединяющие эти точки. Так, граф из примера 1 можно представить диаграммой, изображенной на рисунке.

Если , где , то говорят, что ребро соединяет вершины и . В этом случае будем писать . Если , то ребро называют петлей в вершине . В этом случае будем также писать и говорить, что соединяет вершину саму с собой.

Если - некоторое ребро данного графа, то вершины , называются смежными; говорят также, что , –концевые вершины ребра .

Ребра и называются смежными, если они имеют общую концевую вершину.

Если - концевая вершина ребра , то ребро и вершина называются инцидентными.

Если и , то ребра и называются кратными. Число ребер, инцидентных вершине , (петля учитывается дважды) называется степенью вершины и обозначается .

Если , то вершина называется изолированной.

Если , то вершина называется висячей. Ребро, инцидентное висячей вершине, называется висячим.

Пример 2. Пусть , а . Отображение инцидентности задано следующим образом: , , , , , .

Для наглядности представим граф диаграммой.

Вершины , - концы ребра . Ребра , - кратные. Вершины и - смежные. Вершина инцидентна ребрам , , . , , , , . Вершина - висячая, ребро - висячее, вершина - изолированная.

Лемма (о рукопожатиях). Для любого графа сумма степеней вершин равна удвоенному числу ребер, т.е.

.

Доказательство. При подсчете суммы степеней вершин произвольное ребро внесет вклад, равный 1, как в степень вершины , так и в степень вершины , т.е. будет учтено в сумме дважды. ■

Следствие. В любом графе число вершин нечетной степени либо четно, либо равно 0.

Доказательство. Пусть и - соответственно множества вершин четной и нечетной степени. Тогда

.

Ясно, что первое слагаемое четно. Поэтому второе слагаемое либо также четно, либо равно нулю. В первом случае, так как во второй сумме все слагаемые нечетны, то их число четно. Следовательно, множество либо содержит четное число вершин, либо пусто. ■

Граф без петель и кратных ребер называется обыкновенным графом.

Будем называть граф одноэлементным, если он имеет единственную вершину. Граф называется нулевым, если множество его ребер пусто. Нулевой граф с вершинами будем обозначать

Обыкновенный граф называется полным графом, если любые его две различные вершины смежные. Для полного графа с вершинами применяется обозначение .

Пример 3.

Заметим, что степень каждой вершины полного графа равна , так что

.

Следовательно, число ребер полного графа с вершинами равно .

Двудольным графом называется обыкновенный граф, множество вершин которого может быть разбито на два непустых непересекающихся подмножества (доли), так что концы каждого ребра графа принадлежат разным долям.

Двудольный граф называется полным двудольным графом, если любые две его вершины, принадлежащие разным долям, смежные.

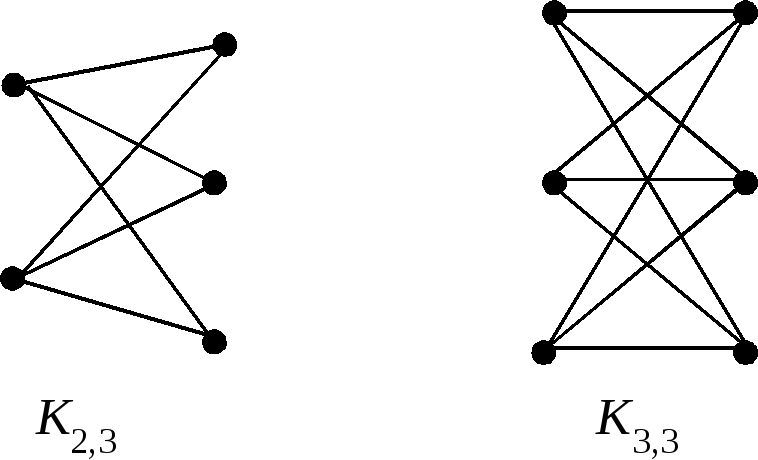
Полный двудольный граф с вершинами в одной доле и вершинами в другой () обозначают .

Пример 3.

Граф, вершины которого - помеченные точки плоскости или пространства, а ребра – непрерывные кривые, соединяющие данные точки (причем не проходящие через другие вершины), называется геометрическим.

35