Литература / Олейник.Лекции по дискретной математике / вариант .doc / Глава 3 / Параграф 3

3.2. Изоморфизм графов

Определение. На множестве неориентированных графов введем бинарное отношение, называемое отношением изоморфизма, которое определим следующим образом: будем говорить, что графы и связаны отношением изоморфизма,, если существует пара взаимно однозначных отображений и таких, что для любого ребра выполнено условие:

.

Графы и , связанные отношением изоморфизма, называют изоморфными и пишут .

П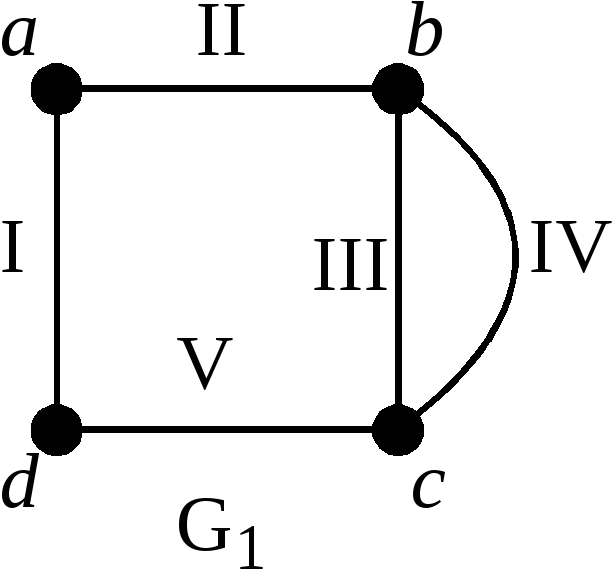ример 1. На рисунке изображены три геометрических графа.

П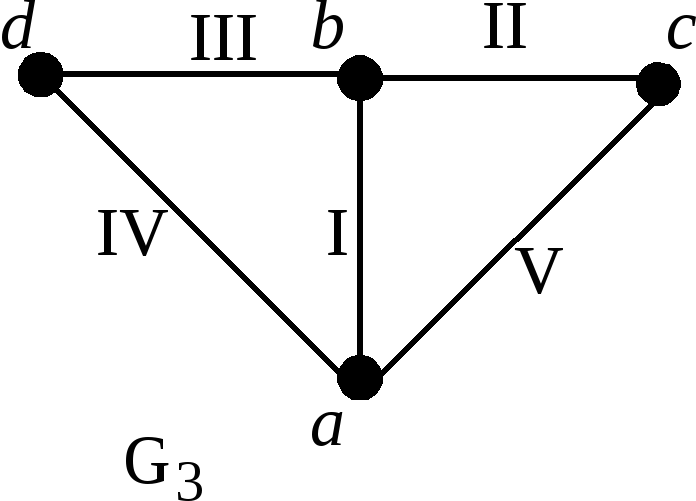окажем, что графы и неизоморфны. Будем рассуждать от противного. Предположим, что эти графы изоморфны. Тогда существует пара задающих изоморфизм отображений , так что

и .

То есть при изоморфизме образами кратных ребер графа должны быть кратные ребра. Но кратных ребер в графе нет. Следовательно, наше предположение об изоморфизме графов и неверно.

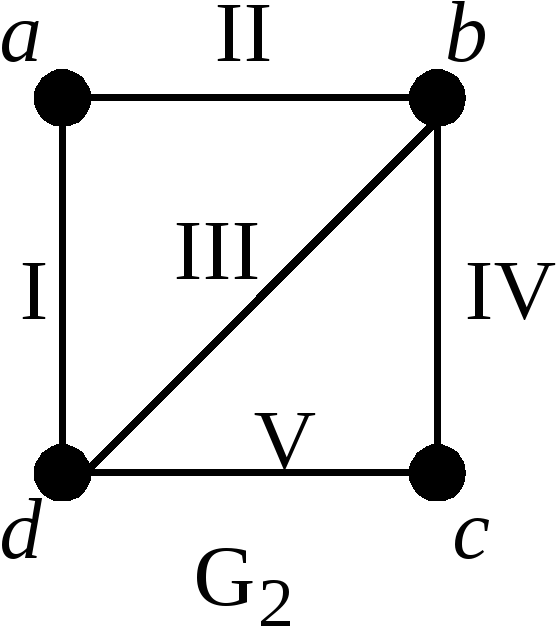
Покажем, что графы и изоморфны. Определим отображения следующим образом: , , , , , , , , . Надо показать, что для каждого ребра графа , если то

Вначале проверим выполнение этого условия для ребра графа , т.е. покажем, что высказывание истинно.

Действительно, с учетом того, что , , , вместо можем записать , что верно (см. рис.).

Аналогичную проверку делаем и для остальных ребер графа .

Утверждение 1. Изоморфизм – отношение эквивалентности на множестве неориентированных графов, т.е. оно рефлексивно, симметрично и транзитивно.

Доказательство. 1. Рефлексивность имеет место, поскольку тождественное преобразование взаимно однозначно.

2. Симметричность имеет место, поскольку взаимно однозначные отображения обратимы и обратные к ним взаимно однозначны.

3. Транзитивность имеет место, поскольку композиция взаимно однозначных отображений есть взаимно однозначное отображение. ■

Замечание. В дальнейшем, если не оговорено противное, графы рассматриваются с точностью до изоморфизма, то есть объектом изучения являются не отдельные графы, а классы эквивалентности по отношению изоморфизма.

Упражнение. Доказать, что если графы и изоморфны и - пара взаимно однозначных отображений, реализующих этот изоморфизм, то для любой вершины графа выполнено: .

Утверждение 2. Для любого графа существует изоморфный ему геометрический граф (и в , и в ) (его называют геометрической реализацией).

Доказательство. Вершинам графа поставим в соответствие помеченные точки плоскости или пространства; а ребрам - помеченные непрерывные кривые. Точки и кривые пометим именами соответствующих вершин и ребер графа. При этом кривые изобразим так, чтобы их концы совпадали с точками, изображающими вершины, инцидентные соответствующим ребрам графа. ■

Очевидно, что диаграмма – это геометрическая реализация графа.

Определение. Геометрический граф называется правильно реализованным, если его ребра не имеют общих точек, отличных от вершин.

Пример 2. Рассмотрим граф : , , , , , , , .

Н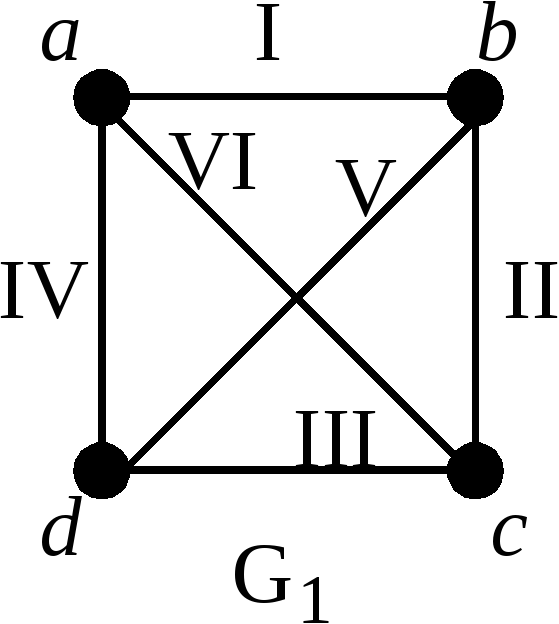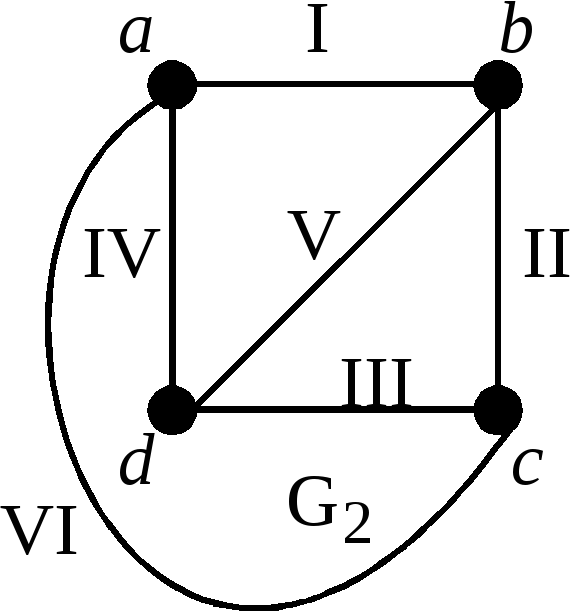а рисунке изображены две геометрические реализации данного графа: и . Граф является правильной геометрической реализацией графа , а граф - нет.

Утверждение 3. Для любого графа существует его правильная геометрическая реализация в .

Доказательство. Опишем алгоритм построения правильной реализации любого графа .

В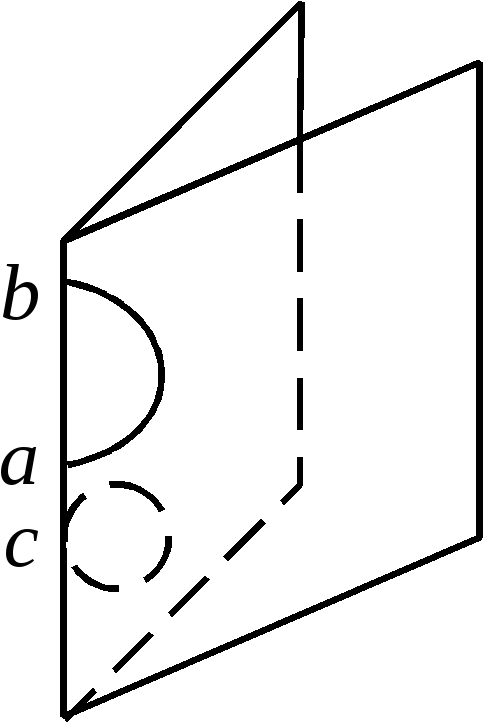озьмем в произвольную прямую . На прямой отметим столько точек, сколько вершин графа. Точки пометим теми же буквами, что и вершины графа.

Через прямую проведем столько различных плоскостей, сколько ребер графа (каждому ребру будет соответствовать своя плоскость). Если ребро с концами и не является петлей, то в соответствующей ему плоскости на отрезке как на диаметре построим полуокружность, которую пометим так же как и ребро: . Если ребро - петля и - инцидентная ему вершина, то в соответствующей данному ребру плоскости изобразим единичную окружность, касательную к в точке , и пометим ее .

Очевидно, построенный таким образом геометрический граф есть правильная геометрическая реализация графа . ■

Заметим, что не всякий граф имеет правильную геометрическую реализацию в .

Определение. Если существует правильная геометрическая реализация графа на плоскости, то граф называется планарным.

37