5.10. Краткие сведения о переходных процессах в цепях с распределенными параметрами
Исходные уравнения и их решение.
Из
уравнений (5.1) и (5.4) при
и
следует, что ток и напряжение являются
функциями двух переменных: расстояния
х
от начала линии и времени t.
После их дифференцирования по х
и по t
можно
получить следующее уравнение:
,
где
или
есть
скорость распространения электромагнитной
волны по линии. Если дифференцирование
провести в обратном порядке, то можно
получить уравнение для тока:
.
Видно, что полученные уравнения являются
уравнениями второго порядка в частных
производных. Из курса математики
известно, что уравнения такого вида
называют волновыми.
Решением
этих уравнений является сумма любых
функции f1
и f2
и причем
аргументом функции f1
является
,
аргументом функции f2
-
:
Для сокращения записи в дальнейшем будем обозначать:
Следовательно,
,
где индексы «о» и «п» относятся к
отраженной и падающей (волнам).
Вид функций f1 и f2 определяется граничными условиями в начале и конце линии. Функции f1 и f2 в общем случае должны позволять дважды дифференцировать их по x и t.
Решение
уравнения для тока:
Для сокращения записи обозначим:
Тогда:
5.11. Практическое приложение к разделу
5.1*. Найти фазовую скорость для воздушной двухпроводной линии с малыми потерями.
Решение. Из условий
малых потерь следует, что =
.Поэтому
ф=
/=
.
Индуктивность единицы длины двухпроводной воздушной линии
L0=(0/)ln(d/r),
где 0— магнитная постоянная;d—расстояние между осями проводов;r—радиус каждого провода.
Емкость единицы длины воздушной двухпроводной линии
C0=0/ln(d/r), где0— электрическая постоянная.
Фазовая скорость
ф=
5.2*. Найти длину электромагнитной волны при f=50 и 50 106Гц.
Решение. При f=50Гц
=
=6000
км.
При f=50 106Гц=6 м
5.3*. Дано:
=0,963 Нп; Zс=700 Oм. НайтиZ1иZ3.
Решение. Z1/Z3 =ch0,963* - 1 = 0,5;Z1=0,5Z3;ZC=2,25Z1;
Z1=311 Ом;Z3=622 Ом.
5.4*. Телеграфный кабель имеет параметры:
r0=7 Ом/км,L0=0.3*10-3Гн/км,C=0.2 мкф/км,g0=0.5*10-6См/км.
Определить волновое сопротивление кабеля, коэффициент затухания и фазы, скорость распространения волны и длину волны на частоте f=800 Гц.
Определить ток и напряжение в начале линии, если длина кабеля l=20 км, на конце включена активная нагрузкаZ2=r2=100 Ом, а напряжение на нагрузкеU2=4.5 В.
Решение:
Волновое сопротивление кабеля определяется по формуле:
В
данной задаче
=2
,
поэтому
=
=
=
=
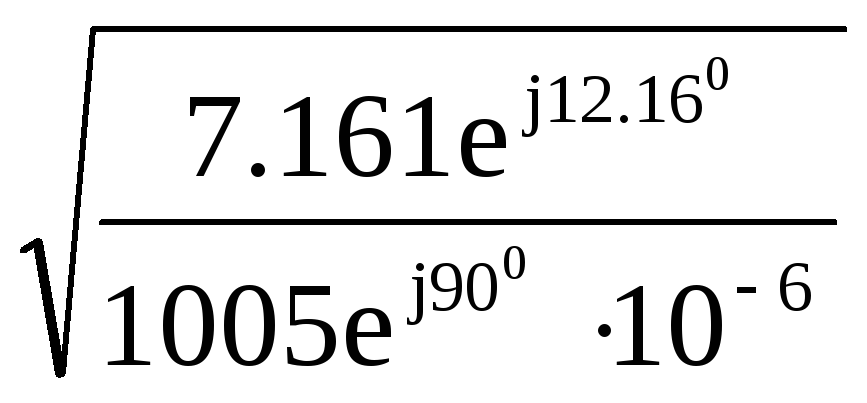=84,41e-j38.92
Ом=65.67-j53.03 Ом.
Коэффициент распространения:
=
=0,08483ej51.08
=
=0.05329+j0.066;
Отсюда
коэффициент затухания:
=0.05329
Нп/км.
Коэффициент
фазы:
=0.066
рад/км=3.7810 /км.
Напряжение и ток в начале линии можно определить по формулам:
;
;
Подстановка
численных значений дает: (при этом
А.)
=
=3.914e-j17.75
ej75.62
e1.066+1.421ej57.08
e-j75.62
e-1.066=11.36ej57.87
+0.4894e-j18.54
=
=6.506+j9.465=11.5ej55.5
,B.
=-0.02135+j0.1316=
=0.1333ej99.21
,A.
Таким образом, действующее значение тока и напряжению на входе линии:
U1=11.5B;I1=0.1333A.
Активная мощность на входе:
P1=Re[
]=Re[11.5ej55.5
0.1333e-j99.21
]=1.108
Вт.
На выходе:
P2=
Rн=0.0452*100=0.2025
Вт.
К.П.Д. линии:
=0.1828
(18.28%)
Скорость распространения волны (фазовая скорость) равна
км/с.
Длина волны:
=2
/0.066=95.2
км.
5.5. Воздушная
трехфазная линия электропередачи длиной
=900
км, имеет параметры:
R0=
Ом/км,G0=
См/км,L0=
Гн/км,C0=
Ф/км.
Напряжение в конце линии: U2Ф=220 кВ,
Мощность нагрузки: P2=300 МВт,
Коэффициент
мощности нагрузки:
=1
Частота напряжения: f=50 Гц.
Найти фазное напряжение, ток и активную мощность в начале линии.
Примечание: Нагрузка симметричная, поэтому расчет можно провести для одной фазы.
5.6. Двухпроводная линия связи имеет параметры:
R0=
Ом/км,G0=
См/км,L0=
мГн/км,C0=
Ф/км.
и работает в режиме согласованной нагрузки.
Определить длину линии, если затухание сигнала на частоте f=800 Гц составляет 1.3 Нп.
5.7. Через каждый километр длины линии (задача 5.5)включили добавочную катушку индуктивности, так что линия стала неискажающая.
Какое сопротивление нужно включить в конце линии, чтобы был обеспечен режим согласованной нагрузки? Какую длину может иметь линия, если допустимое затухание сигнала составляет 1.3 Нп? (Средняя частота сигнала f=800 Гц.)
5.8. Для двухпроводной
линии длиной
,
частотой тока и напряженияfв общем виде получить выражения,
позволяющие определить волновое
сопротивлениеZ, коэффициент
распространения
,
коэффициент затухания и фазы
и
,
а также параметры линии:R0,L0,G0,C0если известно
сопротивление холостого хода и короткого
замыканияZ1x=Z1xe
,Z1k=Z1ke
.
Что изменится, если ввести условие, что данная линия является неискажающая?
5.9. Неискажающая
линия длиной
=100
км питается синусоидальным напряжениемU=100B, частотойf=104 Гц. Волновое
сопротивление линииZ=300
Ом, коэффициент распространения
=
.
Найти напряжение и ток в конце линии при активной нагрузке:
а) Rн=300 Ом.
б) Rн=600 Ом
5.10. Коаксиальный
кабель с волновым сопротивлением Z=75
Ом имеет длину
100м.
Напряжение на входе U1=200 мВ. Частотаf=50 МГц.
Определить напряжение на выходе для трех случаев:
а) кабель разомкнут на конце;
б) сопротивление нагрузки Zн=Z;
в) сопротивление нагрузки Zн=Z/2:
Кабель можно рассматривать как линию без потерь. Фазовую скорость принять равной половине скорости света.
5.11. Определить параметры воздушной линии без потерь, если волновое сопротивление линии Z=400 Ом.
5.12. В конце воздушной линии без потерь с волновым сопротивлением Z=150 В и нагрузкойZн=300 Ом, токI2=10 мА, частота токаf=100 мГц.
Выяснить, на каких расстояниях от конца линии будут находиться максимум и минимум напряжения в этих точках?
5.13. На рис. 5.9.
показана конструкция простейшей
телевизионной антенны. Длина антенны
берется равной половине длины волны
телевизионного сигнала (
).
Определить, какую длину должна иметь
антенна при частотах:
f=50 Мгц, 100 Мгц, 150 Мгц, 200 Мгц ?
5.14. Линия без потерь с параметрами:
L0=
Гн/км,C0=
Ф/км
имеет
длину
км. Напряжение на входеU1=20
В, частотаf=5 кГц.
Определить ток в начале и конце линии, а также напряжение на выходе для трех случаев:
а) линия разомкнута;
б) замкнута накоротко;
в) нагружена на волновое сопротивление.
5.14.* Воздушная линия с волновым сопротивлением Z=400 Ом (которая может рассматриваться как линия без потерь) подключена к источнику постоянного напряженияU0=10 кВ. Определить амплитуды напряжения и тока в линии:
а) при подключении в конце линии активной нагрузки Rн=800 Ом.
б) при отключении активной нагрузки в конце линии.
Решение: а) при подключении активной нагрузки в линии возникает обратная волна напряжения с прямоугольным фронтом. Напряжение и ток этой волны рассчитывается по формулам:
В.
А.
При
движении обратной волны от конца линии
к ее началу, напряжение в линии снижается
и становится равным: 
В.
б)
при отключении нагрузки в линии также
возникает обратная волна, напряжение
и ток которой определяются по формулам:
;
;
где Iн – ток нагрузки (в нашем случае Iн=8.33 А)
В результате наложения обратной волны и напряжения источника напряжение в линии повышается до значения
В.
После окончания переходного процесса (волны движутся со скоростью света) напряжение в начале линии становится равным U0.
5.15. Определить напряжение в конце воздушной линии с волновым сопротивлением Z=400 Ом, если по линии движется волна напряжения с прямоугольным фронтомU0=10 кВ для случаев:
а) линия разомкнута на конце ;
б) линия замкнута на активное сопротивление Rн=Z;
в) линия замкнута на активное сопротивление Rн=2Z.
5.16. Волна прямоугольной формы U0=6 кВ переходит из кабельной линии с волновым сопротивлениемZ1=80 Ом в воздушную с волновым сопротивлениемZ2=600 Ом. Найти напряжение и ток отраженной и преломленной волн. Что изменится, если волна будет переходить из воздушной линии в кабельную?
5.17. Чему будет
равно напряжение в конце воздушной
разомкнутой линии длиной
=600
км спустяt=1 мс; 2 мс; 4 мс;
6 мс; после подключения линии к источнику
сU=220 кВ?
5.18. Две последовательно
соединенные линии (
км,Z1=50 Ом,
км,Z2=450 Ом) на холостом
ходу подключаются к источнику постоянного
напряженияU=10 кВ. Найти
напряжение и ток в линиях спустяt=100c; 120c; 140c;
после подключения.
Примечание: первая линия является кабельной, и фазовая скорость для нее приблизительно в 2 раза меньше скорости света.
5.19*. Для некоторой линии длиной 5 км на частоте 1000 Гц были проведены опыты по определению ее входного сопротивления при холостом ходе и коротком замыкании на конце линии. Оказалось, что Zвx x.x=535e-j64 0м иZвх к.з=467,5e-j10 Ом. Требуется найти волновое сопротивлениеZви постоянную распространенияэтой линии.
Решение. При
холостом ходе, когда Z2=
,
Zвх х.х=Zв/th l.
При коротком замыкании, когда Z2=0,
Zвх к.з= Zвth l,
отсюда
=
500e-j370Ом;
th
l=
= 0,935еj27.
Постоянную распространения найдем из соотношений:
5.20. Определить R0, L0, G0иС0для линии примера 5.19, полагаяZв =500e-j37Ом и= 0,2еj45 км-1.
Решение. Произведение волнового сопротивления на коэффициент распространения равно: Zв=R0+jL0. Следовательно,
R0+jL0=0,2еj45500e-j37=100ej8=99+j13,9,
или
R0= 99 Ом/км иL0= 13,9/(2• 1000) = 0,00222 Г/км;
/Zв=G0+jC0.
Таким образом,
G0+jC0= 0,2ej45/(500е-j37)= 0,0557 • 103+j0,396 • 10-3.
5.21*. Линия примера 5.20 подключена к постоянному напряжению (=0). Определить напряжение и ток в начале линии, если на конце линии включена нагрузка 400 Ом и ток в нагрузке 0,5A.
Решение. Волновое сопротивление линии Zвдля постоянного тока:
Постоянная распространения:
=0,0743
км-1.
Тогда напряжение и ток при y=l равны:
;
.
По условию, I2 = 0,5 A; U2= I2R2 = 0,5 • 400 = 200 В; l = l=0,0743•5=0,371; chl=ch0,371=1,07, shl=sh0,371=0,379. Следовательно,
U1 = 200 • 1,07 + 0,5 • 1330 • 0,379 = 466 В;
I1 = 0,5 • 1,07 + (200/1330) • 0,379 = 0,694 А.
5.22*. Линия примера
5.19 короткозамкнута на конце и присоединена
к источнику синусоидального напряжения
частотой 1000 Гц. Определить напряжение
и ток в начале линии, если ток в конце
линии
=1
А.
Решение. При коротком замыкании
=
Zв
sh l;
и
=
ch
l.
По данным примера 5.19,
=+j=0,1414+j0,1414 км-1; l=5 км;
l= 0,707 +j0,707;Zв=500е-j37 Ом.
el =е0,707 ej0,707 =2,02 (cos 40°20' + jsin 40°20') = 1,54 + j1,305;
e-l = е-0,707 e-j0,707 =0,495 (cos 40°20' - jsin 40°20') = 0,377 + j0,32;
ch l = 0,5(еl + e-l)= 0,96 + j0,4925 = 1,07еj27';
sh l = 0,5 (еl - е-l) = 0,582 + j0,812= еj54.
Следовательно,
=
Zв
sh l=500e-j37ej54=500ej17
В;
=
ch
l=1,07ej27
A.
5.23*. Линия примера
5.19 замкнута на активное сопротивление
Z2=400 Ом.
Определить
и
если по нагрузке протекает ток
=0,5
А;f=1000 Гц.
Решение.
=
Zв
сh l+
Zвsh
l=
В;
=
(
/Zв)
sh l
+
ch
l=0,8
A.
5.24*. По данным
примера 5.23 определить комплекс
действующего значения падающей волны
в начале линии (
).
Решение. Постоянная интегрирования:
=A2ejп=0,5(
+
Zв)=
В.
5.25. Записать выражение для мгновенного значения падающей волны напряжения в начале и конце линии по данным примера 5.24.
Решение. Мгновенное значение падающей волны напряжения
в
начале линии при x=0
431
sin(t-19°30').
Мгновенное
значение падающей волны напряжения в
конце линии при х=lв общем виде
A2e-l
sin(t+п-l);отсюда
e-l =е-0,707 =0,495; l=0,707 рад = 40°20';
А2e-l=
4310,495
=301 В;
п-l = 19°30' - 40°20' = 20°50'.
Следовательно, мгновенное значение падающей волны напряжения в конце линии 301 sin (t— 20°50') В.
5.26*. Определить затухание в неперах для линии примера 5.19, если на конце ее включена согласованная нагрузка.
Решение. Затухание в неперах равно l. Так как произведениеl=0,14145 =0,707, то затухание линии равно 0,707 Нп.
5.27*. Какую дополнительную индуктивность L0 допнужно включить на каждом километре телефонной линии с параметрами:R0 = 3 Ом/км; L0 = 2 10-3 Г/км; С0 =10-6 Ом-1 км-1; С0 = 6 10-9 Ф/км, чтобы линия стала неискажающей?
Решение. Для того чтобы линия была неискажающей, ее параметры должны удовлетворять уравнению:
L0 доп + L0 =R0C0/G0=3610-9/10-6=1810-3 Г/км. L0 =18-2=16 мГ/км.
5.28*. Определить наименьшую длину короткозамкнутой на конце двухпроводной воздушной линии, чтобы при частоте 108Гц входное сопротивление ее равнялось800jОм. Расстояние между осями проводовd=20 см, радиус каждого проводаr=2 мм.
Решение. Входное сопротивление равно:
.
Для двухпроводной линии
;
=377
Ом;
=377
ln(200/2)/=553
Ом.
По условию, 800j =j553 tg y.
Отсюда
tg y = 800/553 = 1,445; y = 55°20' = 0,963 рад;
=1/(31010)с/см;
=
=
=2108
/(31010)=2,092
• 10-2 см-1.
Искомая длина линии
y=0,963/(2,09210-2)=46,1см.
5.29*. В симметричной Т-схеме Z1=100Ом,Z3 =-500jОм. Определить характеристическое сопротивление четырехполюсника и произведениеlэквивалентной ему линии с распределенными параметрами.
Решение. Определим коэффициенты А и В :
A=D=1+Z1/Z3=1+100/(-500j)=1+0,2j=1,02
B=2Z1+
Z12/Z3=200+104/(-500j)=200+20j
200
C=1/Z3=1/(-500j)=0,002
.
Волновое сопротивление:
=
Ом
Тангенс гиперболический:
=
=0,498 + j0,369.
Вычислим l:
=
l
= 0,5 In 2,475 = 0,454; l=
25°5'
0,437рад;
l= 0,454+j0,437.