
442
.pdf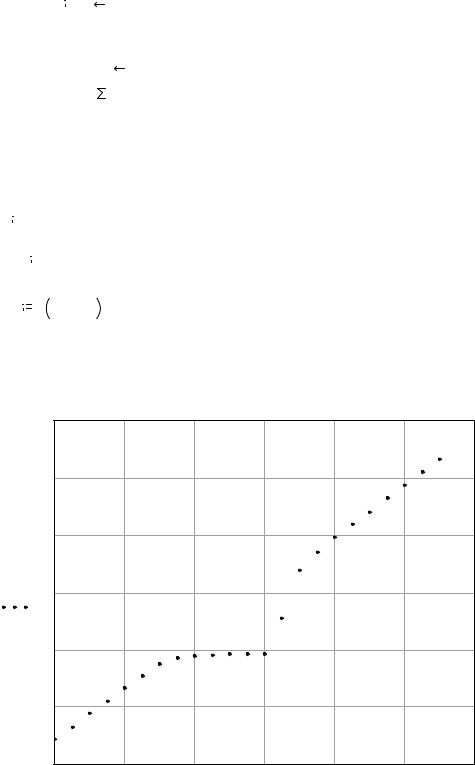
71
Функция, возвращающая среднюю угловую скорость, соответствующую моменту Mo
ω ( Mo , N) |
|
|
v |
xr( 0.02, N, y, Mo , D) |
||||||
|
||||||||||
|
|
|||||||||
|
|
|
|
for |
i |
N |
.. N |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
vvi v4,i |
||||||
|
|
|
|
2. |
vv |
|
||||
|
|
|
|
N |
||||||
Нахождение зависимости угловой скорости в функции момента Ω=Ω(Mo)
j  0.. 22
0.. 22
Moj  10
10  0.5.j
0.5.j
Ω j ω Moj , 400
Построение графика зависимостиугловой скорости в функции момента Ω=Ω(Mo)
|
50 |
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
Ω j |
35 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
20 |
12 |
14 |
16 |
18 |
20 |
22 |
|
10 |
||||||
|
|
|
|
Moj |
|
|
|
Рис. 11.6 |
Зависимость угловой скорости вала в функции составляющей |
||||||
|
|
момента — Мо. При Мо [14 Нм, 16 Нм] |
|
||||
72
11.3.Контрольные вопросы
1.Причина возникновения эффекта Зоммерфельда.
2.Негативное влияние эффекта Зоммерфельда на характеристики разрабатываемой конструкции.
3.Что характеризует зависимость амплитуды колебания двигателя от отношенияугловойскоростивалаккруговойчастотесвободныхколебанийконструкции?
4.Какиепараметры входятвуравнениевращательногодвижениястержня?
5.Каким образом получена система дифференциальных уравнений движения конструкции?
6.Этапы исследования эффекта Зоммерфельда в среде Mathcad.

73
12. ОПТИМИЗАЦИЯ РАСКРОЯ КРУГЛОГО ЛИСТА ЖЕСТИ
12.1. Основные положения и методические указания
Рассмотрим круглый лист жести радиуса R (рис. 12.1), который надо разрезать на два сектора, полученные секторы свернуть в конусы, а швы сварить. Необходимо, чтобы углы раскройки α1 и α2 обеспечили максимальный сум-
марный объем конусов [4].
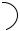
 α1
α1
R
Рис. 12.1 Лист жести, размеченный для раскроя на два сектора
Учитывая, что α2 = 2π −α1 , объемы конусов определим по формулам:
|
|
|
|
|
V = |
1 |
R3 α |
2 |
1− α12 |
|
; |
|
|
|
|
|
(12.1) |
||||
|
|
|
|
|
1 |
|
|
3 |
4π |
1 |
4π 2 |
|
|
|
|
|
|
||||
|
V2 |
|
= |
1 |
|
R3 |
|
(2π −α1 )2 |
1− (2π −α1 )2 . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
(12.2) |
||||||||||||||
|
|
|
3 |
|
4π |
|
|
|
|
|
|
|
4π 2 |
|
|
|
|
|
|||
Теперь надо выбрать значение угла α1 , при котором объем будет макси- |
|||||||||||||||||||||
мальным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V =V (α1 )=V1 +V2 = |
1 |
|
R3 |
|
2 |
1− |
α2 |
+ (2π −α) |
2 |
1 |
− |
(2π |
−α)2 |
|
(12.3) |
||||||
3 |
4π |
α |
|
|
4π 2 |
|
|
4π 2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом выражении вместо α1 |
записано α . |
|
|
|
|
|
|
|
|
||||||||||||
Таким образом, задача сводится |
|
к нахождению |
|
максимума |
функции |
||||||||||||||||
V =V (α). На угол можно наложить ограничения: |
0 <α ≤π . В этих границах мы |
||||||||||||||||||||
74
найдем α , которому будет соответствовать максимальный объем V. Второй угол, в связи с симметрией круга: α2 = 2π −α1
Многие, посмотрев на условие задачи, предполагают, что:α1 =α2 =π, но на самом деле, это неверное предположение.
12.2. Оптимизация раскроя листа жести
Дифференцируем символьно по α и находим корни полученной функции на интервале α [1,9;2,2]. Для нахождения корней используется функ-
ция root ( ).
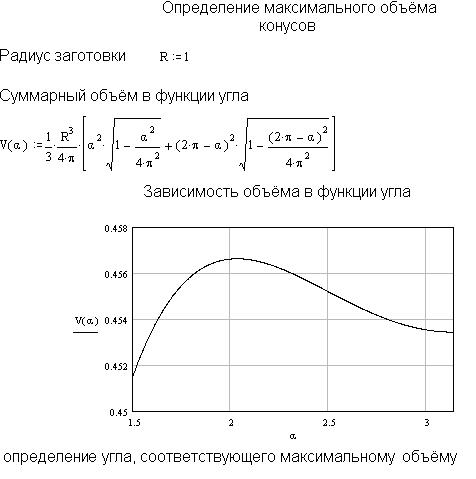
Данная задача решена с использованием пакета Mathcad (рис. 12.2-12.3). Сначала строим график функции V =V (α). Анализ графика убеждает нас, что в интервале α [1,9;2,2] имеется максимум.
Рис. 12.2 Расчет зависимости объема в функции времени

75
Рис. 12.3 Расчет угла, соответствующего максимальному объему
12.3. Контрольные вопросы
1.Как определить объемы конусов?
2.Что характеризует зависимость объема от функции угла α?
3.Как получить оптимальный угол раскроя?
4.Этапы решения задачи в среде Mathcad.
76
13. СОСТАВЛЕНИЕ ПЛАНА ПРОИЗВОДСТВА ДВУХ ИЗДЕЛИЙ, ОБЕСПЕЧИВАЮЩЕГО МАКСИМАЛЬНУЮ ПРИБЫЛЬ ОТ ИХ РЕАЛИЗАЦИИ
13.1. Основные положения и методические указания
Для производства двух видов изделий А и В используются три типа технологического оборудования. Для производства единицы изделия А оборудование первого типа используется в течении 1 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 3 часа.
Для производства единицы изделия В оборудование первого типа используется в течении 2 часа, оборудование второго типа – 3 часа, оборудование третьего типа – 1 час.
На изготовление всех изделий предприятие может использовать оборудование первого типа не более чем 32 часа, оборудование второго типа – 60 часов, оборудование третьего типа – 50 часов.
Прибыль от реализации единицы готового изделия А составляет 4 денежные единицы, а изделия В – 2 денежные единицы.
Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.
Решить задачу симплекс-методом путем преобразования симплекстаблиц. Дать геометрическое истолкование задачи, используя для этого ее формулировку с ограничениями – неравенствами [6].
13.2. Составление плана производства с использованием теории линейного программирования
Под планом производства понимается ответ на простой вопрос: сколько изделий А и сколько изделий В надо выпустить, чтобы прибыль была максимальна.
Прибыль рассчитывается по формуле: F = 4x1 + 2x2 .
|
|
77 |
|
Запишем математическую модель задачи: |
|
||
x + 2x |
|
≤ 32 |
|
1 |
2 |
|
|
3x1 +3x2 ≤ 60 |
|
||
|
|
|
|
3x1 + x2 ≤ 50 |
|
||
x1 ≥ 0 |
x2 ≥ 0 |
|
|
F(x1 , x2 ) = 4x1 + 2x2 → max |
(13.1) |
||
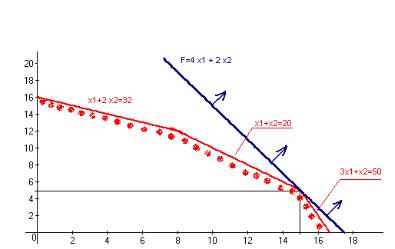
Чтобы проиллюстрировать применение симплекс-метода решения этой задачи, решим ее графически.
Для этого построим на плоскости (x1 , x2 ) области, описываемые ограни-
чениями-неравенствами, и прямую F = 4x1 + 2x2 , которая называется целевой функцией.
Три записанных выше неравенства ограничивают на плоскости многоугольник (построен красным цветом), ограниченный слева и снизу координатными осями (т.к. искомое количество изделий положительно).
График целевой функции (построен синим цветом) передвигается в направлении, обозначенном стрелкой (по-научному – в направлении своего градиента), до тех пор пока не достигнет граничной точки многоугольника – в нашем случае это точка – (15 ; 5). В этой точке целевая функция будет достигать максимума.
F (15;5) = 60 +10 = 70 |
(13.2) |
Рисунок 13.1 – График целевой функции

78
А теперь решим эту задачу симплекс-методом. Для этого перейдем от ог- раничений-неравенств к ограничениям-равенствам, введя дополнительные пе-
ременные x3 , x4 , x5 ≥ 0 .
|
|
|
x |
+ 2x |
2 |
+ x |
3 |
= 32 |
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x1 + x2 + x4 = 20 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x1 + x2 + x5 = 50 |
|
|
|
|
|
|
|
|||||||
|
|
|
xi ≥ 0 i =1..5 |
|
|
|
|
|
|
|
|||||||
|
|
|
F(x1 , x2 ) = 4x1 + 2x2 |
+ 0x3 + 0x4 |
+ 0x5 → max |
|
(13.3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 13.1 |
|
|
|
|
|
|
|
|
|
Симплекс метод |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
Cδ |
B |
|
|
|
|
4 |
|
2 |
|
0 |
|
0 |
0 |
||
|
|
|
|
|
A1 |
|
A2 |
|
A3 |
|
A4 |
A5 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
A3 |
0 |
|
|
32 |
|
|
1 |
|
2 |
|
1 |
|
0 |
0 |
|
2 |
|
A4 |
0 |
|
|
20 |
|
|
1 |
|
1 |
|
0 |
|
1 |
0 |
|
3 |
|
A5 |
0 |
|
|
50 |
|
|
3 |
|
1 |
|
0 |
|
0 |
1 |
|
4 |
|
Fi - Ci |
|
|
|
0 |
|
|
-4 |
|
-2 |
|
0 |
|
0 |
0 |
|
1 |
|
A3 |
0 |
|
|
46/3 |
|
0 |
|
5/3 |
|
1 |
|
0 |
-1/3 |
||
2 |
|
A4 |
0 |
|
|
10/3 |
|
0 |
|
2/3 |
|
0 |
|
1 |
-1/3 |
||
3 |
|
A1 |
4 |
|
|
50/3 |
|
1 |
|
1/3 |
|
0 |
|
0 |
1/3 |
||
4 |
|
Fi - Ci |
|
|
|
200/3 |
|
0 |
|
-2/3 |
|
0 |
|
0 |
4/3 |
||
1 |
|
A3 |
0 |
|
|
7 |
|
|
0 |
|
0 |
|
1 |
|
-5/2 |
1/2 |
|
2 |
|
A2 |
2 |
|
|
5 |
|
|
0 |
|
1 |
|
0 |
|
3/2 |
1/2 |
|
3 |
|
A1 |
4 |
|
|
15 |
|
|
1 |
|
0 |
|
0 |
|
-1/2 |
1/2 |
|
4 |
|
Fi - Ci |
|
|
|
70 |
|
|
0 |
|
0 |
|
0 |
|
1 |
3 |
|
Симплекс-таблица составляется так:
Вграфе Базис записываются вектора переменных, принимаемых за базисные. На первом этапе это – A3, A4, A5. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных.
Вследующий столбец Cδ записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
Под столбцом свободных членов записывается начальная оценка

79 |
|
F0 = Cδ B = 0 32 + 0 20 + 0 50 = 0 |
(13.4) |
Остальныеоценкизаписываютсяподстолбцамисоответствующихвекторов Ai .
F1 −C1 = |
Cδ |
|
A1 |
−C1 |
= 0 1+ 0 1+ 0 3 − 4 = −4 |
(13.5) |
||||
F2 −C2 = |
|
|
|
−C2 |
= 0 2 + 0 1+ 0 1− 2 = −2 |
|
||||
Cδ |
A2 |
(13.6) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
Следует отметить, что оценки для базисных векторов всегда равны нулю. Преобразование симплекс-таблицы ведется следующим образом:
Шаг 1: Проверяется критерий оптимальности, суть которого состоит в
том, что все оценки Fi |
−Ci должны быть неотрицательны. В нашем случае этот |
||||||||||||||||||||||||
критерий не выполнен, поэтому переходим ко второму шагу. |
|
||||||||||||||||||||||||
Шаг 2: Для отрицательных оценок вычисляются величины: |
|
||||||||||||||||||||||||
θ1 |
= min |
Bi |
= min |
32 |
; |
20 |
; |
50 |
= |
50 |
|
|
|||||||||||||
|
|
|
1 |
|
|
3 |
|
(13.7) |
|||||||||||||||||
|
|
|
Ai |
|
|
|
1 |
3 |
|
|
|||||||||||||||
θ2 |
= min |
32 |
; |
20 |
|
; |
50 |
=16 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
(13.8) |
|||||||||||||||
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
θ |
1 |
(F −C ) |
= |
50 |
(−4) = − |
200 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
1 |
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
(13.9) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
θ2 (F2 −C2 )=16 (−2) = −32 |
|
|
|
(13.10) |
|||||||||||||||||||||
Из этих элементов выбирается тот, для которого вычисленное произведе-
− 200
ние минимально, в нашем случае 3 минимально, поэтому в качестве так называемого разрешающего элемента выбирается третий элемент первого столбца
– 3 (выделен в таблице).
Шаг 3: Третья строка таблицы делится на 3 и вычитается из первой и второй строк. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса.
Таким образом, новыми базисными переменными становятся A3, A4, A1. Возвращаемся к шагу 1 и повторяем весь процесс.
Под столбцом свободных членов записывается начальная оценка

80
F = |
|
|
|
|
= 0 |
|
46 |
+ 0 |
10 |
+ 4 |
50 |
= |
200 |
|
|
C |
δ |
B |
(13.11) |
||||||||||||
|
|
|
|
|
|||||||||||
0 |
|
|
|
|
3 |
3 |
3 |
3 |
|||||||
|
|
|
|
|
|
||||||||||
Остальныеоценкизаписываютсяподстолбцамисоответствующихвекторов Ai .
F −C |
|
= |
|
|
|
|
|
−C |
|
= 0 |
|
5 |
+ 0 |
2 |
+ 4 |
1 |
− 2 |
|
= − |
2 |
|
|
|
|
|||||||||||
2 |
C |
δ |
A |
2 |
|
|
|
(13.12) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
2 |
|
|
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
4 |
|
||
F5 −C5 = Cδ A5 −C5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
= 0 |
|
− |
|
|
|
+ 0 |
− |
|
|
|
+ 4 |
|
|
|
− 0 |
= |
|
|
|||||||||||||||||
3 |
3 |
|
3 |
3 |
(13.13) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следует отметить, что оценки для базисных векторов всегда равны нулю. Опять проверяется критерий оптимальности. Отрицательная оценка толь-
ко одна – в столбце А2. Вычисляем:
θ2 |
= min |
46 |
;5;50 |
= 5 |
|
5 |
|||||
|
|
|
(13.14) |
Разрешающим элементом будет второй элемент второго столбца – 2/3. Новыми базисными переменными становятся A3, A2, A1. Делим вторую строку на 2 и вычитаем из третьей.
Умножаем вторую строку на 5/2 и вычитаем из первой.
F0 = Cδ B = 0 7 + 2 5 + 4 15 = 70
F1 −C1 = Cδ A1 −C1 = 0 0 + 2 0 +1 4 − 4 = 0
F2 −C2 = Cδ A2 −C2 = 0 0 + 2 1+ 0 4 − 2 = 0
F3 −C3 = Cδ A3 −C3 = 0 1+ 0 2 + 0 4 −0 = 0
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
||||
F4 |
−C4 |
= Cδ A4 −C4 |
|
|
|
|
|
|
|
|
|
− 0 |
=1 |
|||||||||||||
= 0 |
|
− |
|
|
|
+ 2 |
|
|
+ 4 |
|
− |
|
|
|||||||||||||
2 |
2 |
2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||
F5 |
−C5 |
= Cδ A5 −C5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 0 |
|
+ |
2 |
|
|
+ |
4 |
|
|
− 0 = 3 |
|
|||||||||||||||
2 |
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
На этот раз отрицательных оценок нет, т.е. критерий оптимальности выполнен.
Таким образом, получается искомое значение целевой функции F(15; 5; 7; 0; 0) = 70, т.е., возвращаясь к системе неравенств, получаем:
F (15;5) = 60 +10 = 70 |
(13.15) |
Ответы, полученные различными методами, совпадают.
