
442
.pdf
41
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.7 Зависимость силы |
|
|
|
|
|
|
Рис. 5.8– Зависимость силы резания от |
|||
|
резания от подачи на зуб |
|
|||
|
|
|
высоты пропила ствола |
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.9 Зависимость силы |
Рис. 5.10 Зависимость силы |
резания от толщины диска пилы |
резания от радиуса пилы |
|
|
|
|
|
|
Рис. 5.11 Зависимость силы резания от угла наклона зуба пилы
42
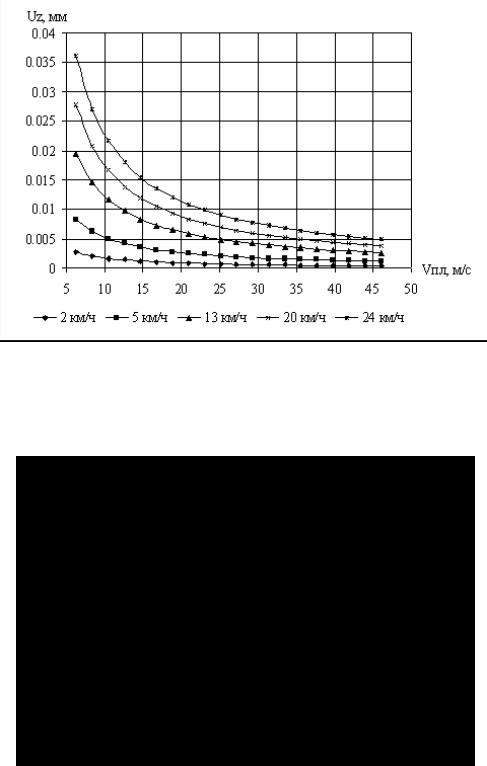
Наибольшее влияние на качество среза оказывает подача ствола на зуб пилы, поэтому необходимо построить зависимости Uz от окружной скорости пилы и скорости подачи агрегата, как это показано на рис. 5.12-5.13.
Рис. 5.12 Зависимость подачи на зуб от окружной скорости пилы при соответствующей скорости движения трактора (2, 5, 13, 20, 24 км/ч)
Рис. 5.13 Зависимость подачи на зуб от скорости движения трактора при соответствующей окружной скорости пилы (4, 13, 25, 38, 50 м/с)
43
5.3. Контрольные вопросы
1.Общий вид формулы определения силы резания.
2.Как определить дугу резания, подачу на зуб, ширину пропила?
3.Какие параметры необходимы для нахождения координат оснований и вершин зубьев дисковой пилы?
4.Почему при резании тонких стволов угол передней режущей кромки дисковой пилы не должен превышать 90°?
5.Два метода определения момента соприкоснования ствола с зубом пилы.
6.Как произвести рандомизацию стволов при известной площади рассматриваемого участка?
7.Какие параметры используются при расчете силы резания?
44
6. ОПРЕДЕЛЕНИЕ РАВНОВЕСИЯ СТВОЛА СПИЛЕННОГО ДЕРЕВА
6.1. Основные положения и методические указания
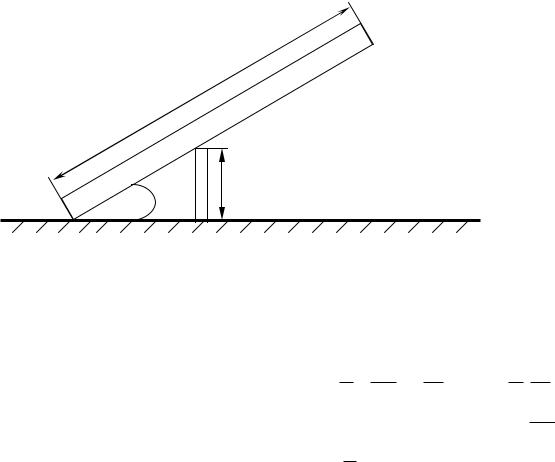
Примем допущение, что ствол очищен от веток и не имеет сбежестости тогда его можно рассматривать как однородную балку AB длиной L. Ствол на негладкую горизонтальную плоскость (почву ), а точкой D — на гладкую вертикальную опору высотой а (рис. 6.1) [4].
Коэффициент трения между балкой и плоскостью равен f.
Определить углы наклона балки, при которых она будет находиться в равновесии.
В
L
Да
α
А
Рис. 6.1 Схема к определению равновесия ствола
На основании аксиомы освобождаемости от связей, рассмотрим балку AB как свободное твердое тело, заменив действие горизонтальной плоскости и вер-
тикальной опоры соответствующими реакциями N , Fтр и N1 . Здесь N ,N1 —
нормальные реакции плоскости и вертикальной опоры, соответственно. Fтр —
сила трения скольжения. Приложим к балке вес G в ее середине — точке C. Расстояние АD обозначим d (АD=d).

|
|
45 |
y |
|
|
d |
N |
С |
1 |
|
|
|
|
G |
N |
Д |
|
|
|
|
|
α |
E |
А |
|
|
Fтр |
X |
|
Рис . 6.2 |
Силовой анализ равновесия ствола |
|
Для решения поставленной задачи достаточно написать два уравнения равновесия:
∑Fix = 0; Fтр − N1 sinα = 0;
|
|
|
|
|
|
|
|
|
|
(6.1) |
Умножив левую и правую части второго уравнения полученной системы |
||||||||||
на коэффициент трения скольжения f, приведем (6.1) к виду: |
||||||||||
Fтр = N1 sinα; |
|
|
|
|
|
|
(6.2) |
|||
f N = 2 f |
d |
|
sin2 α |
N |
|
|
d |
N |
|
cosα |
L |
cosα |
1 |
− f 1−2 |
|
1 |
|||||
|
|
|
|
L |
|
|
||||
Согласно закону Кулона (при равновесииFтр ≤ f N ), из (6.2) получим:
|
|
d |
|
sin2 |
α |
|
|
|
d |
|
|
sinα ≤ 2 |
f |
|
|
|
|
− f 1 |
−2 |
|
|
|
cosα |
L |
cosα |
|
|||||||||
|
|
|
|
|
|
L |
|
||||
или L sinα cosα + f cos2 α ( L − 2 d ) − 2 f d sin2 α ≤ 0 . (6.3)
Учтем, что d [α;L], а угол α определяется из выражения:
α= arcsin a
d
Теперь задача сведена к нахождению корней уравнения
Z(d )= L sinα cosα + f cos2 α(L −2d )−2 f d sin2 α = 0
и его графическому анализу на интересующем нас интервале изменения d.
46
6.2. Расчет равновесия ствола спиленного дерева
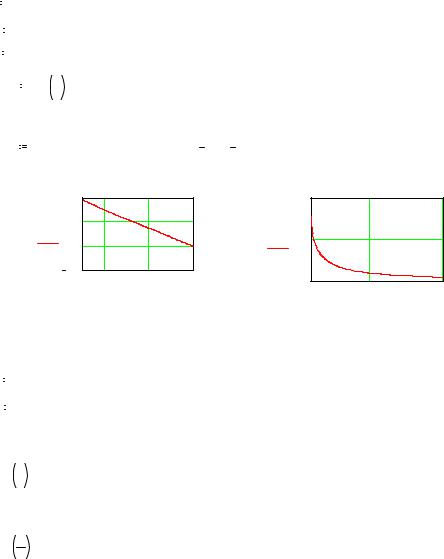
Решение с использованием Mathcad состоит в построении графиков функций Z=Z(d) и α = α( d ), рисунок 6.3. Там где Z(d)≤0 — равновесие. Значе-
ния корней уравнения Z(d)=0 определятся с помощью функции MathCAD root ( ).
Определение углов наклона балки
Исходные данные:
f |
|
|
|
0.1 |
|
|
- коэффициент трения скольжения; |
||||
|
|
|
|
|
|||||||
L |
|
|
|
|
1 |
|
-длина балки; |
||||
|
|
|
|
|
|||||||
a |
|
|
0.1 |
|
-высота опоры; |
||||||
|
|
||||||||||
α ( d ) |
|
asin |
|
a |
-функция угла наклона балки; |
||||||
|
|
|
|||||||||
|
|
|
|||||||||
d
Функция, позволяющая определить
Z ( d ) L .sin ( 2 .α ( d ) )  2 .f .d .cos ( α ( d ) ) 2 .( L
2 .f .d .cos ( α ( d ) ) 2 .( L
График функции Z=Z(d)
0.2 |
|
|
Z( d ) |
|
|
0 |
|
|
0.2 |
0.8 |
1 |
0.6 |
||
|
d |
|
углы наклона балки |
: |
|
|
2 .d ) 2 .f .d .sin ( α ( d ) ) 2 |
|
|
|
График функции |
α=α(d) |
||
|
2 |
|
|
α( d ) |
1 |
|
|
|
0 |
0.5 |
1 |
|
|
||
|
|
|
d |
Использование функции root( ) для нахождения корней уравнения
|
|
|
|
|
|
|
|
Z(d)=0 |
|
|
d |
|
|
5 |
|
- начальное приближение; |
|
|
|||
|
|
|
|
|||||||
D |
|
|
root ( Z ( d ) , d ) |
- корень; |
|
|
||||
|
|
|
|
|||||||
D = |
|
|
|
|
|
-значения корня; |
|
|
||
asin |
|
|
a |
= |
|
-минимально возможный угол; |
π |
-максимально возможный угол; |
||
|
|
|
|
|
L |
|
|
2 |
|
|
Углы, соответствующие корням:
asin D = L
Рис. 6.3 – Определение равновесия дерева средствами Mathcad
6.3. Контрольные вопросы
1.От каких параметров зависит равновесие спиленного ствола?
2.Напишите закон Кулона для равновесия тел.
3.Каким образом определяется угол наклона ствола?
4.Чему равен минимальный и максимально возможный угол наклона
ствола?

47
7. ОПРЕДЕЛЕНИЕ УСИЛИЙ В ОПОРНЫХ СТЕРЖНЯХ ПРОСТРАНСТВЕННОЙ КОНСТРУКЦИИ
7.1. Основные положения и методические указания
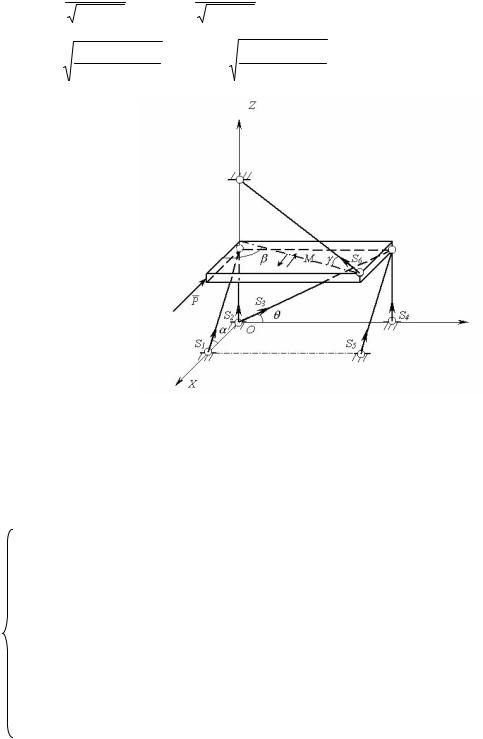
Однородная невесомая прямоугольная плита удерживается в горизонтальном положении шестью невесомыми стержнями (рис. 7.1) [4].
В точке A на плиту действует сила P и пара сил с моментом M. Определить усилие в стержнях. Толщиной плиты пренебречь.
Рис. 7.1 Однородная невесомая плита
Мысленно отбросим связи-стержни и заменим их действие шестью реак-
циями: S1 ,S 2 ,S 3 ,S 4 ,S 5 ,S 6 .
Под действием силы P , пары сил с моментом M и S1 ,S 2 ,...,S 6 плита на-
ходится в равновесии (рис. 7.2).
Для упрощения записей введем углы: α, β, γ, θ и вычислим их функции:
sinα = |
c |
; |
cosα = |
b |
c2 +b2 |
c2 +b2 |
|||
sinθ = |
c |
; |
cosθ = |
a |
a2 + c2 |
a2 + c2 |
|||
|
|
|
|
(7.1) |
|
|
|
|
48 |
sin β = |
a |
; cos β = |
b |
|
a2 +b2 |
a2 +b2 |
|||
sin γ = |
d |
+ d 2 ; cos γ = |
a 2 + b2 |
|
a 2 + b2 |
a 2 + b2 + d 2 . |
|||
Рис. 7.2 Плита находящаяся в равновесии
Запишем уравнение равновесия для произвольной пространственной системы сил:
∑x = −S1 cosα − S5 cosα − S6 cosγ cos β − P = 0 ; |
|
∑y = S3 cosθ − S6 cosγ sin β = 0 ; |
|
∑z = S1 sinα + S2 + S3 sinθ + S4 + S5 sinα + S6 sinγ =0 ; |
(7.2) |
∑M x =S4 a + S5 sinα a + S6 (sinγ a +cosγ sin β c ) =0 ;
∑M y =S1 sinα b + S5 sinα b + S6 (sinγ b + cosγ cos β c ) + P c = 0 ;
∑M z = S5 cosα a + M =0 .
7.2. Нахождение усилий в опорных стержнях
Эту задачу можно решить и без использования компьютера. Достаточно было бы упростить систему уравнений, выбирая оси координат эффективнее. Решение системы (7.2) с помощью Mathcad показано на рис. 7.3

49
Рис. 7.2 Расчет усилий в стержнях средствами Mathcad
7.3. Контрольные вопросы
1.Как рассчитать и с какой целью в модель вводятся углы α, β, γ, θ ?
2.Каким образом составлено уравнение равновесия?
3.Как составлена матрица коэффициентов уравнения равновесия?
50
8. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ РОЛИКА ТОЛКАТЕЛЯ КУЛАЧКОВОГО МЕХАНИЗМА
8.1. Основные положения и методические указания
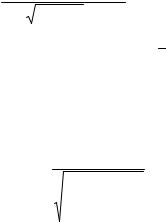
Определить перемещение ролика толкателя кулачкового механизма, изображенного на схеме (рис 8.1), в функции угла поворота кулачка. Контуром кулачка является эллипс, уравнение которого задается зависимостью [4]:
x2 |
+ |
y2 |
= 1 |
, |
(8.1) |
|
a2 |
b2 |
|||||
|
|
где a=0,04 м; b=0,035 м.
Эллипс вращается вокруг одного из полюсов.
Изобразить контур кулачка в полярных координатах ρ=ρ(ϕ) и определить крутящий момент, приложенный к кулачку, по усилию в толкателе. Это усилие задано зависимостью:
R =105 ( z + r )2 , |
(8.2) |
где z — перемещение ролика толкателя; r=0,02 м — радиус ролика толкателя.
В полярных координатах уравнение эллипса имеет вид:
|
b2 |
|
|
|
|
|
|
|||
ρ = a + a2 −b2 cosϕ . |
|
|
|
(8.3) |
||||||
Угол между вектором |
ρ |
(ϕ ) и касательной к контуру в точке контакта ку- |
||||||||
лачка и ролика толкателя можно определить по формуле: |
|
|||||||||
|
|
|
dρ |
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
dϕ |
|
|||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
µ = arccos |
dρ |
2 |
|
2 |
|
|||||
|
|
|
|
|
+ ρ |
|
|
|||
|
|
|
||||||||
|
dϕ |
|
|
|
(8.4) |
|||||
|
|
|
. |
|||||||
Рассмотрим ∆ OAO1 |
и запишем два соотношения, выражающие теорему |
|||||||||
синусов и тот факт, что сумма углов в треугольнике равна π : |
|
|||||||||
