Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

442

.pdf

Скачиваний:

Добавлен:

11.04.2015

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Таблица 2.3

Результат расчета кинематики гибкого рабочего органа

k0	k1	k2	k3	k4

	Находим	вектор	длины

xk	= rk sin(ωk t)															-0,06	-0,20	-0,42		-0,69	-0,96
																-0,06	-0,20	-0,42		-0,69	-0,96
yk	= yk cos(ωk t)															0,19	0,34	0,43		0,41	0,28
																0,19	0,34	0,43		0,41	0,28
zk	= rk Koeff sin(ωбиенk										t)					0,00	0,16	0,24		0,32	0,40
																0,00	0,16	0,24		0,32	0,40
																	Находим проекции этих
																		координат
X k	= xk cos(ωk −1 t −ωk										t)					-0,06	-0,20		-0,41	-0,67	-0,93
																-0,06	-0,20		-0,41	-0,67	-0,93
Yk	= yk cos(ωk −1 t −ωk t)															0,19	0,33		0,41	0,40	0,27
																0,19	0,33		0,41	0,40	0,27
Zk	= zk cos(ωбиенk −1 t −ωбиенk													t)		0,00	0,01		0,24	0,32	0,40
																0,00	0,01		0,24	0,32	0,40
Gip _ XYk				=		( X k				− X k −1 )2 + (Yk					− Yk −1 )2
																0,2	0,200		0,227	0,256	0,290
Gip_XZ =Gip_XZ										+ Gip_XY 2				+(Z −Z )2
	k								k−1				k	k	k−1	0,2	0,400		0,722	0,990	1,291
																0,2	0,400		0,722	0,990	1,291
																	Находим итоговые
																	Координаты
X итог = Х			k	r					/ Gip _ XZ				k
k			k		k −1								k			-0,06	-0,197		-0,341	-0,538	-0,719
																-0,06	-0,197		-0,341	-0,538	-0,719
Y итог =Y			r		−1		/Gip _ XZ				k
k	k			k	−1						k					0,19	0,334		0,342	0,321	0,213
																0,19	0,334		0,342	0,321	0,213
Z итог = Z		k		r		−1		/ Gip _ XZ				k
k		k		k		−1						k				0,00	0,011		0,199	0,258	0,309
																0,00	0,011		0,199	0,258	0,309

На рис. 1.9 показаны в трех плоскостях положения пяти материальных точек, т.е. сам рабочий орган.

				12
	Вид Спереди - ПлоскостьXZ					Вид сбоку - ПлоскостьYZ
				0,40	0,40
				0,30	0,30
				0,20	0,20
				0,10	0,10
				0,00	0,00
-0,80	-0,60	-0,40	-0,20	-0,100,00	-0,100,00	0,10	0,20	0,30	0,40
	Вид сверху - ПлоскостьXY

				0,40
				0,30
				0,20
				0,10
				0,00
-0,80	-0,60	-0,40	-0,20	0,00

Рис 1.9 Положение гибкого рабочего органа в пространстве

Таким образом, с учетом режима работы и в рассматриваемый момент времени получено положение гибкого рабочего органа.

1.3Контрольные вопросы

1.Пояснить необходимость использования трехмерной системы координат при составлении математической модели.

2.Что даёт и как рассчитывается коэффициент масштабирования rk/Rk ?

3.Как задать в модели режим работы ротора (ускорение, разгон, холостой

ход)?

4.За счет чего, рабочая зона захвата остается постоянной?

2. ИССЛЕДОВАНИЕ ПЕРЕРЕЗАНИЯ СТЕБЛЯ ЛЕЗВИЕМ

2.1. Основные положения и методические указания

При углублении лезвия в слой материала толщиной h (рис 2.1) на величину hсж, когда на его режущей кромке возникает разрушающее контактное на-

пряжение σр, начинается процесс резания. На нож действуют следующие силы: Ррез – сопротивление разрушению материала под кромкой лезвия, направленное вверх; Робж – силы обжатия материалом, имеющие горизонтальные направления и действующие на боковые грани лезвия (возникают они от расширения слоя материала, вызванного внедрением в него клина лезвия); Рсж – сопротивление слоя сжатию фаской лезвия, направленное вверх [1].

а) сопротивления, возникающее при

б) схема к определению усилий Рсж и Робж

внедрении лезвия в поросль;

Рис. 2.1 Силовое взаимодействие лезвия с материалом

Таким образом, на фаску лезвия действует сила N, являющаяся суммой проекций сил Робж и Рсж на направление нормали. От нормальной силы N на фаске лезвия возникает сила трения Т2=Nf. Аналогичная сила трения Т1 возни-

кает на другой грани лезвия силы Робж . Т1=Робж f. Вертикальная проекция силы T2′ = T2 cosβ. Подставив значение N, получим

		1	sin 2β + P	cos2		(2.1)
T ′ = f P			sin 2β + P	cos2	β .	(2.1)
2	сж 2		обж

В момент начала резания критическая сила Ркррез, приложенная к ножу, должна преодолеть сумму всех сил, действующих в вертикальном направлении,

т.е.
Ркр рез = Ррез + Рсж +Т1 +Т2′	(2.2)

Внашем случае сила Рсж относится к площади и зависимость между εсж и

σподчиняется степенному закону εсж E = σn .

Получаем Рсж

n tg(β)

(2.3)

сж

1 +

сж

Сила обжима выражается аналогично:

= µ

(2.4)

обж

1 +

сж

Подставляя значения всех сил, противодействующих Ркррез, получим значение последней

						1			1
			1			Е		1+
							n
							n
Pкр		= ∆l δ σР +						hсжn [tg(β) + f sin2 (β) + µ( f + cos2 (β)], (2.5)
Pкр	рез	= ∆l δ σР +		1				hсжn [tg(β) + f sin2 (β) + µ( f + cos2 (β)], (2.5)
	рез		1 +	1	h
			1 +	т
				т
где		∆l – длина рабочего органа, соприкасающегося с порослевиной;

δ- ширина рабочего органа;

Е– модуль деформации;

µ- коэффициент Пуассона;

ϕ - угол трения;

β - угол наклона фаски, рад;

f – коэффициент трения массы о материал лезвия, f=tg ϕ.

2.1. Пример расчета влияния геометрических параметров режущего элемента на силу резания ствола

Определить влияние угла наклона фаски β, геометрических параметров режущего элемента ∆l, δ на силу резания ствола

Расчёт выполнить для h=0,4; 1,2; 2; 2,4; 3.2 см

Константы Е=5000 Па; µ=0,14; ϕ=45°; m=1; n=1; σр=24 106 Па. Переменные ве-

личины β=30…85°; ∆l=2…5 см;

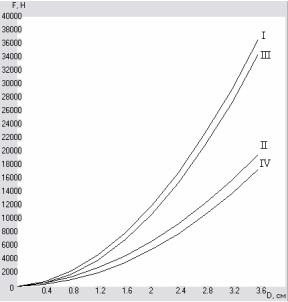
Рис. 2.2 Зависимость силы резания от диаметра поросли

δ=0,4…1 см На рис. 2.1 показана зависимость

силы резания от диаметра поросли для четырех случаев (I - δ=0,01 м, β=85°; II - δ=0,005 м, β=85°; III - δ=0,01 м,

β=45°. IV - δ=0,005 м, β=45°).

На основании полученной зависимости установлено, что толщина лезвия оказывает большее влияние на снижение силы резания, чем его заточка.

1.3.Контрольные вопросы

1.Какие силы действуют на лезвие при его внедрении в ствол?

2.Что оказывает большее влияние на силу резания – угол заточки лезвия или его толщина?

3.От каких физико-механических параметров древесины зависит сила ре-

зания?

4.При одинаковой длине режущего элемента, но разных диаметрах перерезаемого ствола Pкр будет различной?

3. ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ ПРОЦЕССОВ В ГИДРОПРИВОДЕ КУСТОРЕЗА С ГИБКИМИ ИНЕРЦИОННО-РУБЯЩИМИ РАБОЧИМИ ОРГАНАМИ

3.1. Основные положения и методические указания

Для описания работы гибкого инерционно-рубящего рабочего органа применим известное из теоретической механики дифференциальное уравнение

вращения твёрдого тела вокруг неподвижной оси [1, 2]
J пр	dω	= M дв − M c ,	(3.1)
	dt

где ω - угловая скорость вала гидромотора, с-1;

Мдв - момент, развиваемый гидромотором, Н м;

Jпр - приведенный момент инерции вращающихся масс к валу гидромотора рассчитываем по формуле Jпр = kp Jд + Jэл, кг м2;

кр - коэффициент, учитывающий вращающиеся массы редуктора;

Jд - момент инерции роторной группы гидромотора, кг м2;

Jэл - момент инерции гибкого рабочего органа, кг м2;

Момент инерции в вертикальной плоскости, представляя режущий элемент как параллелепипед, находим по формуле

J		=		1	m		[l2	+δ 2 ],	(3.2)
	Z		12			эл

где l – длина элемента, м;

δ - толщина элемента, м;

mэл – масса элемента гибкого рабочего органа mэл=ρ V, кг;

ρ - плотность материала, из которого изготовлен режущий элемент, кг/м3; V – объём режущего элемента, м3.

Используя теорему Штейнера, из формулы (3.2) находим момент инерции режущего элемента относительно оси вращения вала

17
J эл = J Z + mэл R2 ,			(3.3)
где R – расстояние от оси вращения элемента до оси вращения вала, м.
Момент, развиваемый гидромотором, вычисляется по формуле
Мдв =	ηn qм∆p	,	(3.4)

2πηo

где ηn - полный КПД гидромотора;

ηo - объёмный КПД гидромотора;

qм - удельный объём гидромотора, м3/об;

∆p - перепад давлений масла между полостями нагнетания и слива гидро-

мотора, то есть
∆p = p1 − p0 ,	(3.5)

где р1 - давление масла в полости нагнетания гидромотора, МПа;

ро - давление масла в полости слива гидромотора, МПа.

Значения давлений масла можно определить из уравнения постоянства

расхода масла, подаваемого в гидромотор от насоса	р1 и ро , выходящего из
гидромотора на слив.
Момент нагрузки на валу гидромотора, создаваемый силами сопротивле-
ния резанию, для инерционно-рубящего органа равен:
M c =εуд Jэл ,	(3.6)
где εуд – угловое ускорение удара, с-2.

Из теории импульсного резания известно, что усилие импульсного резания можно выразить из усилия «силового» резания Fл, введя поправочный совокупный коэффициент динамичности по усилию резания КДР

FДИН = FЛ КДР .

(3.7)

А из теоретической механики известно, что импульс силы выражается формулой

− FДИН	=	mЭЛ R (ωдо. уд −ωп. уд )	,	(3.8)

		t уд

где ωдо.уд. – угловая скорость рабочего органа до удара, с-1;

ωп.уд. – угловая скорость рабочего органа после удара, с-1; tуд – момент времени, в течение которого произошёл удар, с.

Тогда ускорение, получаемое режущим элементом в результате взаимодействия с порослью, вычисляем по формуле

ε уд =	ωп. уд −ωдо. уд	=		FДИН		.		(3.9)
	t уд
				m R
Подставим это ускорение в формулу (3.6), получим искомый момент, соз-
даваемый на валу от сил резания
	Мс =		FДИН		J		эл .	(3.10)

			m R

Подставив найденные выражения Мдв и Мс в исходное уравнение (3.1), получим дифференциальное уравнение движения гибкого рабочего органа с приводом от гидромотора

dω

−

FДИН

(3.11)

пр dt

m R

эл

2πη

Для возможности более полного исследования динамических процессов в рассматриваемом гидроприводе уравнение (3.11) должно быть дополнено вторым дифференциальным уравнением, которое будет описывать расход рабочей жидкости. Это уравнение имеет вид

dp	=	1	(qнωн − qмω− ay p),	(3.12)
dt
		K(p )

где К(р) - коэффициент податливости упругих элементов гидропривода; qн - рабочий объём насоса, м3/об;

qм - рабочий объём гидромотора, м3/об;

ωн – угловая скорость вращения насоса, с-1;

ω - угловая скорость вращения вала гидромотора, с-1;

аy - коэффициент утечек.

При моделировании динамических процессов в рассматриваемом гидроприводе уравнения (3.11) и (3.12) рассматриваются совместно как система, то есть

dp	=	1

		K(p )
dt
		1
dω	=
			Jпр

dt

(qнωн −qмω −ay p);

η	q		p		1		FДИН J		(3.13)
				−				эл	.
n		м
					J		m R
2πηo						пр

Система (3.13) представляет собой систему дифференциальных уравнений первого порядка, которая математически описывает динамические процессы в рассматриваемом гидроприводе.

Решим эту систему уравнений.

Для простоты записи решения произведем замену:

b =

; c =

FДИН

J эл

d =

e =

f =

;

н н

;

J пр

2πηo

J пр

K( p)

Тогда получим систему уравнений в следующем виде:

= d − e ω − f p,

(3.14)

dω

= b p − c.

Решаем первое уравнение системы:

d 2 p

= −e

dω

− f

;

(3.15)

dt2

Подставим в уравнение (3.15) второе уравнение системы (3.14):

d 2 p

= e (b p − c) − f

;

(3.16)

dt2

d 2 p

+ f

+ b e p = e c .

(3.17)

dt2

Заменим: e c = z; be = g , тогда

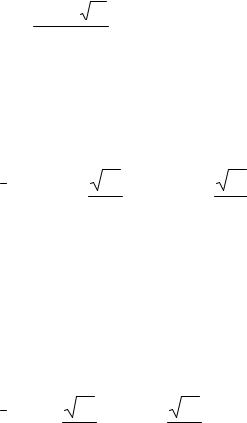
			20
d 2 p	+ f	dp	+ g p = z.	(3.18)
dt 2	+ f	dt	+ g p = z.	(3.18)
dt 2		dt

Для решения данного дифференциального уравнения отбросим правую часть и возьмем порядок дифференциального уравнения как степень некоторого числа y, получим

y2 + fy + g = 0; D = f 2 − 4g;

y	= − f ± D .	(3.19)
1,2	2
	2

Опытным путем установлено, что значение дискриминанта D меньше нуля. Из высшей математики, с учетом этого, известно, что уравнения (3.18) дают предварительный ответ:

D t) +C2

D t)).

pо

= е−

2t (C1 cos(

sin(

(3.20)

Найдем константы C1 и C2 , если известны граничные условия ωo

t=0

= 0 :

C1 +C2 = 0 C1 = −C2 .

Пусть C2 =1, значит C1 = −1. Подставив полученные значения C1

и C2 в

(3.20), получим

= е−

D t) −cos(

D t)).

pо

2t (sin(

(3.21)

Вернемся к правой части уравнения (3.18), пусть

Ω = А - в соответствии с уравнением, тогда Ω =

0; Ω = 0.

Подставим значения Ω в (3.18):

gA = z

A =

;

Ω = A Ω =	z	.	(3.22)

	g

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.04.2015773.72 Кб241529.pdf
#
11.04.2015912.61 Кб241529.pdf
#
11.04.2015190.58 Кб61533.pdf
#
11.04.2015943.86 Кб11370.pdf
#
11.04.2015154.11 Кб84243.doc
#
11.04.20151.17 Mб10442.pdf
#
11.04.2015212.95 Кб9473_2.pdf
#
11.04.2015274.56 Кб21493.pdf
#
11.04.2015483.33 Кб684_Ramnye_pily.doc
#
11.04.2015924.13 Кб844_Tekhnologicheskie_protsessy_to_i_tr.docx
#
06.05.2015896.48 Кб22529.pdf