3. Методическое и материально-техническое обеспечение

3.1. Методические указания по выполнению лабораторной работы – по числу студентов, присутствующих на занятиях.

3.2. Раздаточный материал (индивидуальные исходные данные, персональный компьютер для выполнения вычислений с использованием EXCEL) — по числу студентов.

Лабораторная работа №3 Численное интегрирование Вычисление простых интегралов ms excel

1. ЦЕЛЬ РАБОТЫ:приобрести навыки определения простых интегралов посредствам. Познакомить учащихся с применением компьютеров в качестве помощников при решении уравнений.

2. Содержание работы

2.1 Ознакомиться с теоретическими предпосылками изложенными в данной лабораторной работе, углубить знания с использованием дополнительной литературы

2.2 Изучить и разобрать пример расчета.

2.3 Для исходных данных индивидуального задания выполнить расчеты.

2.4. Выполнить анализ результатов и сделать выводы

Формула трапеций

В общем виде формула трапеций на отрезкевыглядит следующим образом (1):

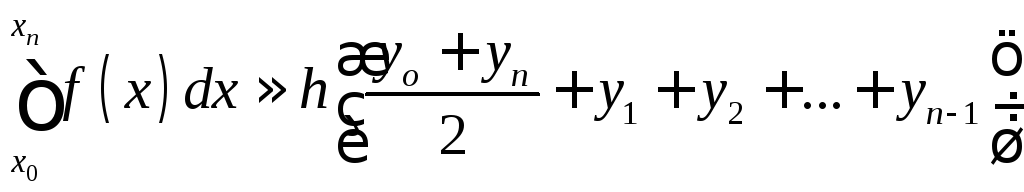
В данной формуле , так как любой интеграл в общем виде выглядит (2):

h можно вычислить по следующей формуле: (3).

это значения соответствующей функции f(x) в точках.

На практике данный способ реализуется следующим образом:

(примерMSExcelнаходится в компьютерном классе кафедры)

Формула Симпсона (парабол)

В общем виде формула парабол на отрезке выглядит следующим образом (4):

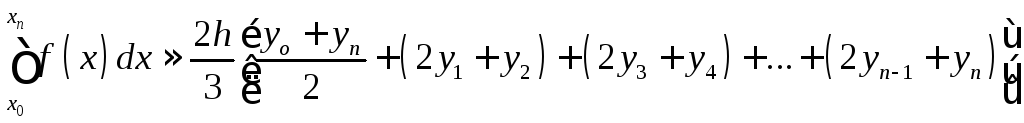
В данной формуле , так как любой интеграл в общем виде выглядит: (см. формулу 1).

h можно вычислить по формуле 2.

- это значения соответствующей функции f(x) в точках .

На практике данный способ реализуется следующим образом:

(примерMSExcelнаходится в компьютерном классе кафедры)

Формулы прямоугольников

Существует несколько видов формул прямоугольников:

Формула левых прямоугольников.

В общем виде формула левых прямоугольниковна отрезкевыглядит следующим образом (5):

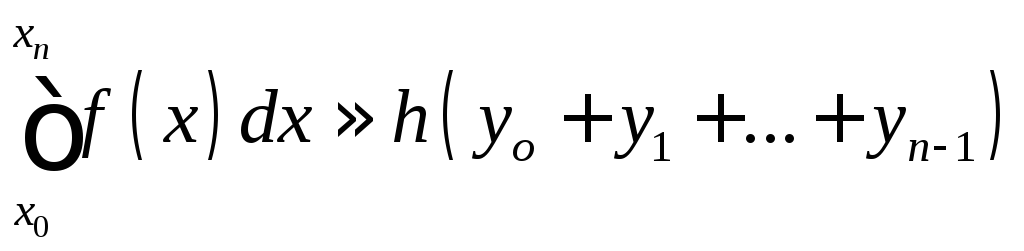
В данной формуле , так как любой интеграл в общем виде выглядит: (см. формулу 1).

h можно вычислить по формуле 2.

- это значения соответствующей функции f(x) в точках.

Формула правых прямоугольников.

В общем виде формула правых прямоугольниковна отрезкевыглядит следующим образом (6):

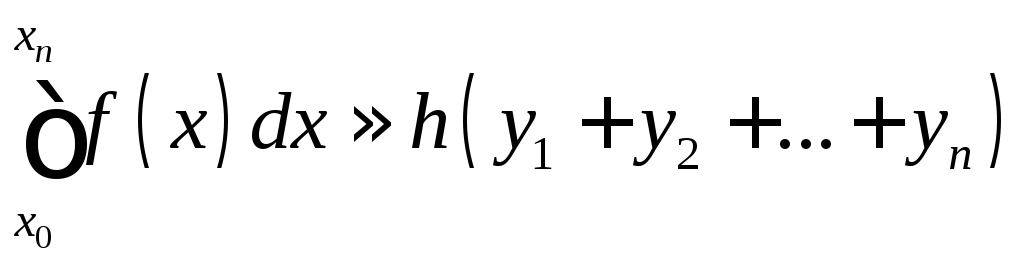
В данной формуле (см. формулу для левых прямоугольников).

h можно вычислить по той же формуле, что и в формуле для левых прямоугольников. 

- это значения соответствующей функции f(x) в точках.

Формула средних прямоугольников.

В общем виде формула средних прямоугольниковна отрезкевыглядит следующим образом (7):

где 

В данной формуле, как и в предыдущих, требуется h умножать сумму значений функции f(x), но уже не просто подставляя соответствующие значения в функцию f(x), а прибавляя к каждому из этих значений, а затем только подставляя их в заданную функцию.

h можно вычислить по той же формуле, что и в формуле для левых прямоугольников.

На практике данные способы реализуются следующим образом:

(примерMSExcelнаходится в компьютерном классе кафедры)

3. Методическое и материально-техническое обеспечение

3.1. Методические указания по выполнению лабораторной работы – по числу студентов, присутствующих на занятиях.

3.2. Раздаточный материал (индивидуальные исходные данные, персональный компьютер для выполнения вычислений с использованием EXCEL) — по числу студентов.

Лабораторная работа №4

Безусловная однопараметрическая оптимизация

задача оптимального раскроя бревна на брус

1. ЦЕЛЬ РАБОТЫ:ознакомится с методамирешения нелинейных уравнений на примере метода Свенна и применения его при оптимизации раскроя бревен.

2. СОДЕРЖАНИЕ РАБОТЫ

2.1 Ознакомиться с теоретическими предпосылками изложенными в данной лабораторной работе, углубить знания с использованием дополнительной литературы.

2.2 Изучить и разобрать пример расчета.

2.3 Для исходных данных индивидуального задания выполнить расчеты.

2.4. Выполнить анализ результатов и сделать выводы

Несмотря на то, что безусловная оптимизация функции одной переменной - наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точки зрения. Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итерактивных процедур многопараметрической оптимизации.

Пример. Постановка задачи оптимального раскроя бревна на брус

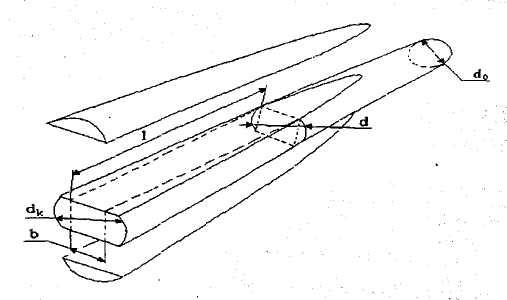
Бревно длиной 1₆м имеет форму конуса, диаметры оснований которого равны соответственноd_kиd₀м. Требуется автоматизировать процесс раскроя бревна дляполучения бруса квадратного поперечного сечения, ось которого совпадала бы с осью бревна и объем которого был бы наибольшим. Определить размеры бруса (рис.1).

Постановка задачи

1. В качестве показателя эффективности целесообразно использовать объембруса, м³.

В качестве управляемой переменной задачи следует взять длину бруса. При этом длина брусасвязана с поперечным размеромследующими зависимостями:

где –диаметр бревна вкомле, м; –диаметр бревна ввершине, м; –длина бревна, м. 3. Целевая функция:

Методы поиска, которые позволяют определить оптимум функции одной переменной путем уменьшения интервала поиска, носят название методов исключения интервалов.

Все методы одномерной оптимизации основаны на предположении, что исследуемая целевая функция в допустимой области, по крайней мере, обладает свойством унимодальности, так как для унимодальной функции сравнение значенийв двух различных точках интервала поиска позволяет определить, вкаком из заданных двумя указанными точками подынтервалов точки оптимума отсутствуют.

Правило исключения интервалов. Пустьунимодальна на отрезке [а,b], а ее минимум достигается в точке. Рассмотрими, расположенные.

Если , то точка минимумане лежит в интервале, т.е..

Если , то точка минимумане лежит винтервале , т.е..

Это правило позволяет реализовать процедуру поиска путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается тогда, когда оставшийся подынтервал уменьшается до достаточно малых размеров.

Главное достоинство поисковых методов - они основаны на вычислении только значений функции и, следовательно, не требуют выполнения условия дифференцируемости и записи в аналитическом виде. Последнее свойство особенно ценно при имитационном моделировании.

Процесс применения методов поиска на основе исключения интервалов включает два этапа:

• этап установления границ интервала;

• этап уменьшения интервала.

Этап установления границ интервала

Выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно используется эвристический метод, например, Свенна, в котором пробная точка определяется порекуррентной формуле

где – произвольно выбранная начальная точка;

– подбираемая величина шага.

Знак определяется путем сравнения значений,,:

• если 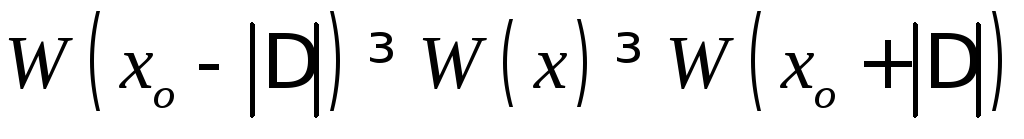, тоимеет отрицательноезначение;

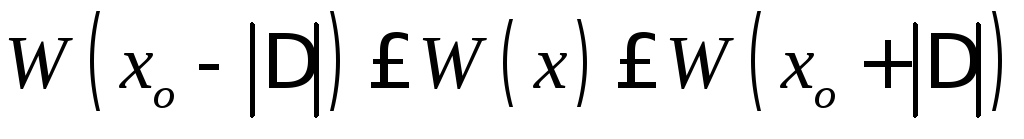• если , тоимеет положительноезначение;

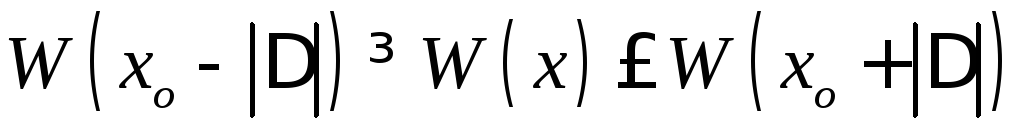• если , то точка минимума лежит между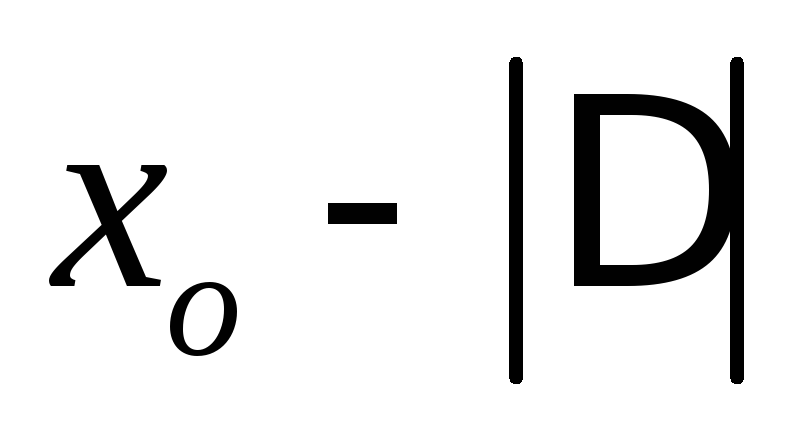ипоиск граничных точек завершен;

• если то имеем противоречиепредположению об унимодальности.

Приме. Приложение метода Свенна к задаче оптимального раскроя бревна на брус

,

при ,,,

В качестве произвольно выбранной начальной точки примем .0пределим знак:

Выполняется условие , следовательно,имеетотрицательное значение; .

;

Искомый интервал .