Связь с другими распределениями

1. При ,идействует приближённое соотношение:

Этот факт можно сформулировать в виде предельного утверждения: при всяком m=0,1,2,…

, если существует.

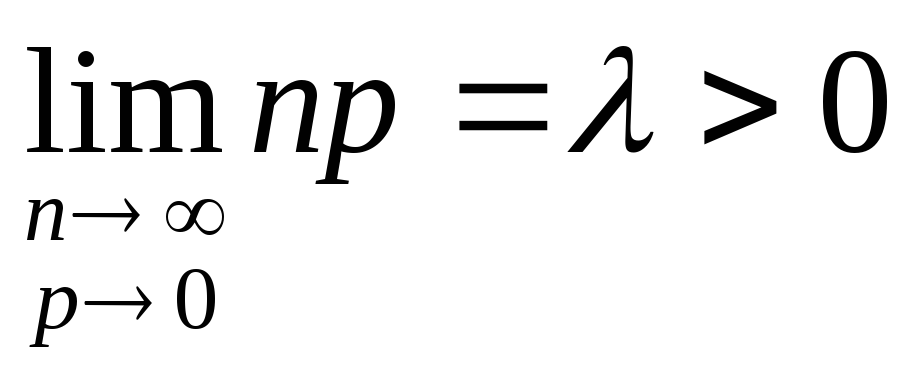Пример 3.

На изготовление 1000 булочек затрачено 5000 изюминок. Какова вероятность того, что в случайной булочке окажется менее трёх изюминок?

Решение:

Любая изюминка может с равной вероятностью попасть в каждую из 1000 булочек, т.е. вероятность попадания одной изюминки в данную булочку равна 0,001. Можно считать, что производится 5000 испытаний Бернулли, в которых решается вопрос, попадёт ли она в данную булочку. Вероятность «успеха» (попадания) p = 0,001, число испытаний n = 5000, поэтому вероятность того, что в булочке окажется менее 3-х изюминок (т.е. «или 0, или 1, или 2 изюминки») равна:

P(X<3) = P(X=0) + P(X=1) + P(X=2)

P(X<3) =

Вычисление искомой вероятности по этой формуле затруднительно. Воспользуемся приближением Пуассона (n – велико, р – мало) при λ = np = , тогда

P(X<3) = P(X=0) + P(X=1) + P(X=2) = .

Теперь по таблице распределения Пуассона имеем:

P(X<3) = P(X=0) + P(X=1) + P(X=2) = 0,0067 + 0, 0337 + 0, 0842 = 0,1246

Эти значения подчёркнуты в отрывке таблицы.

Значения функции Пуассона:.

m		1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
0		0,3679	0,1353	0,0498	0,0183	0,0067	0,0025	0,0009	0,0003	0,0001
1		0,3679	0,2707	0,1494	0,0733	0,0337	0,0149	0,0064	0,0027	0,0011
2		0,1839	0,2707	0,2240	0,1465	0,0842	0,0446	0,0223	0,0107	0,0050
3		0,0613	0,1805	0,2240	0,1954	0,1404	0,0892	0,0521	0,0286	0,0150
4		0,0153	0,0902	0,1680	0,1954	0,1755	0,1339	0,0912	0,0572	0,0337

Итак, вероятность того, что в случайной булочке окажется менее трёх изюминок равна 0,1246.

2.Например, если ДСВ Х подчиняется распределению Пуассона, то вероятность того, что Х примет значения от 8 до 12 включительно найдём по формуле

P(8X12) = P(X=8) + P(X=9) + P(X=10) + P(X=11) + P(X=12).

Теперь опишем ДСВ Х посредством НСВ Y, распределённой нормально с параметрами М(Y) =λ иD(Y) = λ. Тогда искомую вероятность можно будет найти как вероятность попадания нормально распределённой величины в заданный интервалP(7,5<X<12,5). Здесь 0,5 представляет собой поправку на непрерывность, т.к. ДСВ Х=8 в распределении Пуассона аппроксимирована интервалом 7,5 – 8,5 на непрерывной кривой нормального распределения, а ДСВ Х=12 в распределении Пуассона аппроксимирована интервалом 11,5 – 12,5 на непрерывной кривой нормального распределения.

3 Вопрос. Производящая функция.

Функция , разложение которой по степенямz (где z – произвольный параметр) даёт в качестве коэффициентов вероятности значений СВ Х, называется производящей функцией для этой СВ.

Пример 4.

В билетном зале 3 кассы. Вероятность того, что с 12 часов до 13 они работают, соответственно равны 0.9, 0.8, 0.7. Составьте закон распределения числа работающих касс в течение этого часа, и вычислите числовые характеристики этого распределения.

Решение:

СВ Х – число работающих касс в течение часа – может принимать значения 0, 1, 2, 3.

Вероятности успеха, т.е. того, что каждая из касс работает, по условию равны соответственно р₁ = 0,9; р₂ = 0,8; р₃ = 0,7. Тогда вероятности того, что каждая из касс не будет работать, равны q₁ = 0,1; q₂ = 0,2; q₃ = 0,3.

Распределение СВ Х можно получить через производящую функцию.

= (q₁ + p₁z)(q₂ + p₂z)(q₃ + p₃z) = (0,1 + 0,9z)(0,2 + 0,8z)(0,3 + 0,7z) =

= 0,504z³ + 0,398z² + 0,092z + 0,006.

Каждый из 4-х полученных коэффициентов при z^m (m = 0, 1, 2, 3) в функции выражает соответствующую вероятностьP(X=m).

Тогда распределение СВ Х – числа работающих касс – следующее:

Число успехов, X=m (xi)	0	1	2	3
Вероятности, Рn, m (pi)	0,006	0,092	0,398	0,504

0,006 + 0,092 + 0,398 + 0,504 = 1

Найдем числовые характеристики этого распределения:

- Математическое ожидание:

кассы.

Т.е. из трёх касс в билетном зале в течение следующего часа будет работать в среднем 2,4 кассы.

- Дисперсия:

Д/з – решить эту задачу, используя теоремы сложения и умножения вероятностей. Д/з – доказать, что формула Бернулли является частным случаем вычисления вероятностей Рn, m более общего способа через ПФ. См.: 2. Теория статистики с основами теории вероятностей: Учебное пособие для вузов/ И.И. Елисееева, В.С. Князевский, Л.И. Ниворожкина, З.А. Морозова; Под ред. И.И. Елисеевой. – М.: ЮНИТИ-ДАНА, 2001. – С. 111 – 114.