6.2 Программа работы

% Задать номер варианта задания

n=10;

% Определить передаточную функцию объекта, используя программу fwo6.m.

[ws,to]=fwo6(n)

% Задать время наблюдения процесса

n=100000;

dt=1; % Интервал дискретизации

t=0:dt:n-1;

% Сформировать случайный сигнал на входе

u=randn(n,1);

% Сформировать случайный сигнал на выходе

y=lsim(ws,u,t);

% Построить реализации входного и выходного сигналов их 250 значений

subplot (2,1,1)

plot (t(1:250),u(1:250)),grid

subplot (2,1,2)

plot (t(1:250),y(1:250)),grid

pause

subplot

% Рассчитать статистические характеристики входного сигнала

mu=mean(u) % Среднее значение

du=std(u)^2 % Дисперсия

ru=xcorr(u,'biased'); %Корреляционная функция

[Su,f]=psd(u,n,dt); % Спектральная плотность

% Построить график корреляционной функции для 100 значений аргумента

tau=-n+1:dt:n-1;

plot(tau(n-100:n+100),ru(n-100:n+100)),grid

pause

% Задать номер гармоники верхней частоту спектра m

m=1000;

% Построить график спектральной плотности в заданном диапазоне частот

plot(f(1:m),Su(1:m)),grid

pause

% Рассчитать статистические характеристики выходного сигнала

mu=mean(y)% Среднее значение

du=std(y)^2 % Дисперсия

ry=xcorr(y,'biased'); %Корреляционная функция

[Sy,f]=psd(y,n,dt); % Спектральная плотность

% Построить график корреляционной функции для 100 значений аргумента

plot(tau(n-100:n+100),ry(n-100:n+100)),grid

pause

% Построить график спектральной плотности в заданном диапазоне частот

plot(f(1:m),Sy(1:m)),grid

pause

% Вычислить квадрат модуля передаточной функции объекта

w=2*pi*f;

a2=abs(squeeze(freqresp(ws,w))).^2;

% Построить график квадрата модуля передаточной функции

plot(f(1:m),a2(1:m)), grid

pause

% сравнить спектры выходного сигнала и квадрата модуля W(p)

plot(f(1:m),Sy(1:m),f(1:m),a2(1:m),'r'), grid

Подпрограмма fwo6.M

% Формирование коэффициентов передаточной функции tf-модели

function [wo,to]=fwo6(n)

dan=floor(90*rand(30)+10);

to=dan(n);

wo=tf(1,[to 1]);

6.3 Порядок выполнения работы

Студент, самостоятельно изучив теоретические сведения [20], должен:

• Провести моделирование случайного процесса, используя приведенную выше программу работы.

• Определить статистические характеристики случайного процесса на входе и выходе объекта.

6.4 Контрольные вопросы

1. Какие характеристики используют для количественной оценки и сравнения различных случайных сигналов?

2. Что такое корреляционная функция?

3. Какой случайный процесс называют стационарным?

4. Какой метод моделирования случайных сигналов используют в этой работе? В чем суть этого метода?

5. Запишите формулу для вычисления спектральной плотности.

6.5 Содержание отчета

6.5.1. Название и цель работы.

6.5.2. Краткие теоретические сведения.

6.5.3. Результаты расчетов с необходимыми комментариями.

6.5.4. Листинг программы MATLAB.

6.5.5. Анализ результатов и выводы по работе.

Лабораторная работа № 7

Определение передаточной функции по временным характеристикам объекта.

Цель работы– изучение логарифмического метода определения передаточной функции по временным характеристикам объекта

7.1 Общие сведения

Рассмотрим определение передаточной функции объекта по кривой разгона логарифмическим методом. Преимущество этого метода состоит в том, что результаты идентификации получаются в виде аналитического выражения. Методика идентификации в этом случае [27] заключается в ап­прок­симации переходной характеристики аналитическим выражением типа

, (7.1)

где - коэффициент передачи объекта:– установившееся значение выходной величины объекта, соответствующее частному решению его ДУ и определяемое вынужденным движением под действием входного сигнала, остальные слагаемые определяют свободные движения и представляют общее решение однородного ДУ объекта;

С_к – постоянные интегрирования;

s_к – корни характеристического уравнения.

Положим, для определенности, что в формуле (7.1) имеется один действительный корень, два комплексно сопряженных и два кратных корня. Логарифмируя формулу (7.1) получим

. (7.2)

Для устойчивого объекта свободные движения с течением времени стремятся к нулю, причем время переходного процесса будет определяться корнем, имеющим минимальную действительную часть (например, действительным корнем). Тогда начиная с некоторого момента времени слагаемыми в выражении (7.2), имеющими большие действительные части можно пренебречь и приближенно записать:

. (7.3)

Уравнение (7.3) является асимптотой формулы (7.2) при .

Если теперь в полулогарифмическом масштабе построить график уравнения (7.2) , откладывая на оси абсцисс время на оси ординат , то неизвестные коэффициентыC₁, s₁ легко определить графически, как показано на рисунке 7.1.

Рисунок 7.1.

Ордината асимптоты при t=0 равна ln((С₁), а . После чего из уравнения (7.2) можно исключить одно слагаемое, соответствующее действительному корню, тогда

. (7.4)

Аналогично, начиная с некоторого момента времени, слагаемыми в формуле (7.4), имеющими большие действительные части, можно пренебречь и приближенно записать:

. (7.5)

Логарифмируя, получим

. (7.6)

Уравнение прямой на графике (рис.7.2), проходящей через точки, в которых имеет вид:

. (7.7)

Рисунок 7.2.

Неизвестные параметры C₂ и находятся аналогично (см.рис.7.1). Круговую частоту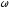и начальную фазуможно определить из очевидного условия:

, (7.8)

где t_i – значения времени, при которых ординаты переходной характеристики принимают экстремальные значения.

Минимизируя квадрат невязки (7.8) по иполучим систему алгебраических уравнений для их определения:

(7.9)

где - неизвестная частота;

- относительная фаза;

m – число экстремальных значений переходной характеристики.

Коэффициенты последних слагаемых от корней, имеющих кратность – два, в уравнении переходной характеристики (7.1) получают из выражения, аналогичного уравнению (7.4):

. (7.10)

Приближенно при больших t можно записать:

, (7.11)

где s=s₄=s₅ – корень двойной кратности.

Асимптотой этого уравнения будет прямая, тангенс угла наклона которой будет равен s.

Если теперь простроить в логарифмических координатах функцию , то ее асимптотой будет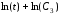. Тангенс угла наклона асимптоты дает кратность корня. Ордината асимптоты приt=0 равна ln(C₃).

Зная аналитическое выражение для переходной характеристики нетрудно определить и передаточную функцию через преобразование Лапласа:

. (7.12)

Удовлетворительные результаты при использовании этого метода получаются в том случае, если корни характеристического уравнения далеко отстоят друг от друга. Желательно, чтобы каждый следующий корень был в 2-3 раза меньше предыдущего. Следует отметить, что точность определения харак­теристик объекта с помощью временных характеристик невысока. Качество идентификации снижают случайные по­ме­хи, искажающие реакцию объекта и неточность аппроксимации объекта линейной моделью. При проведении эксперимента по снятию кривой разгона необходимо тщательно изолировать объект от случайных возмущений, стремиться, как можно точнее воспроизвести заданную форму возмущения на входе, дублировать проведение экспериментов по снятию кривой разгона для различных начальных значений y₀ и u₀.