5.2 Программы работы

% Задайте начальное значение случайного числа из диапазона [0,1]

r(1)=.1234567;

l=.01; % Параметр экспоненциального закона распределения

% По формуле (5.1) при К=37 получить 10000 чисел с равномерным законом распределения

for i=2:1000 % 1000 – число генерируемых чисел

x=37*r(i-1);

z=floor(x); % Выделение целой части числа х

r(i)=x-z;% Вычисление случайных чисел с равномерным законом

% Вычислить случайные числа с нормальным законом по формуле (5.3)

n(i)=sqrt(2*log(1/r(i)))*cos(2*pi*r(i-1));

end

% Вычислить случайные числа с равномерным законом в MATLAB

rr=rand(1000,1);

% Вычислить случайные числа с нормальным законом в MATLAB

nr=randn(1000,1);

% Вычислить случайные числа с экспоненциальным законом

ex=-log(1-r)/l;

% Вычислить случайные числа с экспоненциальным законом в MATLAB

exr=-log(1-rr)/l;

% Построить гистограммы для полученных случайных чисел

hist(r), grid% Построение гистограммы дляr

pause

hist(rr), grid% Построение гистограммы дляrr

pause

hist(n), grid% Построение гистограммы дляn

pause

hist(nr), grid% Построение гистограммы дляnr

pause

hist(ex), grid% Построение гистограммы дляex

pause

hist(exr), grid% Построение гистограммы дляexr

pause

% Проверить статистические гипотезы о равенстве законов распределения по критерию Колмогорова - Смирнова (при h=0 гипотеза принимается)

hr=kstest2(r,rr)

hn=kstest2(n,nr)

hex=kstest2(ex,exr)

% Самостоятельно по заданию преподавателя сгенерировать числа, имеющие произвольный закон распределения

5.3 Порядок выполнения работы

Студент, самостоятельно изучив теоретические сведения [12, 19], должен:

• По заданию преподавателя сгенерировать числа, имеющие произвольный закон распределения.

• Построить гистограммы случайных чисел.

5.4 Контрольные вопросы

1. Какие законы распределения случайных чисел вы знаете?

2. На какие задачи разделяется задача получения случайных чисел?

3. Какие способы используют для получения последовательности случайных чисел?

4. В чем заключается метод усечений?

5.5 Содержание отчета

5.5.1. Название и цель работы.

5.5.2. Краткие теоретические сведения.

5.5.3. Результаты расчетов с необходимыми комментариями.

5.5.4. Листинг программы MATLAB.

5.5.5. Анализ результатов и выводы по работе.

Лабораторная работа № 6

Исследование генераторов случайных сигналов на ЭВМ

Цель работы: изучить методы генерации и анализа случайных сигналов на ЭВМ.

6.1 Общие сведения

Внешние воздействия могут быть полезными (управ­ляющими сигналами u) и помехами (возмущающими воздействиями f). Выходные переменные объекта y(t) определяются не только входными сигналами x(t), но и ненаблюдаемыми и неуправляемыми воздействиями (помехами), что вызывает неконтролируемые отклонения выходных переменных от заданных зна­чений. При повторения процессов управления, происходящих в системе, выходные переменные могут иметь различные значения при одних и тех же значениях времени отсчитываемых от начала процесса. Выходная величина объекта при каждом повторном цикле управления, в этом случае, представляет собой реализацию одного и того же случайного процесса управления.

Для количественной оценки и сравнения различных случайных сигналов используют их различные характеристики:

1. Функция распределения вероятностей случайного процесса, или интегральная функция распределения. F(y,t), Функция распределения вероятностей, это вероятность того, что случайный процесс x(t) в момент времени t принимает значения меньше у:

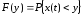. (6.1)

2. Плотность вероятностей, или дифференциальное распределение (распределение) w(x,t):

, (6.2)

откуда

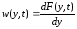. (6.3)

3. Математическое ожидание случайного процесса :

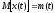. (6.4)

4. Дисперсия случайного процесса:

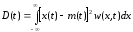, (6.5)

или . (6.6)

4. Корреляционная (автокорреляционная) функция R_xx(t₁,t₂). Корреляционная функция это математическое ожидание произведений двух значений одного и того же сигнала, сдвинутых по времени:

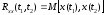. (6.7)

5. Взаимная корреляционная функция R_xy(t₁,t₂). Взаимная корреляционная функция это математическое ожидание произведений двух сигналов, один из ко­торых сдвинут относительно другого по времени:

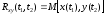. (6.8)

Точное определение этих характеристик невозможно, так как неизвестен вид закона распределения и конечное число реализаций случайного процесса. Поэтому в реальных условиях эти характеристики вычисляют приблизительно, оценивая их с какой-то погрешностью.

Оценка характеристик случайных процессов проводится на основе принятия гипотез о стационарноси и эргодичности случайного процесса.

Случайный процесс называют стационарным , если характеризующая его функция распределения не зависит от времени. Отсюда следует, что от времени не будут зависеть и все характеристики случайного процесса. Условие стационарнрсти значительно упрощает вычисление характеристик случайных процессов, так как в выражениях (6.1) - (6.8) исчезает аргумент времени. Однако и вэтом случае для вычисления характеристик необходимо достаточно большое количество независимых реализаций случайного процесса (ансамбль реализаций).

Эргодическая гипотеза позволяет заменить ансамбль реализацй одной реализацией снятой за достаточно продолжительный интервал времени. Согласно эргодической гипотезе средние значения случайного сигнала по множеству и времени совпадают:

. (6.9)

Тогда для случайных стационарных эргодических процессов оценки их ха­рактеристик выражений (6.1) - (6.8) с учетом конечности времени наблюдения Т , записыва­ются в следующем виде:

1. Оценка математического ожидания:

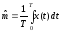. (6.10)

2. Оценка дисперсии:

(6.11)

или 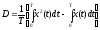. (6.12)

3. Оценка корреляционной функции:

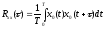, (6.13)

где - центрированный случайный сигнал.

Корреляционную функцию центрированного сигнала еще называют ковариационной или автоковариационной функцией.

4. Спектральная плотность мощности 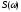, связанная с корреляционной функцией преобразованием Фуре:

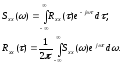(6.14)

Для получения приемлемой точности оценох характеристик случайных процессов длительность реализации процесса по которой вычисляются оценки должна превышать интервал корреляции. Интервал корреляции 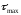ето значение аргумента корреляционной функции начиная с которого все ее последующие значения не превышают.

Одним из наиболее распространенных подходов к моделированию случайных сигналов является метод формирующих фильтров. Моделирование случайного сигнала этим методом осуществляется в предположении, что он является реакцией линейной системы на случайный входной сигнал, характеристики которого известны.

Пусть на вход линейной системы с передаточной функцией W(s) и функцией веса 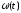действует центрированный, стационарный, эргодический, случайный сигналx(t) с известной корреляционной функцией 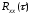и спектральной плотностью. Тогда случайный сигнал на выходе системы вычисляется с помощью интеграла Дюамеля по формуле

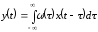. (6.15)

Умножив это выражение на сначала на x(t + ), а затем на y(t + ), и проинтегрировав обе части по в пределах от –T до T (при T  ), получим соотношения Винера - Ли:

(6.16)

Отсюда следует, что

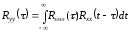, (6.17)

где

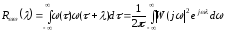. (6.18)

Эти соотношения значительно упрощаются, если представить их через спектральные плотности, используя соотношения Винера – Хинчина:

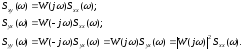(6.19)

При моделировании в качестве входного сигнала используют стационарный белый шум со следующими характеристиками:

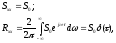(6.20)

где S₀– интенсивность белого шума.

Белый шум представляет собой сумму гармонических колебаний всех частот, имеющих одну и ту же дисперсию амплитуды. Обычно в качестве генератора белого шума используют числовую последовательность, имеющую нормальный закон распределения, привязанную к фиксированным интервалам времени.

При наличии на входе линейной системы белого шума на ее выходе формируется случайный сигнал, характеристики которого легко определяются через параметры системы с помощью формул (6.17) – (6.20):

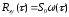; (6.21)

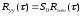; (6.22)

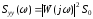. (6.23)