Лабораторная работа № 1 Создание линейных стационарных моделей систем управления и определение их свойств

Цель работы - изучение функций Control System Toolbox, предназначенных для создания линейных стационарных моделей объектов управления и определения их свойств.

1. Формы задания моделей сау в matlab

Для описания непрерывных и дискретных динамических моделей систем управления с постоянными параметрами (LTI – объектов, от англ. linear time invariant object) в системе MATLAB и, в частности, его приложении Control System Toolbox используется либо tf-форма передаточной функции, либо zpk-форма нулей, полюсов и обобщенного коэффициента передачи, либо ss-форма пространства состояний. Передаточная функция описывается в виде отношения многочленов канонического вида, которые задаются в виде векторов-строк, составленных из их коэффициентов. В zpk-форме корни многочленов числителя и знаменателя передаточной функции и обобщенного коэффициента также задаются в виде одномерных массивов. Наиболее естественным для систе­мы MATLAB является представление модели в пространстве состояний в виде дифференциального или разностного уравнения. Модели могут быть одномерными (с одним входом и одним выходом - SISO) или многомерны­ми (со многими входами и многими выходами - MIMO).

Таким образом, математическую модель стационарной непрерывной или дискретной системы можно задать следующими способами:

• в tf-форме передаточной функции:

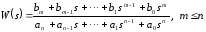; (1.1)

где 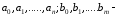постоянные коэффициенты;

n – порядок системы;

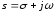- оператор Лапласа.

• в zpk-форме через нули γ_j, полюса s_i и обобщенного коэффициента K:

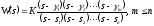; (1.2)

где m – порядок оператора входных воздействий.

• в ss-форме пространства состояний в виде системы дифференциальных уравнений, записанной в форме Коши:

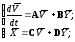(1.3)

• в модифицированной dss-форме пространства состояний в виде системы дифференциальных уравнений, записанной в неявной форме Коши:

(1.4)

Такая форма представления используется в тех случаях, когда матрица Е плохо обусловлена по отношению к операции обращения.

Ниже представлены функции MATLAB, используемые для создания LTI – моделей и определения их свойств.

Таблица 1.1 - Функции создания LTI – моделей

tf	Задает объект в форме tf
zpk	Задает объект в форме zpk
ss	Задает объект в форме ss
dss	Задает объект в форме dss

Таблица 1.2 - Функции извлечения информации об LTI – моделях

get	Информация о динамических параметрах ММ
ssdata	Извлечение данных об ss-модели в явной форме Коши
dssdata	Извлечение данных об ss-модели в неявной форме Коши
tfdata	Извлечение данных о tf-модели
zpkdata	Извлечение данных о zpk-модели

Таблица 1.3 - Преобразование LTI- моделей

c2d	Построение дискретной модели непрерывной системы
d2c	Построение непрерывной модели дискретной системы
d2d	Изменение периода дискретности
ss	Преобразование моделей к ss-форме
tf	Преобразование моделей к tf-форме
zpk	Преобразование моделей к zpk-форме

Таблица 1.4 - Переопределение базисных функций

plus	Сложение LTI-моделей
minus	Вычитание LTI-моделей
mtimes	Умножение LTI-моделей
horzcat	Горизонтальная конкатенация LTI-модели
vertcat	Вертикальная конкатенация LTI- модели
ctranspose	Переход к сопряженной LTI- модели
transpose	Транспонирование LTI- модели
inv	Инверсия LTI-модели
mrdivide	Деление моделей вида inv(a)*b
mldivide	Деление моделей вида inv(b)*a

Таблица 1.5 - Соединение lti-моделей

parallel	Параллельное соединение (сложение LTI-моделей)
series	Последовательное соединение (умножение LTI-моделей)
feedback	Соединение с обратной связью
append	Объединение LTI-моделей с добавлением входов и выходов
connect	Объединение LTI-моделей с использованием матрицы соединений
star	Объединение взаимосвязанных многомерных моделей

Подробнее о рассматриваемых функциях можно ознакомится в [3] или в справочной системе MATLAB. Для получения справки необходимо в рабочем поле MATLAB задать оператор вида help "имя функции" (напр. help ss).