4.4. Вычисление неизмеряемых величин по уравнениям регрессии (косвенные измерения)

Ввиду отсутствия надежных автоматических датчиков измере­ние многих технологических параметров в производственных условиях производится путем лабораторных анализов периоди­чески отбираемых проб. Результаты анализов обычно посту­пают с большим запаздыванием, что затрудняет их использо­вание при оперативном управлении технологическим процессом.

Вместе с тем в ряде случаев удается выявить связь между определяемой величиной и и одним или несколькими техноло­гическими параметрами, поддающимися автоматическому из­мерению. Как правило, эта связь является стохастической, т. е. описывается уравнением регрессии

,

где - условное математическое ожидание величиныиот вектора измеряемых величин ; —вектор параметров уравнения регрессии.

Определение структуры функции и ее параметров производится методами регрессионного анализа. Чаще всего встречаются линейные уравнения регрессии

. (4.51)

К этой же форме могут быть приведены некоторые уравнения другой структуры путем замены переменных или иных преобразовании. Например, полиномиальное уравнение вида

приводится к форме (4.51) заменой переменных x_i=yⁱ,. Уравнения вида

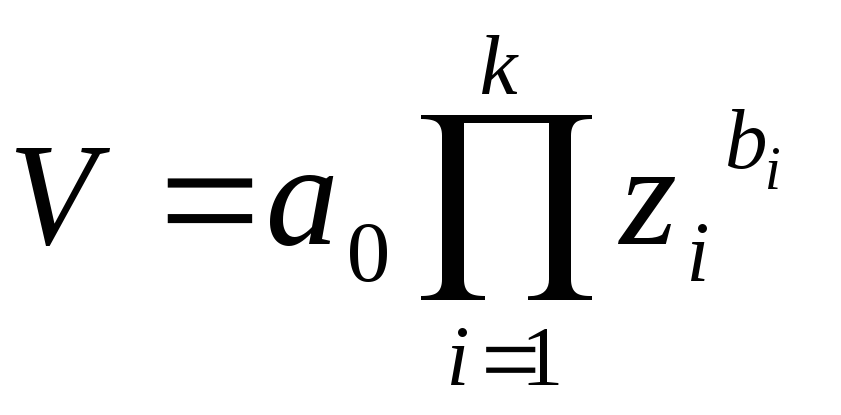
преобразуются к линейной форме (4.51) логарифмированием с последующей подстановкой =ln V; b₀=ln a₀; x_i= ln z_i.

Значения параметров уравнения линейной регрессии опре­деляют по методу наименьших квадратов, т. е. из условия

.

Методика расчета подробно изложена в литературе [24], поэтому отметим только основные ее этапы и некоторые осо­бенности.

Значения параметров рассчитывают по формулам:

b_i=|L_i|/|L|, ;

,

где т_ииm_хi,—оценки математических ожиданий величиниих_i, |L| - определитель, составленный из корреляционных функций измеряемых вели­чинпри ;|L_i| - определитель, полученный из|L| заменойi-того столбца столбцом, составленным из взаимнокорреляционных функций.

Адекватность уравнения регрессии экспериментальным дан­ным проверяют по критерию Фишера, а значимость отдельных коэффициентов - по критерию Стьюдента.

Экспериментальные данные для построения уравнения ре­грессии получают, производя синхронные измерения значений величины и и вектора . Затем эти данные используют для расчета оценок и , характеризующих степень линейной связи соответствующих величин.

Однако в общем случае все величины, участвующие в рас­четах, измеряют в разных точках объекта, т. е. они разделены динамическими каналами. Оценки величин , полученные без учета и компенсации динамических каналов, определяют не истинную степень линейной связи и с x_i, а степень линейной связи этих величин, фиксируемых в одни и те же моменты времени, которая обычно значительно слабее [24]. Поэтому для повышения точности результатов косвенных измерений при построении уравнения регрессии рекомендуется учитывать ди­намические связи между величинами и и x_i. При этом могут быть использованы любые методы приведения, изложенные в разд. 4.3.

Примером использования уравнения множественной линейной регрессии может служить метод косвенного измерения одного из показателей каче­ства полиэтилена — так называемого индекса расплава — по значениям тех­нологических параметров, измеряемых в процессе грануляции [13].

Индексом расплава, характеризующим реологические свойства полиэти­лена, а также в некоторой степени его молекулярную массу, называют ко­личество расплава полиэтилена, выдавленное из грузового пластомера через стандартное отверстие в течение 10 мин при температуре 190 °С. Длитель­ность полного цикла анализа составляет 15—20 мин, что исключает воз­можность использования результатов для автоматического регулирования. Разработанный метод косвенного измерения состоит в следующем.

В процессе работы гранулятора измеряют текущие значения давления Р, температуры  и крутящего момента М_кр на валу шнека, связанные с ин­дексом расплава F регрессионным уравнением

F=33,4 — 0,066 М_кр — 0,69Р — 0,035 . (4.52)

Подстановка измеренных значений в уравнение (4.52) позволяет рассчи­тать оценку текущего значения показателя F. Алгоритм косвенного измере­ния индекса расплава использован в составе математического обеспечения АСУТП «Полимир».