Оценка возможностей использования одноконтурных АСР.

Для выбора локальных контуров регулирования удобно результаты расчетов свести в таблицу, характеризующую возможности использования тех или иных каналов регулирования. Для каждого из управляющих воздействий u_v и регулируемых переменныху, при тех или иных типовых законах регулирования в таблицу вносят отношение а_;vрассчитанной оценкиа_у/ к допустимому отклонению. Если это отношение оказывается больше единицы, или если между управлениеми_у и переменнойу\ нет связи, ставят прочерк. Таким образом, если прочерки стоят в какой-либо строке, это значит, что данное управляющее воздействие неприменимо. Если же прочерки стоят во всех клетках некоторого столбца, это значит, что данный параметр нельзя стабилизировать с требуемой точностью с помощью одноконтурных АСР. Такие строки и столбцы на данном этапе исключаем из рассмотрения.

Наиболее простой закон регулирования — пропорциональный, поэтому в первую очередь проверяем возможность использования П-регулятора. Показателем качества регулирования в этом случае служит наибольшее из двух чисел — a/_v (отношение среднеквадратичной ошибки к максимальному допустимому ее значению) илиp_;v—отношение статической ошибки регулирования

(1.57)

к допустимому отклонению Дг//.

Таблица 1.& Показатели качества регулирования в одноконтурных АСР с П-регулятором

При подсчете статической ошибки регулирования значения каждого из возмущений Аг,- приводят ко входу канала регулирования из условия

(1.58)

и в формулу (1.57) подставляют наибольшее приведенное статическое возмущение. Такой подход правомерен, потому что вероятность статического отклонения одновременно нескольких возмущающих воздействий от номинальных значений на предельную величину очень мала.

При выборе контуров регулирования каждой из регулируемых переменных у,- нужно сопоставить одно из управляющих воздействий «_v. При этом необходимо учесть, что одно и то же управление нельзя использовать для регулирования двух или более величин. Критерием правильности выбора контуров регулирования может служить наибольшее значение показателя качества для выделенных контуров. При оптимальном выборе это значение должно быть возможно меньше.

Рассмотрим пример выбора одноконтурной АСР с П-регу-лятором (табл. 1.3). В отличие от показателей качества отдельных контуров регулирования введем показатель качества АСР процесса:

Требуется так выбрать управления щ для каждой из переменныху,-, чтобы, во-первых, значение П оказалось минимальным и, во-вторых, каждое «управление было использовано лишь для одной регулируемой величины.

Поставленная задача относится к так называемым задачам о назначениях, для решения которых при большой размерностиу и и имеется целый ряд алгоритмов, ориентированных на использование ЦВМ. Однако при небольшой размерности этих векторов приемлемое решение можно найти с использованием следующей процедуры.

1-й шаг. Выбирают начальное приближение искомого решения. Для этого временно отбрасывают второе из приведенных

требований и для каждого у,- находят управление, обеспечивающее минимальное значение показателя качества одноконтурной АСР с регулятором данного типа (в табл. 1.3 соответствующие числа отмечены звездочкой). Максимальное из отмеченных значений П* (в табл. 1.3 оно равно 0,4 и соответствует контуру г/₄~ иг) заведомо не превосходит П_тщ. Однако может оказаться, что одно и то же управление сопоставлено нескольким регулируемым переменным (в табл. 1.3 оказалось, чтои& используется для регулированияу₂ и г/₅). Если такой ситуации не возникло, найденное решение удовлетворяет условиям задачи, и П* = —llmin-

2-й шаг. Для регулируемых переменных, которым оказалось сопоставлено одно управление, ищут подходящее среди «свободных» управлений, т. е. управление, которое на первом шаге не сопоставлено ни одной из переменных г/,- и для которого показатель качества минимален. В рассматриваемом примере для г/₂и г/5 находят «свободное» управлениеи₇, которое при регулировании г/г может обеспечить показатель качества 0,4. Так как это значение не превосходит П*, задача решена, ибо показатель качества системы не ухудшился, а все ограничения выполнены.

Таким образом, структура системы определяется соответствиями г/2 — «7; г/з~«ь t/₄— «2; г/5~«₈, а Я_т1п= 0,4.

Прочерк в первом столбце табл. 1.3 говорит о том, что параметр i/iнельзя регулировать при использовании одноконтурной системы с П-регулятором. Для всех подобных переменных на следующем этапе составляют таблицу показателей качества при использовании ПИ-регулятора и аналогичным образом выбирают контуры регулирования. Затем, если необходимо, выбирают контуры регулирования с ПИД-регуляторами. Если в некоторых столбцах таблицы стоят прочерки по всем управлениям для всех типов регуляторов, значит, необходимо использовать дополнительные средства улучшения качества регулирования. Предварительный выбор схемных методов улучшения качества регулирования. Среди методов повышения качества регулирования за счет усложнения структуры систем регулирования наиболее распространены следующие:

1) введение импульса по возмущению; 2) введение динамической компенсации в системах взаимосвязанного регулирования; 3) использование каскадных АСР; 4) введение в АСР импульса по значению промежуточной координаты.

Подробно каждый из этих способов и выбор параметров корректирующих устройств изложены в разделе 1.2. Здесь мы остановимся только на возможностях предварительной оценки полезности использования схемных методов повышения качества при выборе структуры системы.

Введение в систему регулирования импульса по возмущению целесообразно в том случае, если показатель качества а при выборе любого из типовых законов регулирования для данного

параметра оказался больше единицы, причем в формуле (1.54) для расчета среднеквадратичной величины приведенного возмущения доминируют одно или два возмущающих воздействия, которые доступны прямому или косвенному измерению. Такое введение полезно и тогда, когда одно из доступных измерению возмущений имеет значительное статическое отклонение Аг. При правильном выборе характеристик динамического компенсатора (см. разд. 1.2) их влияние существенно уменьшается, и соответствующие слагаемые в уравнении (1.54) можно исключить. Показатель качества регулирования при этом уменьшится (если он станет меньше единицы, соответствующее значение можно подставить в таблицу и использовать при дальнейшем анализе).

В системах с взаимосвязанными параметрами регулирующие воздействия влияют не только на «собственную», но и на другие регулируемые переменные, являясь для них дополнительными возмущениями, которые следует учитывать при расчете показателей качества регулирования а и р. Если вклад этих возмущений в среднеквадратичную ошибку значителен и показатель качества регулирования больше единицы, нужно ввести динамические компенсаторы, т. е. перейти к системе автономного регулирования.

- Если после компенсации влияния возмущений для регулирования некоторых параметров нельзя использовать одноконтурную систему (т. е. соответствующие таблицы остались незаполненными), целесообразно оценить возможности каскадной АСР (рис. 1.53). В этой системе (см. разд. 1.2.2) вспомогательный регулятор поддерживает на заданном уровне промежуточный параметр г/„_ьа основной регулятор меняет задание вспомогательному так, чтобы стабилизировать регулируемую величинуу_ч.

При использовании каскадной АСР возмущающие воздействия z, влияющие нау ₇через изменениеу_у гасятся во внутреннем контуре. Требования к статической ошибке поддержанияy_Tiобычно невысоки, и во вспомогательном контуре может быть использован П-регулятор с параметром настройки 5ц, найденным по приближенным формулам (табл. 1.2) для объекта с передаточной функциейWi(p). С помощью той же табли-

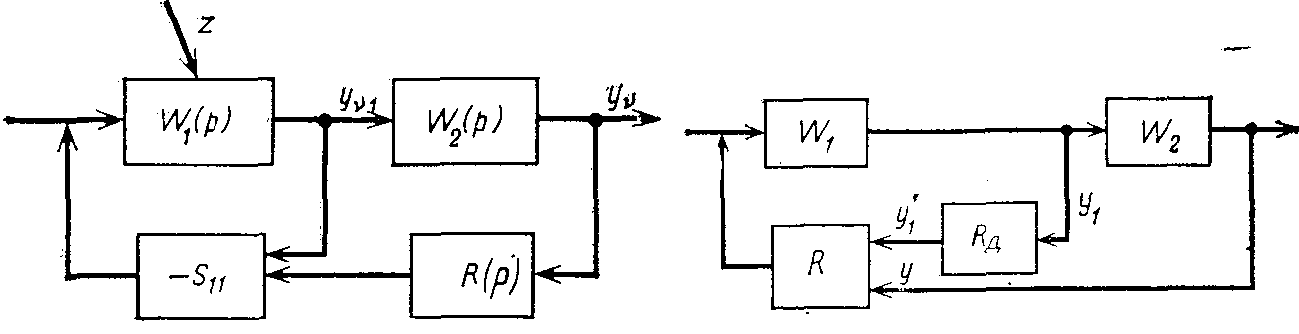
Рис. 1.53. Структура каскадной АСР

Рис. 1.54. Структура АСР с импульсом из промежуточной точки

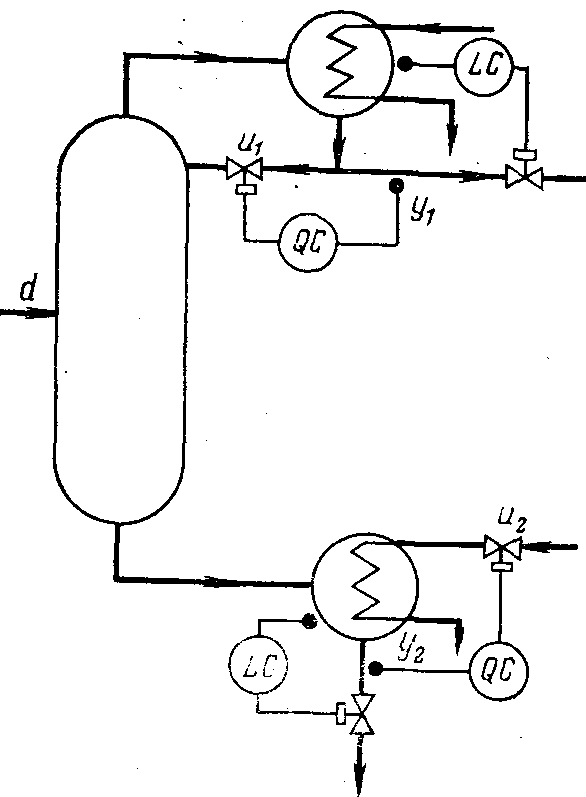
Рис. 1.55. Схема колонны ректификации

цы можно оценить о_у\ — среднеквадратичное отклонение промежуточной координаты.

Для вычисления среднеквад ратичного отклонения основной регулируемой переменной сле дует перейти к эквивалентной системе, в которой возмущающие воздействия z заменены возму щениемj/_vi, влияющим наy_v через передаточную функциюW₂(p) и имеющим дисперсиюо²_у\. Передаточная . функция эк вивалентного объектаW³ равна произведению передаточной

функции системы регулирования % 1 наW₂. Передаточная функция вспомогательного контура регулирования, содержащего П-регулятор, равна (см. табл. 1.2)

где через 5ц обозначен параметр настройки вспомогательного регулятора.

Аппроксимируя передаточную функцию эквивалентного объекта W_B(p)W2(p) апериодическим или интегрирующим звеном с запаздыванием, оцениваюто_у? для одноконтурной системы (по формулам табл. 1.2) с тем или иным типом основного регулятора и рассчитывают соответствующие значения показателя качества.

Для схемы с отбором импульса из промежуточной точки (рис. 1.54) параметры динамической связи, имеющей обычно вид реального дифференцирующего звена

стремятся выбрать так, чтобы эквивалентный объект, выходом которого является сумма у\' + у, в статическом режиме вел себя как объект с передаточной функциейWi(p)W₂{p), а при высоких частотах был близок к объекту с передаточной функциейWi{p)kclT_c- ЕслиW{(p) иW₂{p) аппроксимированы апериодическими звеньями с запаздыванием, то передаточная функция эквивалентного объекта приближенно равна

По ней и выбирают параметры регулятора (с использованием формул табл. 1.2) и рассчитывают а_у и соответствующее значение а.

Таблица 1.4. Предварительные сведения о динамике регулируемого объекта

.Примечание. Т, т —в мин.;у— ,в мольных долях;и_х — в кмоль/мин;w₂—в кг/мин;; г — в кг/мин.

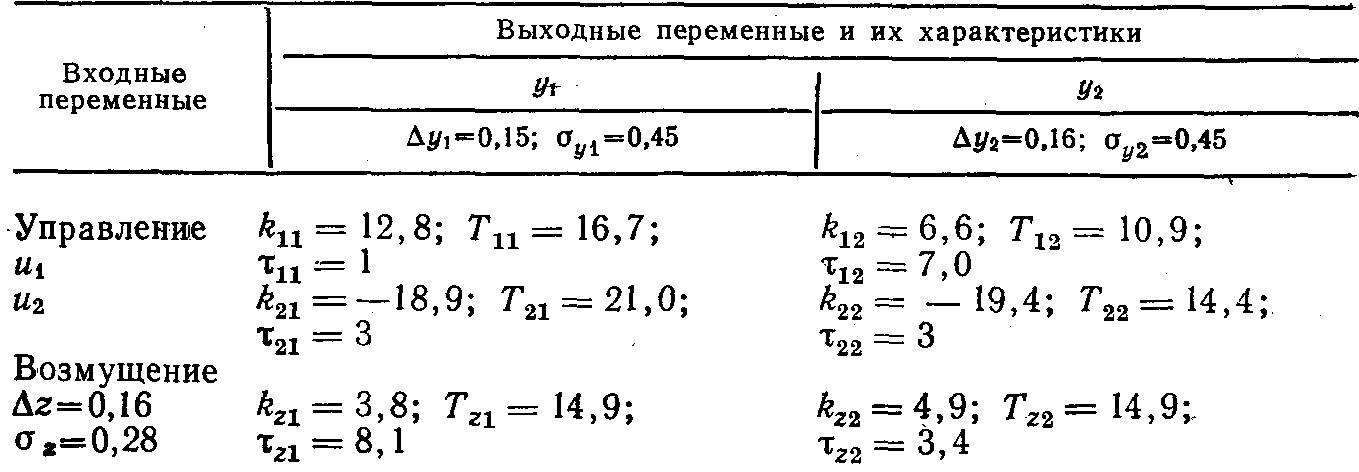
Пример. Проиллюстрируем последовательность применения изложенной методики на примере выбора системы регулирования для колонны ректификации смеси метанол — вода [43.] Схема колонны показана на рис. 1.55. Регулируемыми величинами являются мольные концентрации метанола в дистилляте и кубовой жидкостиi/iи 1/2, а также уровни жидкости в кубе и в дефлегматоре. Контуры регулирования уровней можно рассматривать в первом приближении независимо от концентраций. Будем полагать [43], что регулирование уровня в дефлегматоре осуществляется изменением расхода верхнего продукта, а в кубе — нижнего. Далее будем рассматривать, только регулирование состава. Управляющими воздействиями являются поток пара на входе в кипятильник м₂и поток флегмы, направляющийся в колонну «ь возмущением — поток разделяемой смеси.

Характеристики динамики колонны и требования к качеству регулирования можно свести в таблицу (табл. 1.4).

Определитель матрицы коэффициентов усиления

т. е. не равен нулю, и следовательно, объект статически управляем.

Максимальные отклонения У\ иу% в статическом режиме при отсутствии регуляторов равны

Ау₁= 3,8-0,16 = 0,61>0,15; Ду₂= 0,16-4,9 == 0,78 > 0,16.

Таким образом, установка регуляторов необходима.

Расчет настроек регуляторов по приближенным формулам табл. 1.2 дает следующие значения:

Для приведения возмущающих воздействий ко входу каждого из каналов регулирования нужно учесть, что возмущение, приведенное к выходу у_и складывается из влияния возмущенияг и воздействия второго контура регулирования по перекрестному каналу; аналогично — для возмущения контура регулированияу₂. Поэтому, строго говоря, нужно решить совместно систему уравнений

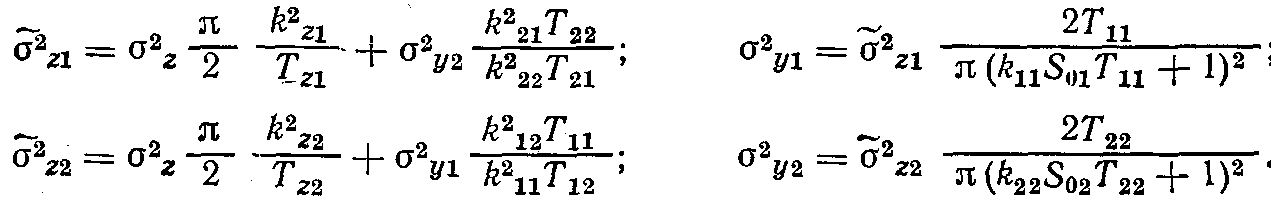
относительно а,,, и а^₂. В этих уравнениях а²_г/ — эквивалентные дисперсии возмущений, приведенных к выходу соответствующего канала регулирования. Однако при первом просчете можно упростить задачу, заменив в уравнениях для 0₂/ дисперсииа²_у\ иа²_у2 их максимально допустимыми значениями. Расчет при таком допущении приводит к следующим значениям оУ^р: а_г"-^р= = 0,16 и а_г^пр=0,13 при выборе и, для регулированияу\ ии₂— для регулированияу₂; oV^p=0,12, ст_г^пр=0,34 при выборещ для регулированияу₂ и и₂—для регулированияу_х (первыми указаны приведенные ко входу канала регулированияу\ среднеквадратичные значения возмущений).

Подсчитав оценки качества регулирования для П-регулятора, сведем их в таблицу вида

Из расчетов следует, что концентрацию кубового остатка </₂нельзя ре-тулировать с использованием П-регулятора ни по одному из каналов. При использовании для регулированияу% ПИ-регулятора по каналуи_х получим а>1, а по каналу «2—а=0,78. Таким образом, простейшей схемой регулирования колонны разделения смеси метанол — вода является схема с использованием П-регулятора (меняющего расход флегмы для поддержания концентрации дистиллята), ПИ-регулятора (меняющего расход пара в куб для поддержания концентрации в нем). При повышении требований к качеству регулирования эту схему придется усложнить.

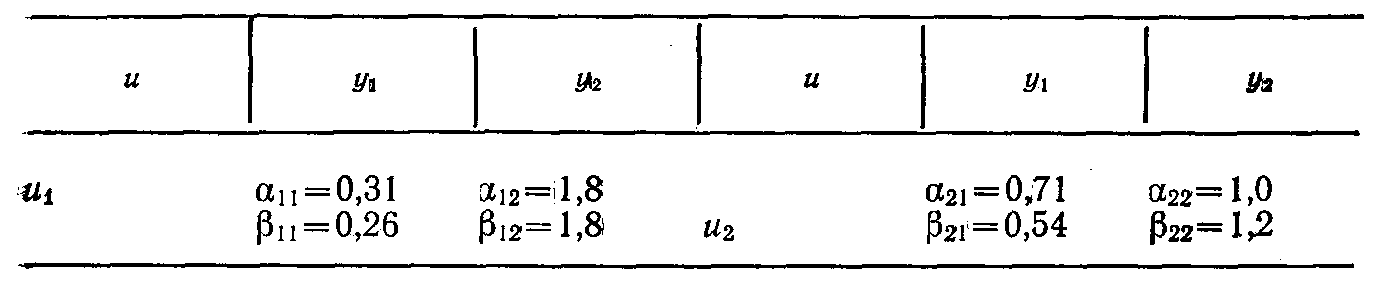
1.6. Оптимальная фильтрация и прогнозирование случайных процессов. Оптимальное оценивание состояния объекта

Один из способов формирования требуемого управляющего воздействия— синтез такой линейной системы (формирующего устройства), реакция которой на заданный входной сигнал совпадает с желаемым сигналом m(t) или мало от него отличается. Способ решения такой задачи позволяет понять существо методов оптимальной фильтрации и прогнозирования стационарных •случайных процессов.

Обозначим импульсную характеристику формирующего устройства w(t). Для физически реализуемой системы эта характеристика удовлетворяет требованию

(1.59)

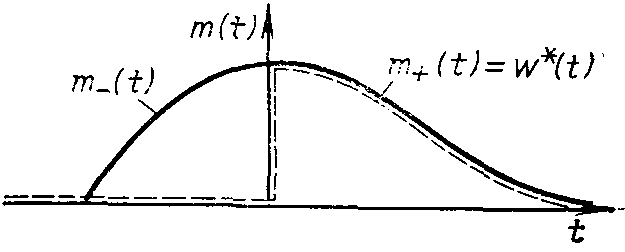
Рис. 1.56. Расщепление желаемого сигнала m(t) наm+(t) иm-{t)

Первоначально предположим, что сигналом на входе формирующего устройства является б-функция. Тогда его выходом является характеристика w(t); она должна минимизировать-квадр этичное отклонение

(1.60)

Если функция m(t) равна нулю приt<.0, то решение задачи очевидно:w*(t)=m(t).

Если m(t) отлична от нуля приt<C.O, то импульсная характеристика, минимизирующая (1.60), должна быть равнаm{t) лишь приf>0 и обращаться в нуль при отрицательных значенияхt. На рис. 1.56 показаны такая функцияm(t) и оптимальная импульсная характеристика.

Таким образом, во временной области решение задачи очевидно. Несколько сложнее решить ее, если условия заданы в частотной области. Например, задано преобразование па Фурье М(ш) функцииm(t) и требуется найти амплитудно-фазовую частотную характеристикуW(m) формирующего устройства. Для определенияW*{ia>) нужно представитьМ(т) в виде суммы двух слагаемых:

(1.61>

Первому слагаемому соответствует оригинал m+{t), равный-нулю при отрицательных значенияхt, а второму — при положительных. Разложение (1.61) называютрасщеплением. Равенствоw(t)=m+(t) в частотной области запишется следующим образом:

(1.62)

Если функция М(ш) дробно-рациональная, то разложение (1.61) можно выполнять, не переходя к оригиналам, а воспользовавшись тем, что для функцииf(t), равной нулю приt<C0 и стремящейся к нулю при /->-оо, преобразование ЛапласаF(p) имеет все полюсы в левой полуплоскости комплексного переменного. Наоборот, функция, равная нулю при />0, имеет преобразование Лапласа с полюсами в правой полуплоскости.

Пример. Пусть

Преобразование Лапласа получим из преобразования Фурье заменой toнар-

^М{р>- (p+i)(p_i) =7+T+"F^rT-

В первом из этих слагаемых полюс р°=—1,так что это М+, во втором полюс равен +1, этоAf_. КоэффициентыА иВ определим, приведя последнее равенство к общему знаменателю и учитывая, что числитель полученного выражения должен равняться р:

Ар + А + Вр — В = р.

Из условий равенства коэффициентов при одинаковых степенях р получим:А+В=\; А—В=0. Отсюда Л = В = 0,5. Таким образом

*Mto)=2(to+l)^=Г*('^Ю>-

Обобщим задачу синтеза формирующего устройства, предполагая, что на его вход подается сигнал g(t) и требуется так подобрать импульсную характеристикуw(t), чтобы выход устройстваy(t) минимально отличался от желаемого сигналаm{t).

Если g(t)=0 при ^<0, задача сводится к предыдущей, так как приt<ZQ y(t)=0; при ^>0 нужно сформироватьy(t) равнымm₊(t). В частотной области

7* (to) =G (to)W* (to) =М₊ (to),

откуда

W* (((о) =М+ (to)/G(гсо).

Если #(£) =5^0 при /^,<0, поступим следующим образом. Отбросим условие физической реализуемости и запишем в частотной области условие равенства желаемого сигнала и сигнала на выводе формирующего устройства:

G(to)W (to) =М (to). (1.63)

Преобразуем это равенство к такой форме, чтобы оригинал слагаемого, зависящего от W(ia>), обращался в нуль при /<0. Для этого представимG(ico) в виде

G(to) =G+(to)G-(to).

Здесь первому сомножителю соответствует оригинал, равный нулю при КО, второму — при />0. Такое представление называют факторизацией. Поделим обе части равенства (1.63) наС~(ш). Получим:

G+ (to)W ((со) =М ((co)/G- (to). (1.64)

Согласно условию физической реализуемости, оригинал функции W(ia>) и, следовательно, произведенияG+(i<B)W(ico), должен обращаться в нуль при ^<0; приt^O выборомW(i(a) можем добиться равенства функций времени, соответствующих левой и правой частям выражения (1.64). Таким образом, наи-

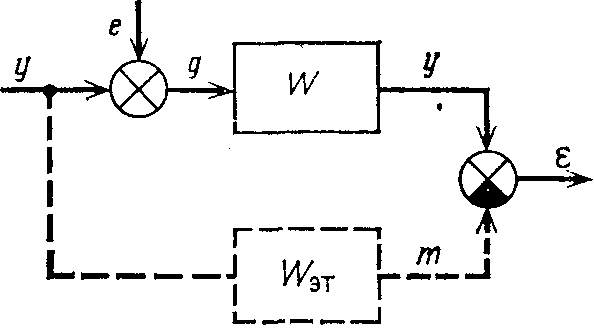
Рис. 1.57. Схема, иллюстрирующая постановку задачи оптимальной фильтрации

лучшему выбору соответствует условие

Индекс «плюс» в нижней части квадратной скобки соответствует расщеплению дроби MfG~ на два слагаемых:

Оригинал первого равен нулю при t<CQ, второго — приf>0. Окончательно получим:

Таким образом, учет требований физической реализуемости формирующего устройства осуществляют в частотной области с помощью двух операций —факторизации и расщепления. Факторизацию используют для того, чтобы множителем при W(i(u) оказалась функция, которой во временной области соответствует оригинал, равный нулю при t<0. Операция расщепления соответствует во временной области разбиению оригинала на два слагаемых, одно из которых определено для t^O, другое —для t<.0.

Оптимальная фильтрация и прогнозирование случайных процессов. Пусть на вход линейной системы (фильтра) подается случайный сигналg(t), равный сумме полезного сигналаy(t) и помехиe(t). Дляy(t) иe(t) известно, что это случайные стационарные процессы со спектральными плотностямиS_y((o) иS_e((a). Требуется найти такую характеристику фильтраW(m), чтобы сигналу (t) на его выходе минимально в среднеквадратичном смысле отличался от желаемого сигнала (рис. 1.57). В свою очередь, желаемый сигнал тем или иным способом связан с полезным сигналом. Если, например,m(t)=y(t), то задача фильтра заключается в выделении сигнала из его смеси с помехой. Еслиm(t)=dy/dt, фильтр реализует помехоустойчивое дифференцированиеy(t). Еслиm(t)=y(t+x), осуществляется помехоустойчивый прогноз полезного сигнала. В общем случае связь междуy(t) иm(t) удобно задать в частотной области в виде

При этом частотная характеристика оператора связи далеко не

всегда физически реализуема. Для задачи выделения полезного сигнала W_9r(ia) — l; для задачи дифференцирования №_Эт(ио) =«о; для задачи прогнозаW₃i(m) =e'^MT. Физически реализуема характеристика эталонного оператора только в первом из этих трех примеров.

Критерием оптимальности поставленной задачи является среднеквадратичная величина ошибки е между желаемым сигналом и сигналом у на выходе фильтра. Обозначая для краткости чертой операцию усреднения, запишем:

В частотной области среднеквадратичная ошибка запишется в форме

Здесь S_e(<»)—спектральная плотность ошибки, которая выражается через спектральную плотность сигналаg(t) на входе фильтра, его частотную характеристику и взаимную спектральную плотность входного и желаемого сигналов:

Условие минимума этого выражения по №(<ш) с учетом того, что ]W(i(o) \²=W(m)W(—ia), а производнаяdW(—ш)/ /dW(m) =—1, приводят к равенству

(1.65)

При этом требование физической реализуемости фильтра никак не учитывалось. Произведение S_g(a))W(m) равно, как известно, взаимной спектральной плотности сигналов на входе и выходе фильтраS_gy(m).

Таким образом, амплитудно-фазовую характеристику фильтра без учета физической реализуемости следует выбирать так, чтобы взаимная спектральная плотность сигнала на входе и выходе фильтра была равна взаимной спектральной плотности входного и желаемого сигналов. Для некоррелированных сигналаy(t) и помехиe(t) спектральная плотность входного сигнала

Взаимная спектральная плотность g(t) иm(t) может быть выражена через характеристику эталонного оператора ^этМ:

Таким образом, АФХ оптимального фильтра, найденная беа

учета физической реализуемости, имеет'вид:

(1.66)

Если оказывается, что найденная таким образом характеристика реализуема, она дает оптимальное решение. Однако знать эту характеристику полезно и тогда, когда она не реализуема, так как при подстановке ее в 5_е(со) вычисленное значение среднеквадратичной ошибки дает тот нижний предел, меньше которого эта ошибка заведомо быть не может.

Перейдем к учету условий физической реализуемости. Аналогично задаче синтеза формирующего устройства преобразуем равенство (1.66) так, чтобы зависящее от W слагаемое имело оригинал, равный нулю приi^<0. Для этого проведем факторизациюSg(co):

Оригинал первого сомножителя отличен от нуля при /^0, а второго — при ^<;0. В силу симметрии S_g(co) функцииS_g⁺ и 5_Й~ удовлетворяют равенству

Разделив обе части этого равенства на S_g~, получим:

(1.67)

Левая часть этого равенства для физически реализуемой функции W(m) имеет оригинал, равный нулю при /<0, а приf^tO выборомW можем сформировать нужную функцию. Наилучшему выборуW соответствует совпадение оригиналов от левой и правой частей равенства (1.67) приt^O. После расщепления правой части равенства (1.67).

где знак «плюс» соответствует функции, оригинал которой отличен от нуля лишь при t^Q, получим для выбораW условие

Отсюда

(1.68)

Пример. Решить задачу об оптимальном выделении сигнала у из смеси с помехойе, если спектральные платностиS_y иS_e имеют вид

а корреляция полезного сигнала и помехи отсутствует.

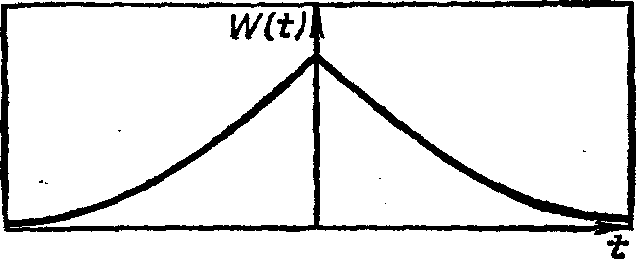
Рис. 1.58. Импульсная характеристика физически нереализуемого фильтра

Без учета физической реализуемости фильтра его частотная характеристика примет форму

Соответствующая импульсная характеристика показана на рис. 1.58. Чтобы учесть физическую реализуемость, проведем факторизацию S_g:

и расщепление S_gm/S_a-:

Для определения А и В имеем урав!

Откуда

Теперь получим

Оптимальным физически реализуемым фильтром оказалось апериодическое звено с оптимально найденными коэффициентом усиления и постоянной времени (экспоненциальный фильтр, см. разд. 3.3).

Обобщение задачи оптимальной фильтрации. Рассмотренная выше задача оптимальной фильтрации была обобщена в самых разных направлениях. Остановимся на одном из таких обобщений, связанным с тем, что ошибка системы для разных частот имеет различный вес. Этот фактор можно учесть, введя в критерий оптимальности весовую функцию, в результате чего он примет вид:

(1.69)

Чем больше весовая функция #(©) на некоторой частоте, тем меньше ордината спектральной плотности ошибки, соответствующая оптимальному решению. Примером критерия, имеюще-

го вид (1.69), служат обобщенные интегральные критерии, где наряду с дисперсией ошибки е учитывается дисперсия ее производных. Так, минимизация выражения

эквивалентна минимизации интеграла

Весовая функция Ц-^²©²на высоких частотах возрастает, поэтому спектр ошибки для оптимального фильтра окажется низкочастотным.

Полученную выше формулу для расчета АФХ оптимального фильтра нетрудно распространить на случай функционала (1.69). Для этого нужно записать условие стационарности функционала /я по W. Очевидно, это условие будет отличаться от равенства (1.65) только тем, что левая и правая его части будут содержать в качестве множителя функциюН_ш. Получим:

(1.70)

Для расчета оптимальной физически реализуемой АФХ фильтра проведем, как и выше, факторизацию S_g иН, после чего поделим левую и правую части равенства (1.70) на произведениеS_g~H~. Получим:

Для оптимального физически реализуемого фильтра оригиналы левой и правой частей этого условия должны совпадать при t^O. После расщепления правой части равенства придем к оптимальному решению в форме

(1.71)

Оптимальнее оценивание состояния объекта. В задаче оптимальной фильтрации предполагались известными спектральные плотности полезного сигнала и помехи, которые могут быть найдены посредством статистической обработки реализаций этих стационарных и эргодических процессов. При этом мы не предполагали известным механизм генерации этих сигналов. Между тем, если полезный сигнал представляет собой вектор-функцию у, характеризующую состояние технологического процесса, то приближенно известна его математическая модель; часть составляющих вектора состояния или некоторые зависящие от него переменные можно измерять и по результатам текущих измерений уточнять оценкуу; сигнал, а в некоторых случаях и помехи, нельзя считать стационарными процессами.

Рис. 1.59. Структура системы оценивания

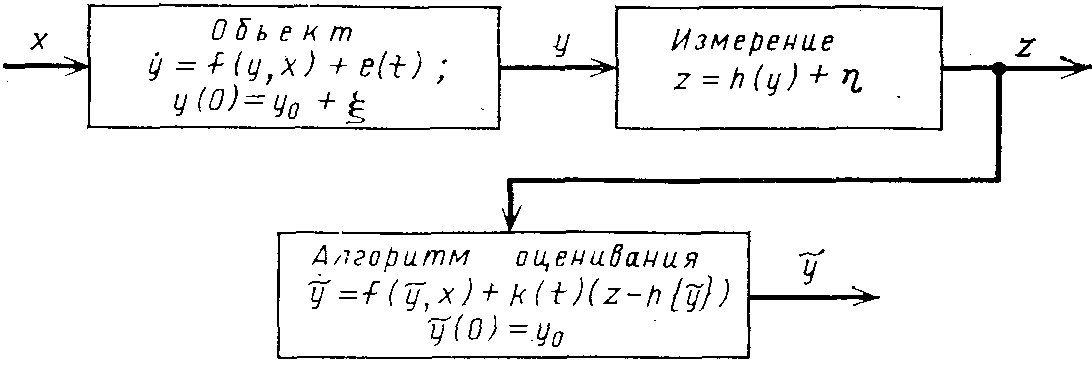
Расчет функции у (t) при таких предположениях называютоцениванием состояния; если же в моментt нужно рассчитать у(/+т), то имеем задачуоценивания с прогнозом состояния. Схема, иллюстрирующая постановку задачи оценивания, приведена на рис. 1.59. Предполагаются известными модель объекта: статистические характеристики сигналове, | иг\, характеризующие ошибки и случайные возмущения в модели, ошибки при измерении входных воздействий и при измерении переменных состояния соответственно; функцияz (t) и вектор Потребуется оценить вектору в моментt или(t+x). Основы теории оценивания развиты в работах Калмана и Бьюси [23].

Для систем регулирования модель объекта можно линеаризовать. Поэтому рассмотрим синтез алгоритма оценивания для линейных систем. Модель системы в векторно-матричной форме записи имеет вид (1.72), а модель измерений — вид (1.73):

(1.73)

Начальные условия уравнения (1.72) случайны:

(1.74)

В уравнениях (1.72) — (1.74) y(t)—n-мерный вектор состояния;z(t) — /-мерный вектор измеряемых выходов;e(t)—«-мерный вектор случайных возмущений;t\(t)—/-мерный вектор случайных ошибок измерений;g— случайная составляющая начальных условий;А — квадратная матрица(пУ<.п); С — прямоугольная матрица(1Хп).

Требуется по наблюдениям за процессом z(t) найти такую оценку состояния процессаy(t), при которой достигает минимума критерий

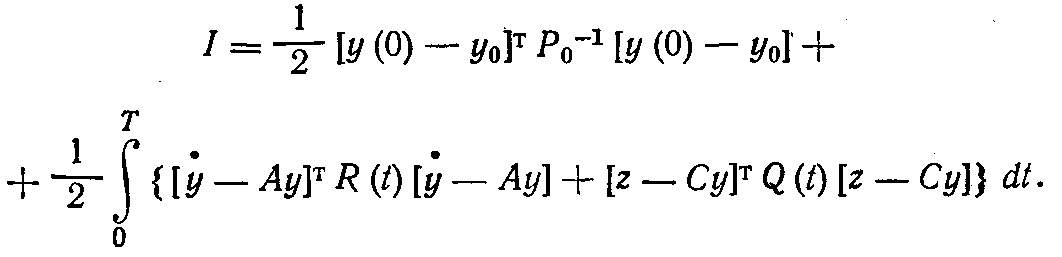(1.75)

Здесь Т — интервал, в течение которого проводят наблюдения. Первое слагаемое в (1.75) представляет собой квадратичную

форму разности между начальным значением оценки г/(0) и начальным состоянием процесса г/о- Подобные же квадратичные формы, оценивающие погрешность модели и измерений, содержатся в подынтегральном выражении функционала. Матрицы Лг¹,i? иQопределяют весовые коэффициенты, оценивающие важность той или иной составляющей ошибки. Пустьe(t), т)(0—случайные процессы типа белого шума, не коррелированные друг с другом и со случайным вектором |, а их средние значения равны нулю. В качестве матрицыР₀ берут матрицу ковариаций случайной помехи £ оценки начального состояния:

Здесь черта, как и ранее, соответствует операции взятия математического ожидания. В этом частном случае, когда составляющие вектора £ не коррелированы друг с другом, матрица Ро диагональная, и ее элементами являются дисперсии отдельных составляющих вектора |. Аналогично матрицы весовых коэффициентовR(t) иQ(t) обратны матрицам ковариаций процессовe(t) иx\(t):

(1.76)

По диагоналям этих матриц стоят корреляционные функции отдельных составляющих процессов e(t) иr\(t),a на остальных местах — взаимнокорреляционные функции двух разных составляющих этих процессов. Элементы ковариационных матриц случайных ошибок отражают неопределенность наших знаний. Чем больше эта неопределенность, тем с меньшим весом входит соответствующее слагаемое в критерийI.

Для решения задачи о минимуме / удобно ввести новую переменную

(1.77)

и переписать критерий / в форме

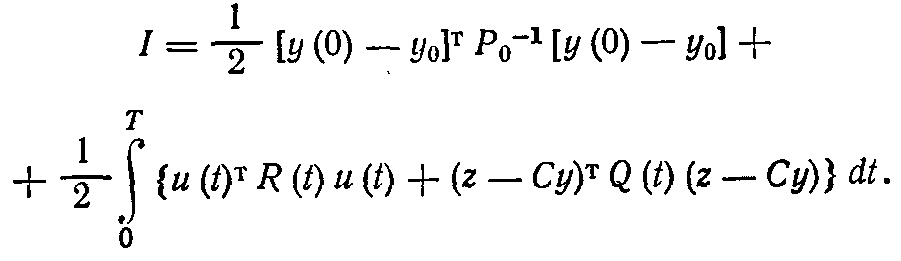(1.78)

При этом необходимо учесть связь (1.77) между у я и:

(1.79)

Функцию z(t) можно наблюдать; минимум ищется поу(0) иг/. Поставленная задача выпукла, поэтому ее решение существует и является единственным. В соответствии с процедурой принци-

па максимума [40] запишем для задачи (1.78), (1.79) функцию Гамильтона

и потребуем ее стационарности по и (для выпуклой дифференцируемой функции максимум достигается в точке стационарности) :

(1.80)

Уравнения для сопряженных переменных

или

(1.81)

Краевые условия для уравнения (1.81)—нулевые: г|з(7')=0. Начальное значение i|)(0) определяется [53] в виде

(1.82)

откуда

(1.83)

Подставляя (1.80) в уравнение (1.79), получим:

(1.84)

Таким образом, для вычисления оптимальной оценки y*(t) состояния процесса необходимо решить совместно уравнения (1.81) и (1.84), причем для уравнения (1.81) заданы условия в конце интервала наблюдения приt = T, а для уравнения (1.84) начальные условия определены через г|)(0). Так как граничные условия дляу и г|) заданы на разных концах интервала наблюдения, то одно из уравнений нужно решать в прямом времени, а другое — в обратном. Однако посколькуу входит в правую часть уравнений (1.81), а ^ — в правую часть уравнений (1.84), подобная процедура затруднена. Чтобы «развязать» систему (1.81), (1.84), удобно перейти к вспомогательным переменнымЪ и ввести вспомогательную матрицуР, так что

(1.85)

Подставляя это выражение в (1.84), получим:

(1.86)

С учетом (1.81) имеем:

(1.87)

Подберем теперь вспомогательную матрицу Р так, чтобы в (1.87) сумма слагаемых, содержащихty, обратилась в нуль. Эта сумма равна

Условие ее равенства нулю приводит к дифференциальному уравнению для матрицы Р:

(1.88>

Если матрица Р удовлетворяет уравнению (1.88), то из равенства (1.87) вытекает уравнение для расчета вектораb(t):

(1.89)

Начальные условия для уравнений (1.88), (1.89) следует из начальных условий (1.82) для ib. Действительно, требование

окажется выполненным, если

(1.90)

Уравнения (1.88) и (1.89) не содержат в правых частях никаких других переменных, кроме Р, Ь и наблюдаемого вектораг. Они могут быть проинтегрированы в прямом времеви от £=0 доt=T. Это позволяет выразитьty(t) черезy(t) в соответствии с (1.85), найтиy{T)=b{t) и переписать уравнение (1.86)ввиде

Решение этого уравнения в обратном времени определит искомую оценку у (t).

Однако полученная оценка может быть найдена лишь для тех моментов t, которые лежат внутри интервала наблюдения (О,Т). Часто требуется оценить вектор состояния в моментТ или даже прогнозировать его значение нах вперед. В первом случае оценка вытекает непосредственно из условия яр (7") = О, т. е.y(t) (гдеt — текущий момент времени, совпадающий с концом интервала наблюдения) получается из решения уравнения (1.89.) заменой в немb(t) наy(t):

(1.91)

Здесь матрица Р определяется уравнением (1.88).

Прогнозирующую оценку у (t+x) получают из уравнения (1.91) интегрированием его до моментаt+x. При этом начиная с моментаt доt+x матрицуQ(t), определяющую веса погрешностей измерения, полагают равной нулю (измерения отсутствуют, их неопределенность сколь угодно велика), т. е. на участке

:Рис. 1.60. Изменение во времени элементов матрицы Р(а), истинных составляющих векторау и составляющих его оценкиу (б)

от / до t+x уравнение (1.91) упрощается и принимает вид:у= =Ау. Аналогично на интервале{t, t+x) упрощается уравнение (1.88) для подсчета элементов матрицыР.

Пример {43]. Процесс в проточном химическом реакторе с непрерывным

перемешиванием характеризуется системой дифференциальных уравнений

Измеряется с ошибкой г\ только концентрацияу г:

Случайные возмущения £/, обусловленные неконтролируемыми изменениями расходов, температур, состава сырья и т. п., имеют среднее значение, равное нулю, являются белыми шумами (т. е. их автокорреляционные функции представляют собой б-функции). Матрица ковариаций их известна:

где pti=\i²{t); pu=\iJ[t)\j{t), т. е. диагональные элементы представляют собой дисперсии случайных возмущений,api2=P2i— коэффициенты их взаимной корреляции. Процессы%i(t) не обязательно стационарны, и матрицаR~^l может зависеть отt.

Аналогичные предположения сделаем о случайной функции r\(t) и векторе 1о:

Здесь

Уравнение для оценки вектора y(t) по результатам текущих измерений на интервале (0,0 примет вид уравнения (1.89), в которомp(t)=b(t):

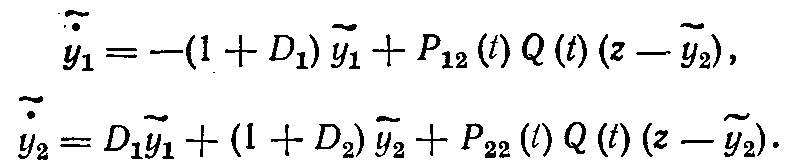
Элементы матрицы Р вычисляются согласно уравнению (1.88):

Начальные условия для этой системы определены матрицей Ро. Решение уравнений (1.92) не зависит от текущих измеренийz(t), поэтому к моментуt в уравнениях для оценкиу матрицаР известна; при получении очередного значенияz эти уравнения интегрируются в реальном времени.

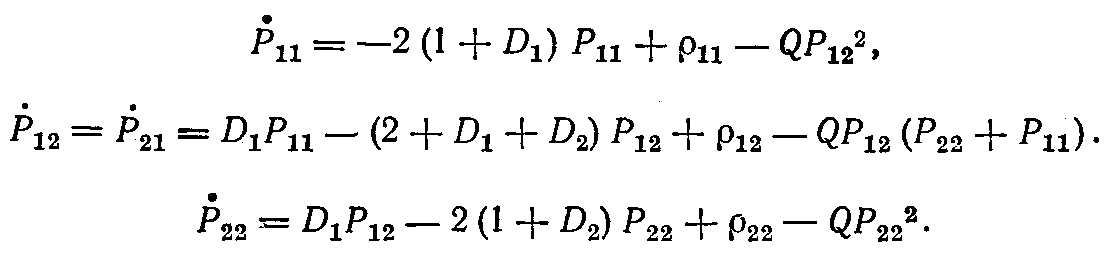
На рис. 1.60 показаны изменения во времени элементов матрицы Р, а также оценки вектора концентрацийу в системе для следующих исходных, данных:

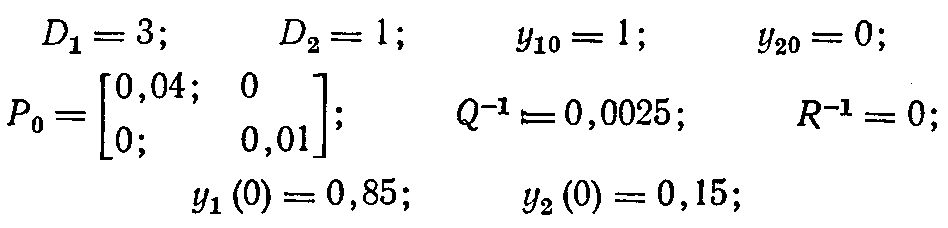
дисперсия погрешностей измерения Q~' = 0,05.