4.3. Учет и компенсация динамических связей между измеряемыми величинами

В формулу (4.3) для расчета ТЭП в качестве переменных Х{, как правило, входят расходы материальных и энергетических потоков, измеряемые в разных точках объекта управления.

Например, расходный коэффициент по аммиаку, являющий­ся одним из основных ТЭП работы агрегата по производ­ству разбавленной азотной кислоты, равен отношению расхода аммиака, измеряемого на входе агрегата, к расходу продук­ционной кислоты, измеряемому на его выходе.

Для получения правильного результата при расчете опера­тивных ТЭП по текущим значениям измеряемых величин эти значения должны быть согласованы между собой во времени с учетом динамических характеристик объекта управления. Обычно, если хотя бы один из параметров, входящих в расчет­ную формулу ТЭП, измеряется на выходе объекта, то значе­ния всех остальных параметров также «приводятся» к его вы­ходу.

Рассмотрим простейший случай, когда в формулу (4.3) для расчета оперативного ТЭП входят величины х и у, измеряемые соответственно на входе и выходе линейного объекта 1 (рис. 4.3). Текущие значения величин х(t) и у(t) связаны уравнением

. (4.23)

где - импульсная переходная функция (ИПФ) объекта.

С учетом условия физической реализуемости ИПФ при<0 и конечной «памяти» реальных объектов

Рис. 4.3. Модель расчета опера­тивного ТЭПи=Цх, у):

1— объект контроля; 2—динамическое звено, моделирующее приведение сиг-вала х(1) к выходу объекта; 3 — ста­тическое звено, моделирующее вычисле-иие ТЭП

Рис. 4.4. График к расчету приведен­ного значения измеряемой на входе величины к выходу объекта по фор­муле (4.26)

при _max из (4.23) получим:

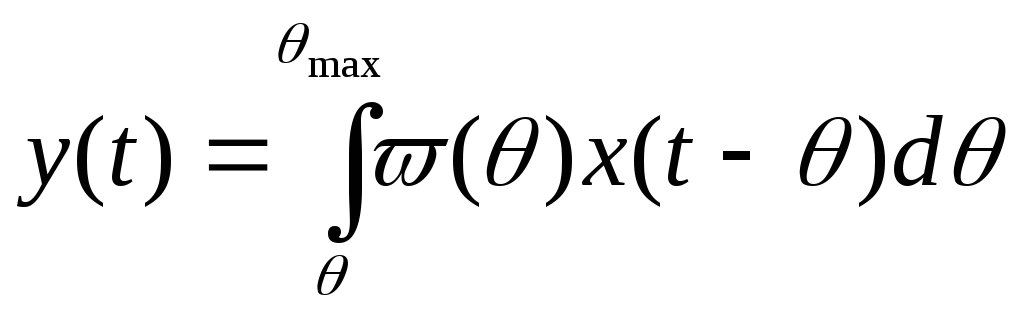(4.24)

Текущее значение величины х(t), «приведенное» к выходу объекта (t), получают делением правой части (4.24) на коэф­фициент усиления k₁ объекта:

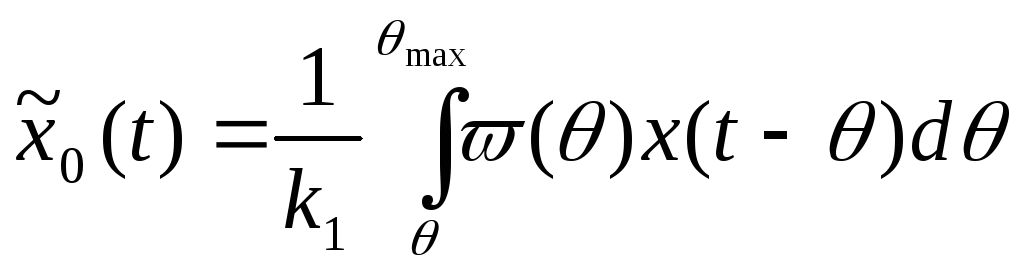. (4.25)

Вводя в рассмотрение нормированную ИПФ , получают окончательно:

. (4.26)

Формула (4.26) дает алгоритм приведения текущего значе­ния измеряемой на входе величины к выходу объекта. Он сво­дится к вычислению интеграла свертки нормированной ИПФ объекта и функциих(t), взятой на отрезке времени от текущего момента t_j, до t_j -_max (рис. 4.4). Расчет можно вы­полнять любым численным методом интегрирования, например методом прямоугольников. Для этого необходимо постоянно хранить в памяти УВМ т ординат нормированной ИПФ, кван­тованной по времени с тем же периодом t₀, с которым кванто­вана измеряемая функция х(t)~.

, (4.27)

где Int() —функция «целая часть от».

Кроме того, для расчета требуется т ординат (отсчетов) функ­ции х(t), начиная с полученной в текущий момент t_j=jt₀ и до момента t_j-m-1=(j-m-1) включительно. Расчет выполняют по формуле

. (4.28)

Алгоритм (4.26) обеспечивает максимальную точность при­ведения к выходу объекта функции х(t), измеряемой на его входе, однако он относительно сложен и трудоемок для реализации, особенно на микро-ЭВМ. Поэтому на практике широкое распространение получили несколько упрощенных алгоритмов, рассмотренных ниже.

Обозначим через (t) текущее значение функции х(t), при­веденное к выходу объекта по k-му упрощенному алгоритму. Тогда текущая методическая погрешность k-го алгоритма равна:

. (4.29)

Из сопоставления (4.24) и (4.25) следует*, что

. (4.30)

поэтому

. (4.31)

Если (t) является несмещенной оценкой (t), то с учетом (4.30) можно записать:

, (4.32)

где М{z(t)}—символ операции определения математического ожидания функцииz(t);т_x ит_y —математические ожидания функциих(t)иу(t).

С учетом (4.32) выражение (4.31) можно преобразовать сле­дующим образом:

, (4.33)

где ицентрированные функции (t)иу(t).

Дисперсия D_k методической погрешности k-го приближен­ного алгоритма приведения равна:

Из (4.30) следует, что D_y=k²₁D_x. Поэтому окончательно полу­чим

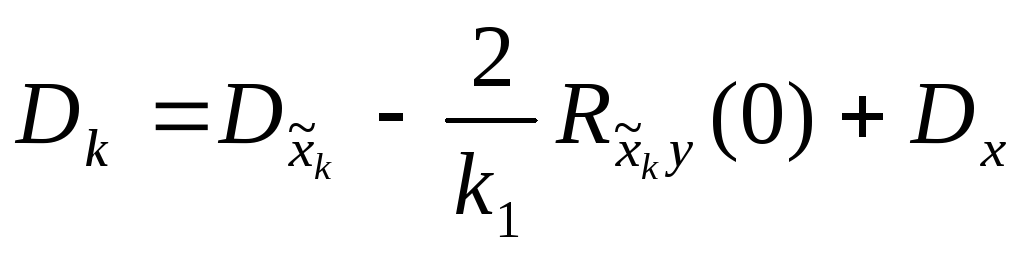, (4.34)

где иD_xдисперсия функции(t)их(t); ()—взаимнокорреляционная функция процессов(t)иy(t).

Первым из приближенных алгоритмов приведения рассмотрим алгоритм 1, по которому приведенное значение функции рассчитывают по формуле

, (4.35)

где a,bи— параметры алгоритма.

Для обеспечения несмещенности оценки должно вы­полняться условие

M { }=m_x. (4.36)

Найдем математическое ожидание для правой части (4.35):

М{}=am_x+b.

Подставив полученное выражение в условие (4.36), определим значение параметра b, обеспечивающее несмещенность оценки :

b=m_x(1-a). (4.37)

Чтобы определить оптимальные значения параметров а и , необходимо рассчитать дисперсию методической погрешности алгоритма (4.35) по формуле (4.34). С этой целью требуется найти для данного алгоритма дисперсию и значение взаимнокорреляционной функции(0). Согласно определе­нию, можно записать:

После подстановки в эти выражения значения функции(t) из формулы (4.35) с учетом (4.37) получим:

Подстановка полученных выражений в (4.34) дает:

. (4.38)

Оптимальные значения параметров a и  алгоритма приве­дения (4.35) получают из условий минимума дисперсии D₁. Для , оптимальным, очевидно, является значение, доставляю­щее абсолютный максимум функции R_yx():

^*=argmaxR_yx(). (4.39)

Оптимальное значение параметра а находят из необходимого условия минимума функции D₁ по этому параметру, т. е. из условия D₁/a=0. В результате получают

a^*=R_yx(^*)/(k₁D_x). (4.40)

Минимальное значение дисперсии методической погрешности приведения по алгоритму (4.35), получаемое после подстанов­ки в формулу (4.38) оптимальных значений параметров ^* из (4.39) и а* из (4.40), равно:

. (4.41)

Другие приближенные алгоритмы приведения представляют собой частные случаи алгоритма (4.35).

Алгоритм 2 отличается от (4.35) тем, что в нем временной сдвиг =0, т. е.

=ах(t)+b. (4.42)

В этом случае значение параметра b, обеспечивающее несме­щенность оценки , подчиняется условию (4.37). Оптималь­ное значение второго параметра алгоритма определяют по формуле (4.40), в которой *=0, так что

a^*=R_yx(0)/(k₁D_x). (4.43)

Минимальная дисперсия методической погрешности приведе­ния в этом случае возрастает по сравнению с D^*₁ на вели­чину

. (4.44)

Алгоритм 3 отличается от (4.35) тем, что а=1 и в силу (5.37) b=0. Поэтому

. (4.45)

Оптимальное значение единственного параметра этого алго­ритма определяют по формуле (4.39). Минимальная дисперсия методической погрешности этого алгоритма равна:

. (4.46)

Алгоритм 4 отождествляет приведенное к выходу объекта значение параметра х с измеренным его значением:

=х(t). (4.47)

Дисперсия погрешности в этом случае максимальна и равна:

. (4.48)

Оценим точность различных алгоритмов приведения на примере про­стейшего объекта — апериодического звена с ИПФ

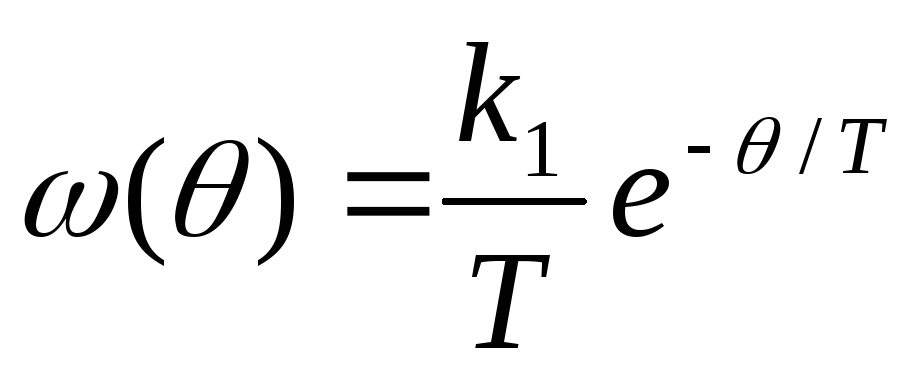, (4.49)

на входе которого измеряется функция х(t),представляющая собой стацио­нарный случайный процесс с автокорреляционной функцией

. (4.50)

Взаимнокорреляционную функцию [50] рассчитываем по формуле

Подставляя в нее выражения (4.49) и (4.50), выполняя интегри­рование и группируя члены, получим:

Координату точки максимума этой функции найдем из условия

Выполняя дифференцирование и промежуточные преобразования, получим

при T>1.

Примем для определенности =1 ч иT=2 ч. Тогда

*= 0,81 ч;;.

Согласно (4.48), (4.46) и (4.41), имеем:

; ;

Таким образом, в данном случае дисперсия методической погрешности -при использовании алгоритма 3уменьшается по сравнению с полученной по алгоритму4на 16%, а при использовании алгоритма1она уменьшается еще в два раза. Следовательно, для приведения параметров к выходу объекта наиболее целесообразно использование алгоритма1.