5. Имитационное моделирование. Принципы построения моделирующих алгоритмов.

3 ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

3.1 ПРОЦЕДУРА ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ Способ имитационного моделирования заключается в создании логико-аналитической (математической) модели системы и внешних воздействий, в имитации функционирования системы, т.е. в определении временных изменений состояния системы под влиянием внешних воздействий, и в получении выборок значений выходных параметров, по которым определяются их основные вероятностные характеристики. При исследовании детерминированных систем необходимость в последнем отпадает.

Научно построенная имитационная модель не только адекватна словесному (содержательному) представлению реальной системы, но и обладает рядом преимуществ. К примеру, такая модель в процессе своего "жизненного" цикла в рамках модельного времени способна "развиваться", т. е. видоизменяться, как в целом, так и во взаимосвязях элементов ее составляющих. В этом смысле имитационная модель в определенной степени способна отобразить не только специфическую, но и органическую сущность системы.

Внедрение информационных технологий и адекватных им методов хранения и обработки информации, отображающей окружающий мир делает насущным движение исследователей систем в направлении использования современных методов имитационного моделирования. Имитационные модели позволяют динамически моделировать различные сценарии развития событий и прогнозировать результат тех, либо иных действий.

Модель системы на уровне структуры представляет собой совокупность моделей элементов и их функциональные взаимосвязи.

Модель элемента - это набор правил (алгоритмов) поведения устройства по отношению к входным воздействиям (заявкам) и правил изменения состояний элемента. При моделировании на системном уровне элемент отражает функциональное устройство на том или ином уровне детализации.

В частности, устройство может быть в работоспособном состоянии и в состоянии отказа. К правилам поведения устройства относятся правила выбора заявок из очереди, реакция устройства на поступление заявки, реакция устройства на возникновение отказа в процессе обслуживания заявки и некоторые другие.

Функциональные взаимосвязи устройств определяют возможные пути продвижения заявок по системе от входных устройств к выходным. Они формируют структуру системы.

Модель внешних воздействий - это правила определения моментов поступления входных сигналов (заявок) в систему, маршрута заявок в системе по каждому из потоков в соответствии с алгоритмами обработки, приоритетов обслуживания, трудоемкости обслуживания, допустимого времени пребывания заявок в системе.

В процессе имитации функционирования системы измеряют те выход­ные характеристики, которые интересуют исследователя. При изучении стохастических систем измерения производятся многократно, чтобы с достаточной точностью определить вероятностные характеристики. Это такие характеристики системы как время ожидания заявок в очереди, число заявок в системе, длина очередей к устройствам, требуемая емкость памяти. Имитационное моделирование дает возможность учесть надежностные характеристики ВС: моменты возникновения отказов устройств в период моделирования и моменты их восстановления (по известным временам наработки на отказ и восстановления всех входящих в систему устройств).

3.1.1. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ФАКТОРОВ

Имитационная модель позволяет исследовать поведение различных систем с учетом влияния случайных факторов. Эти факторы в зависимости от их природы могут быть отражены в модели как случайные события, случайные величины (дискретные или непрерывные), или как случайные функции (процессы).

Например, если с помощью создаваемой имитационной модели предполагается исследовать надежность вычислительной системы, то возникновение отказа будет представлено в модели как случайное событие. Если же модель предназначена для оценки временных параметров процесса обслуживания клиентов, то интервал времени до появления очередного клиента удобнее всего описать как. случайную величину, распределенную по некоторому закону.

В основе всех методов и приемов моделирования случайных факторов лежит использование случайных чисел, имеющих равномерное распределение на интервале [0; 1].

"Истинно" случайные числа формируются с помощью аналого-цифровых преобразователей на основе сигналов физических генераторов, использующих естественные источники случайных шумов (радиоактивный распад, шумы электронных и полупроводниковых устройств и т.п.).

Случайные числа, генерируемые аппаратно или программно на ЭВМ, называются псевдослучайными. Однако их статистические свойства совпадают со статистическими свойствами "истинно" случайных чисел. В состав практически всех современных систем программирования входят специальные функции генерации случайных чисел, которые обычно называют датчиками, случайных чисел .

Наиболее простой метод программной генерации случайных чисел использует рекуррентное соотношение:

где a_i, a_i-1, — очередное и предыдущее случайные числа соответственно;

А, С—константы;

М — достаточно большое целое положительное число (чем больше М, длиннее неповторяемая последовательность).

Достоинство метода заключается в том, что при одних и тех же значе­ниях входящих в выражение (3.1) величин можно полностью воспроизвести эксперимент.

Практика показывает, что результаты имитационного моделирования существенно зависят от качества используемых последовательностей псевдослучайных чисел.

Основные анализируемые характеристики генерируемых датчиком последовательностей - это равномерность, стохастичность (случайность),независимость.

Моделирование случайных событий. Для моделирования случайного события А, вероятность которого равна Рс, достаточно сформировать одно число r, равномерно распределенное на интервале [0,1].

При попадании r в интервал [0, Рс] считают, что событие А наступило, в противном случае — не наступило, т. е.:

Для моделирования полной группы N несовместных событий A={А1, А2,..., AN} с вероятностями соответственно P1, P2,..., PN также достаточно одного значения r. Событие А_i, из группы А считается наступившим, если выполняется условие

Если группа событий А не полна, то вводят фиктивное событие А_N+1 с вероятностью Р_N+1, такой, что

т. е. дополняют группу А до полной.

После этого генерируют число r и проверяют условие (3.2). При А_N+1 считают, что ни одно событие из исходной группы А не наступило.

Моделирование дискретных случайных величин. Наиболее часто используются два метода:

• метод последовательных сравнений;

• метод интерпретации.

Метод последовательных сравнений. Число r последовательно сравнивают со значением суммы

Р1+Р2+...,

где Р1 — вероятность наименьшего значения случайной величины У,

Р2 — вероятность второго по величине значения. При первом выполнении условия

проверка прекращается и дискретная случайная величина Y считается принявшей значение у_i.

Процесс можно ускорить, применяя методы оптимизации перебора: ди­хотомии, ранжирования Р и т. д.

Величины P_i рассчитывают по функциям распределения вероятности, соответствующим моделируемому закону.

Метод интерпретации основан на физической трактовке моделируемого закона распределения. Например, биномиальное распределение описывает число успехов в n независимых испытаниях с вероятностью успеха в каждом испытании Р и вероятностью неудачи Q = 1 - Р.

При моделировании этого распределения с помощью метода интерпре­тации выбирают п независимых случайных чисел, равномерно распределенных на интервале [0,1], и подсчитывают количество тех из них, которые меньше Р. Это число и является моделируемой случайной величины.

Моделирование непрерывных случайных величин. При моделировании могут используются три метода:

• • метод нелинейных преобразований;

• • метод композиций;

• табличный метод.

Первые два метода требуют от разработчика модели весьма серьезной математической подготовки. Третий метод, условно названный "табличным", основан на замене закона распределения непрерывной специальным расчетным соотношением, которое позволяет вычислять значение по значению случайного числа, равномерно распределенного на интервале [0,1]. Такие соотношения получены практически для всех наиболее распространенных видов распределений и приведены в справочной литературе. В качестве примера ниже даны расчетные соотношения для двух законов распределения — показательного

(3.3) где λ — параметр показательного распределения, r — равномерно распределенное случайное число, и нормального

(3.4) т, s - параметры нормального закона распределения, r_i, - равномерно распределенное случайное число. В одной и той же имитационной модели могут фигурировать различные случайные факторы, одни могут быть представлены как случайные события, другие - как случайные величины; более того, если моделируется поведение достаточно сложной системы, то ее функционирование может быть связано с возникновением нескольких типов событий и учетом большого числа случайных величин, распределенных по различным законам. Если же моделирование всех случайных факторов основано на использовании одного датчика, генерирующего одну "общую" последовательность случайных чисел, то с математической точки зрения их нельзя считать независимыми. В связи с этим для моделирования каждого случайной фактора стараются использовать отдельный генератор, или, по крайней мере, обеспечивать создание новой последовательности случайных чисел. Во многих специализированных языках и пакетах моделирования такая возможность предусмотрена.

3.2 ПРИНЦИПЫ ПОСТРОЕНИЯ МОДЕЛИРУЮЩИХ АЛГОРИТМОВ

Имитационный эксперимент представляет собой наблюдение за поведением системы в течение некоторого промежутка времени. В практике существует больше таких задач, в которых оценка эффективности моделируемой системы напрямую связана с временными характеристиками ее функционирования. К ним относятся - задачи по оценке производительности, некоторые задачи по оценке надежности, качества распределения ресурсов, а также все задачи, связанные с исследованием эффективности процессов обслуживания. Характерной особенностью большинства практических задач является то, что скорость протекания рассматриваемых в них процессов значительно ниже скорости реализации модельного эксперимента.

С другой стороны, даже те имитационные эксперименты, в которых временные параметры работы системы не учитываются, требуют для своей реализации определенных затрат времени работы компьютера.

В связи с этим при разработке практически любой имитационной модели и планировании проведения модельных экспериментов необходимо соотносить между собой три представления времени:

• реальное время, в котором происходит функционирование имитируемой системы;

• модельное (или, как его еще называют, системное) время, в масштабе которого организуется работа модели;

• машинное время, отражающее затраты времени ЭВМ на проведение имитации.

Функционирование модели М должно протекать в искусственном (не в реальном и не в машинном) времени, обеспечивая появление событий в требуемом логикой работы исследуемой системы порядке и с надлежащими временными интервалами между ними. Нужно учитывать, что элементы реальной системы S могут функционировать одновременно, а компоненты машинной модели М - последовательно. Для сохранения адекватности причинно-следственных временных связей для одновременно возникших событий, необходимо создать "механизм" задания времени для синхронизации действий элементов модели системы.

С помощью механизма модельного времени решаются следующие задачи:

1. отображается переход моделируемой системы из одного состояния в другое;

2. производится синхронизация работы компонент модели;

3. изменяется масштаб времени "жизни" (функционирования) исследуемой системы;

4. производится управление ходом модельного эксперимента.

1. моделируется квазипараллельная реализация событий в модели;

Приставка "квази" отражает последовательный характер обработки

событий (процессов) в модели, которые в реальной системе возникают и протекают одновременно.

Известны два подхода к заданию времени: с помощью постоянных и переменных интервалов времени, которым соответствуют два принципа реализации моделирующих алгоритмов, т. е. "принцип ∆t" и "принцип δz" (принцип особых состояний) и проиллюстрированы на рис 3.1.

Выбор метода реализации механизма модельного времени зависит от назначения модели, ее сложности, характера исследуемых процессов, требуемой точности результатов и т. д.

Рис. 3.1. Принципы реализации моделирующих алгоритмов

Под действием событий Si, имеющих место в системе S изменяются состояния z_i. модели М.

3.2.1. МЕТОД ПОСТОЯННОГО ШАГА

В модели, построенной по "принципу ∆t" , моменты системного време­ни будут последовательно принимать значения tl=∆t , t2=2∆t , t3=3∆t, t4=4∆t. Эти моменты системного времени tj(∆t) никак не связаны с моментами появления событий Si, которые имитируются в модели системы. Системное время при этом получает постоянное приращение, выбираемое и задаваемое перед началом имитационного эксперимента.

При использовании метода постоянного шага отсчет системного времени ведется через фиксированные, выбранные исследователем интервалы времени. События в модели считаются наступившими в момент окончания этого интервала. Погрешность в измерении временных характеристик системы в этом случае зависит от величины шага моделирования ∆t . Метод постоянного шага предпочтительнее, если:

• события появляются регулярно, их распределение во времени достаточно равномерно;

• число событий велико и моменты их появления близки;

•невозможно заранее определить моменты появления событий. Данный метод управления модельным временем достаточно просто

реализовать в том случае, когда условия появления событий всех типов в модели можно представить как функцию времени.

В общем виде алгоритм моделирования с постоянным шагом представлен на рис. 3.2. (t_M—текущее значение модельного времени, Т_м- интервал моделирования).

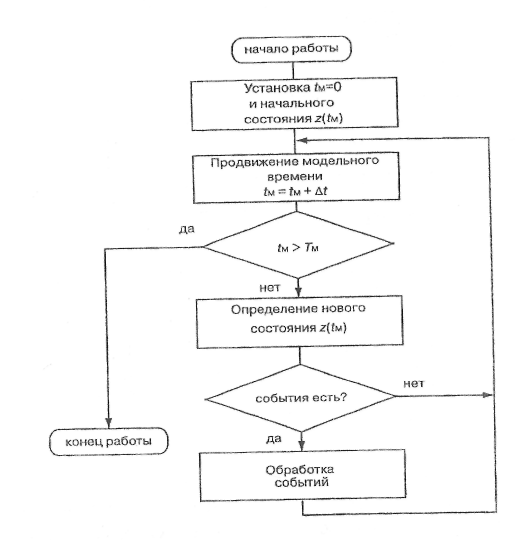
Рис. 3.2. Алгоритм моделирования с постоянным шагом

3.2.2. МЕТОД ОСОБЫХ СОСТОЯНИЙ

В модели, построенной по "принципу Sz" изменение времени наступа­ет в момент смены состояния системы, и последовательность моментов системного времени имеет вид: t1=tz1, t2=tz2, t3=tz3, t4=tz4= tz5, t5=tz6, т.е. моменты времени tn (δz) непосредственно связаны с моментами появления событий в системе Si.

При моделировании по особым состояниям системное время каждый раз изменяется на величину, строго соответствующую интервалу времени до момента наступления очередного события. В этом случае события обрабатываются в порядке их наступления, а одновременно наступившими считаются только те, которые являются одновременными в действительности.

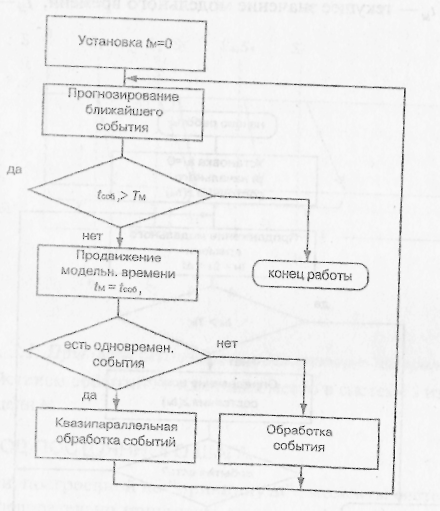
Рис, 3,3. Алгоритм моделирования по особым состояниям

Метод моделирования по особым состояниям сложнее в реализации, так как для него требуется разработка специальной процедуры планирования событий (так называемого календаря событий).

Моделирование по особым состояниям целесообразно использовать.

если:

•события распределяются во времени неравномерно или интервалы

между ними велики;

•предъявляются повышенные требования к точности определения взаимного положения событий во времени;

•необходимо реализовать квазипараллельную обработку одновременных событий. Дополнительное достоинство метода заключается в том, что он позволяет экономить машинное время, особенно при моделировании систем периодического действия, в которых события длительное время могут не наступать.

Обобщенная схема алгоритма моделирования по особым состояниям представлена на рис. 3.3 (t_сoбi - прогнозируемый момент наступления i-ro события).

Под "особыми состояниями", понимается всякие события, которые должны влиять на изменение модельного времени. На практике обычно вместо состояний рассматривают события, определяющие смену состояний моделируемого процесса. Например, для процесса ввода информации такой переход выполняется так:

событие - это ввод очередного символа; другими словами, ввод очередного символа "продвигает" модельное время на соответствующий интервал.

Если процесс подвержен влиянию случайных факторов, что на практике встречается очень часто, то они могут быть описаны с помощью случайных величин, распределенных по заданному закону. Для процесса ввода информации это может быть скорость ввода символов. В этом случае изменение модельного времени можно увязать с вводом очередного символа. Логика работы такой модели будет соответствовать рассмотренному алгоритму. Прогноз времени ввода очередного символа выполняется на основе функции распределения соответствующей случайной величины. Так, если скорость ввода символов подчиняется нормальному закону с параметрами т и d, то очередное i-e значение модельного времени tM_i,. определяется следующим образом:

(3.5)

В этом выражении слагаемое norm(m, d) означает обращение к генератору случайных чисел, распределенных по нормальному закону.

Таким образом, выбор механизма изменения модельного времени определяет и технологию реализации имитационной модели. Причем, на выбор метода моделирования влияет целый ряд факторов, однако определяющим является тип моделируемой системы: для дискретных систем, события в которых распределены во времени неравномерно, более удобным является изменение модельного времени по особым состояниям.

Если в модели должны быть представлены компоненты реальной системы, работа которых измеряется в разных единицах времени, то они должны быть предварительно приведены к единому масштабу.