3. Марковские модели. Процесс размножения и гибели как модель Марковского случайного процесса.

1.2.МАРКОВСКИЕ МОДЕЛИ

В теории СМО к наиболее изученным и исследованным относятся модели, у которых случайный процесс функционирования относится к классу марковских процессов, т.е. марковские модели.

Случайный процесс называется марковским, если вероятность любого состояния системы Е в будущем зависит только от состояния в настоящем и не зависит от того, когда и каким образом система пришла в это состояние. Описывающий поведение системы процесс z(t) называется цепью Маркова,

Описать процесс - значит определить вероятность того, что в момент времени t система находится в том или ином состоянии.

Для случайных процессов с дискретным временем изменения состояний происходят только в определенные моменты времени t₀,1₁...,t_k. Переходы описывают вероятностями переходов (Р_ij).

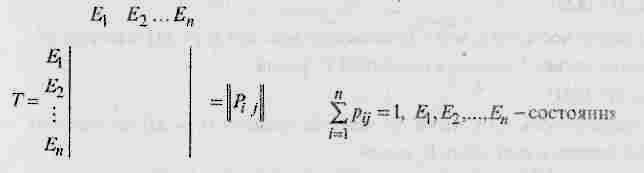
Для марковских процессов с непрерывным временем промежуток времени между переходами из одного состояния в другое случайно. Вероятность перехода из E_i → E_j не может быть задана. Вместо вероятностей вводится параметр, называемый интенсивностью перехода q_ij:

(предел отношения вероятности перехода из E_j Р_ij (∆t) за промежуток ∆t к длине ∆t (i≠j)).

Если Р_ij или q_ij постоянны и не зависят от момента времени t_k или ∆t (когда начинается), то марковский процесс называется однородным.

1.2.1. ЭЛЕМЕНТЫ ТЕОРИИ ПРОЦЕССОВ ГИБЕЛИ И РАЗМНОЖЕНИЯ

Среди классов марковских процессов с непрерывным временем интерес представляет частный класс процессов размножения и гибели, в которых состояние системы за любой бесконечно малый промежуток времени изменяется не больше, чем на единицу [2].

Обозначим через Е_к состояние системы, когда в ней содержится k заявок. И будем рассматривать переход системы лишь в соседние состояния Е_к , и Е_к+1. (рис.5). Обозначим через λ_к - интенсивность размножения, она характеризует среднюю скорость рождений (т.е. поступления новых заявок) в состоянии Е_к. Аналогично, через μ_к обозначим интенсивность гибели, задающую скорость, с которой происходит гибель (т.е. уход заявок из системы после обслуживания) в состоянии Е_к. Заметим, что интенсивности размножения и гибели не зависят от времени, а зависит только от состояния Е_к. Более точно, некоторый процесс представляет собой процесс размножения и гибели, если он является однородной цепью Маркова с множеством состояний {0,1,2, ..}, если рождение и гибель являются независимыми событиями и если выполняются следующие условия:

1) вероятность того, что в промежутке времени поступит только 1 заявка, в состоянии Е_к равна

2) вероятность того, что в промежутки временизакончит обслуживание только 1 заявка, в состоянии Е_к равна

3) вероятность того, что в промежутке времени не поступит ни одной заявки, в состоянии Е_к равна

4) вероятность того, что в промежутке временини одна заявка не закончит обслуживание в состоянии Е_к равна

Согласно этим условиям можно ввести предположение кратных событий: кратные рождения, кратные гибели и одновременные рождения и гибели в течении малого промежутка времени имеют вероятность бесконечно малую, порядка 0(∆t).

Определим вероятность того, что в некоторый момент времени t в системе находится k заявок и обозначим эту величину P_k(t).

Рассмотрим возможные изменения количества заявок в системе в промежутке времени (t,t + ∆t). В момент t + ∆t система будет находится в состоянии Е_к, если произошло одно из трех (взаимно исключающих и исчерпывающих все возможности) событий:

1. в момент времени t количество заявок было равно k и в течении времени (t,t+∆t) не произошло изменения состояния;

2. в момент времени t количество заявок было равно k-1 и в течении времени (t,t+∆t) поступила еще одна заявка (рождение);

3. в момент времени t количество заявок было равно k+1 и в течении времени (t,t+∆t) закончила обслуживание одна заявка (гибель).

Рис.1.5. Возможные переходы в состояние Е

На рис. 1.5. представлены эти три возможности. Вероятность первого события равна вероятности P_k(t) того, что в момент времени t процесс находится в состоянии Е_k , умноженной на вероятность P_k,k(∆t) перехода в течении времени ∆t; из состояния Е_к в состояние Е_к (т.е. на вероятность отсутствия на интервале ∆t рождения или гибели). Эта возможность описывается первым слагаемым в правой части написанного ниже равенства (14). Второе II третье слагаемые в правой части этого равенства соответствуют остальным двум указанным выше событиям. Переходы в состояние Е_к из состояний, не являющихся соседними не рассматриваются, т.к. предполагается, что вероятности таких событий в промежутке времени ∆t; имеют порядок 0(∆t). Таким образом можно записать

Эти три вероятности можно складывать, потому что соответствующие события, очевидно взаимно исключают друг друга. Ясно, что равенство (14) имеет смысл только при k≥1. Граничное равенство при k=0 имеет, в частности, следующий вид

(15)

Кроме того, в момент времени t все возможные состояния должны удовлетворять условию:

(16)

Теперь воспользуемся предположениями 1), 2), 3), 4) (стр.16) для вычисления коэффициентов, входящих в систему уравнений (14) - (15). Это приведет рассматриваемую систему к виду

В уравнении (18) использовано следующее предположение: если в системе нет ни одной заявки, то не может произойти гибели (т.е. μ₀=0), но может произойти рождениеРаскрывая скобки в правых частях (17) и (18) получаем:

Выделяя теперь Р_к (t) из обеих частей в обоих равенствах и деля на ∆t, приходим к уравнениям:

Переходя к пределу при ∆t→0, видим, что левые части в уравнениях (19) и (20) представляют собой производные от P_k(t) по t, а член стремится к нулю. Следовательно, окончательно уравнения записываются в виде:

(21)

Формулы для определения вероятностей состояний, полученные в результате решения уравнений Колмогорова (21) имеют вид:

Эти формулы часто используются при решении задач теории массового обслуживания.

Уравнения (21) являются искомой системой дифференциально-разностных уравнений, описывающих динамику рассматриваемого вероятностного процесса. Решение этой системы представляет собой характеристику Р_к (t). На рис. 1.6. показан граф состояний модели размножения и гибели.

Puc. 1.6. Граф состояний модели размножения и гибели

Граф позволяет наглядно описать процесс перехода системы из одного состояния в другое. Ребра указывают возможные переходы, а приписанные им числа соответствуют интенсивностям размножения и гибели.

12.2. ПУАССОНОВСКИЙ ПРОЦЕСС КАК ПРОЦЕСС ЧИСТОГО РАЗМНОЖЕНИЯ

Рассмотрим простейший процесс чистого размножения, который определяется как процесс, для которого μ_к=0 при всех k. Для упрощения предположим, что λ_к = λ для всех k-0,1,2,... . Подставляем эти значения в уравнения (21) получаем

(22)

Предположим также, что процесс начинается в нулевой момент времени при нуле членов, т.е.

(23)

Отсюда для P₀(t) получаем решение

(24)

Подставляя это решение в уравнение

(22)

при к=1 приходим к уравнению Решение этого дифференциального уравнения, 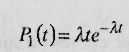очевидно имеет вид

Далее по индукции в качестве решения уравнения (22) находим

(25)

Распределение вероятностей, задаваемое формулой (25) носит название закона распределения Пуассона, а случайный процесс, управляемый этим распределением - процессом Пуассона.

Таким образом процесс чистого размножения с постоянной интенсивностью λ приводит к последовательности рождений, образующих Пуассоновский процесс.

Условимся рассматривать процесс Пуассона как модель нестационарного потока заявок, поступающих в СМО. Тогда в уравнении (25) λ означает интенсивность потока заявок, а величина Р_к (t) при начальных условиях (23) означает вероятность появления k заявок в промежутке времени (0, t).

На рис. 1.7. показана форма распределения Пуассона для некоторых частных значений λ_t

Рис. 1.7. Распределение Пуассона

Математическое ожидание М и дисперсия D распределения Пуассона

(26)

Среднее значение и дисперсия числа поступающих заявок для распределения Пуассона одинаковы.

Формула (24) означает, что в течение промежутка времени длительностью t не появится ни одна заявка. Обозначим через ε длину промежутка времени, в течение которого не появится ни одной заявки. Тогда вероятность того, что эта длина окажется больше, чем t, равна P₀(t) и тем самым p(ε≥)=P₀(t)=e^-λt. Обозначим A(t) - функцию распределения вероятностей. Т.к. A(t) является вероятностью того, что время между соседними заявками не превышает t, то

(27)

Дифференцируя это равенство, находим плотность распределения

(28)

Приведенные равенства (27) и (28) описывают экспоненциальное или показательное распределение. Графики распределения вероятностей соответствующие различным значениям λ приведены на рис1.8.

Рис. 1.8. Плотность распределения интервалов времени между заявками

Равенства (27) и (28) показывают, что для Пуассоновского потока интервалы времени между соседними заявками распределены по экспоненциальному закону; обычно говорят, что пуассоновский поток заявок характеризуется экспоненциальным распределением интервалов времени между заявками.