4.Построение эпюр Qy и Mx для всей балки.

Откладываем перпендикулярно от оси абсцисс в удобном для пользования масштабе значения Q_y и M_x , возникающие в харак­терных и промежуточных сечениях каждого участка. Соединяем концы полученных ординат линиями, соответствующими законам изменения Q_y и M_x на этих участках; строим эпюры Q_y и M_x для всей балки (рис. 13, в,г).

5. Подбор поперечных сечений балок.

5.1. Подбор двутавра

Опасным явля­ется сечение «B», где возникает наибольший по абсолютной величи­не |M_max |= 41,6 кНм. Двутавровое сечение балки подбираем из ус­ловия прочности при изгибе при расчетном сопротивлении мате­риала R = 20010³ кН/м² (сталь):

σ_max 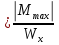≤ R .

Откуда требуемый момент сопротивления W_x равен:

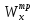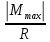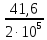= == 20,8∙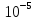м³ = 208 см³.

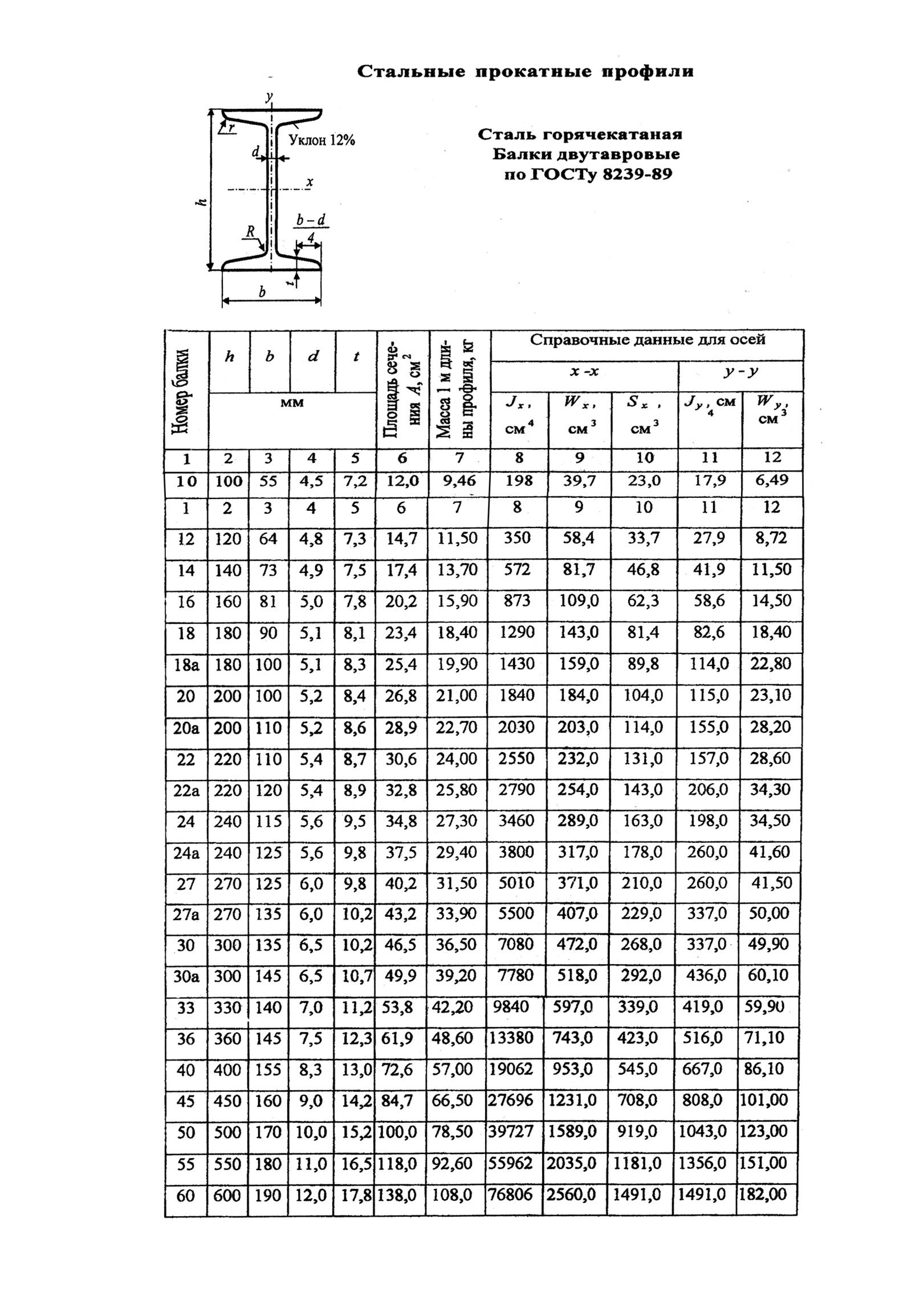
В сортаменте (ГОСТ 823989), (см. Приложение), наш требуемый момент сопротивления 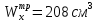находится между значениямиW_x=203 см³ (двутавр №20а) и W_x=232 см³ (двутавр №22).

Возьмём двутавр №20а и определим для него максимальное напряжение:

σ_max 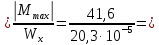204,9 ∙ 10³ кН/м².

Перенапряжение составляет:

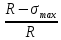∆= ∙100% = 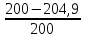∙100% = 2,5%.

Возьмём двутавр №22 и определим для него максимальное напряжение:

σ_max 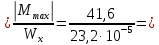179,3 ∙ 10³ кН/м².

Недогрузка составляет:

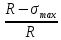∆= ∙100% = 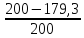∙100% = 10,3%.

По СНиП в практических расчетах допускается разница ∆= ±5%. Окончательно принимаем двутавр №20а площадью A=28,9 см².

5.2. Подбор прямоугольного, квадратного, круглого и кольцевого сечений.

В нашем примере опасным является сечение «B», где возникает наибольший по абсолютной величи­не |M_max |= 41,6 кНм.

Прямоугольное сечение балки подбираем из условия прочности при рас­четном сопротивлении R = 20010³ кН/м². При s=15 соотношение h/b = 2,5. В пункте 5.1 из условия прочности для опасного сечения получено значение момента сопротивления 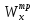=208 см³.

Момент сопротивления прямоугольного сечения равен:

= =

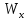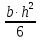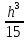
Приравняв его к 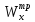, получим:

h =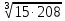=14,61 см.

   

   b = h/2,5 = 14,61/2,5 = 5,8 см.

Округляя, принимаем брус поперечным сечением hb = 0,150,06 (м).

Площадь прямоугольного сечения будет равна: 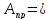b∙h =0,15 ∙ 0,06 = 0,009 .

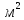Квадратное сечение при R = 20010³ кН/м² и b=h:

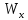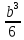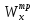= ==208 см³.

Отсюда: b =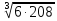=10,77 см. Округлим до 11 см., т.е.b=h=0,11м.

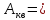
Площадь квадратного сечения будет равна: 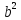= = 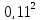0,0121 .

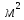Круглое сплошное сечение при R = 20010³ кН/м² имеем:

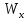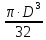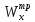= ==208 см³.

Отсюда: D =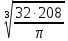=12,845 см. Округлим до 13 см., т.е.D=0,13м.

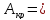
Площадь круглого сплошного сечения будет равна: 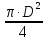= = 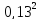0,0169 .

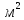Кольцевое сечение при R = 20010³ кН/м² и t= 4 имеем:

W_x=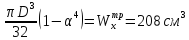 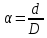= 1– 0,1∙ t = 0,6

D =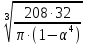== 13,45см.

d = α∙D = 0,6∙13,45 = 8,07 см.

Округляем оба диаметра до значений: d = 0,08 м; D = 0,14 м.

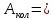
Площадь кольцевого сечения будет равна: 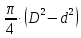= 0,0104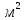

Так как вес балки прямо пропорционален её площади, то сравним площади балок разных поперечных сечений с площадью двутавра (Табл.9).

Таблица 9.

Форма сечения	Двутавр	Прямоугольник	Квадрат	Круг	Кольцо
Площадь сечения A, м2	0,00289	0,009	0,0121	0,0169	0,0104
Отношение площадей A/	1	3,1	4,2	5,8	3,6

По данным Табл.9 можно сделать вывод, что самым рациональным сечением ( при условии равнопрочности) является двутавр. Самое невыгодное – круглое сечение, так как используется большее количество материала.

.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов /

Учеб. для вузов. –М.: Высш. шк., 2005.-560 с.

2. Миролюбов И.Н. Пособие к решению задач по сопротивлению материалов /

И.Н. Миролюбов [ и др.]. – СПб.: Лань, 2009. – 512 с.

3. Справочник по сопротивлению материалов / Писаренко Г.С., Яковлев А.П., Матвееев В.В. – Киев: Наук. думка, 1988. – 736 с.

4. Филатов А.П., Вершинин П.В. Сопротивление материалов: Конспект лекций (часть 1) – Самара: СамГУПС, 2012. - 67с.

Приложение.