
- •Самарский государственный университет путей сообщения
- •Сопротивление материалов расчет статически определимых балок на прочность при изгибе
- •1. Основные понятия
- •Условие прочности при изгибе
- •2. Задание к расчетно-графической работе
- •3. Пример выполнения расчетно-графической работы Задача 1.
- •Задача 2.
- •Определение опорных реакций.
- •2. Определение количества участков балки.
- •3. Составление аналитических выражений внутренних усилий Qy и Mx.
- •4.Построение эпюр Qy и Mx для всей балки.
- •5. Подбор поперечных сечений балок.
- •5.1. Подбор двутавра
- •5.2. Подбор прямоугольного, квадратного, круглого и кольцевого сечений.
МИНИСТЕРСТВО ТРАНСПОРТА РФ
федеральное агентство железнодорожного транспорта
Самарский государственный университет путей сообщения
Кафедра "Строительные конструкции и материалы"
Сопротивление материалов расчет статически определимых балок на прочность при изгибе
Варианты заданий и методические указания по выполнению
расчетно-графической работы для студентов специальностей:
271501.65 – Строительство железных дорог, мостов и
транспортных тоннелей.
190109.65 – Наземные транспортно-технологические
средства.
190300.65 – Подвижной состав железных дорог
Составители: В.А.Довгий
А.П.Филатов
Самара 2012
УДК 620.10
Сопротивление материалов. Расчёт статически определимых балок на прочность при изгибе. Варианты заданий и методические указания по выполнению расчетно-графической работы / Составители: В.А.Довгий, А.П.Филатов. – Самара: СамГУПС, 2012. - 19с.
Утверждено на заседании кафедры 24 апреля 2012 г., протокол № 8.
Печатаются по решению редакционно-издательского совета университета.
Методические указания составленыв соответствии с программой курса "Сопротивление материалов" для студентов специальностей: 271501.65 – Строительство железных дорог, мостов и транспортных тоннелей, 190109.65 – Наземные транспортно-технологические средства, 190300.65 – Подвижной состав железных дорог.
.
Составители: Владимир Анатольевич Довгий, ст. преподаватель,
Анатолий Петрович Филатов, к. т. н., доцент.
Рецензенты: к.т.н., профессор СамГУПС И.Е. Сеськин
д. т. н., профессор кафедры "Высшая математика"
СГАУ В.В. Любимов
Редактор: И.М. Егорова
Компьютерная вёрстка: Е.А. Самсонова
Подписано в печать 12.10.2012. Формат 60х90 1/16
Бумага писчая. Печать оперативная. Усл. п. л. 1,2.
Тираж 250 экз. Заказ №………
© Самарский государственный университет путей сообщения, 2012
1. Основные понятия
Прямой брус испытывает деформацию изгиба, если он нагружен силами или парами сил в плоскости, проходящей через ось бруса, а сами силы или пары сил действуют перпендикулярно этой оси (рис. 1). Брус под действием этих сил изогнётся, его ось искривится, а в поперечных сечениях появятся изгибающий момент М и поперечная сила Q. Прямолинейный брус, работающий на изгиб, называется балкой.
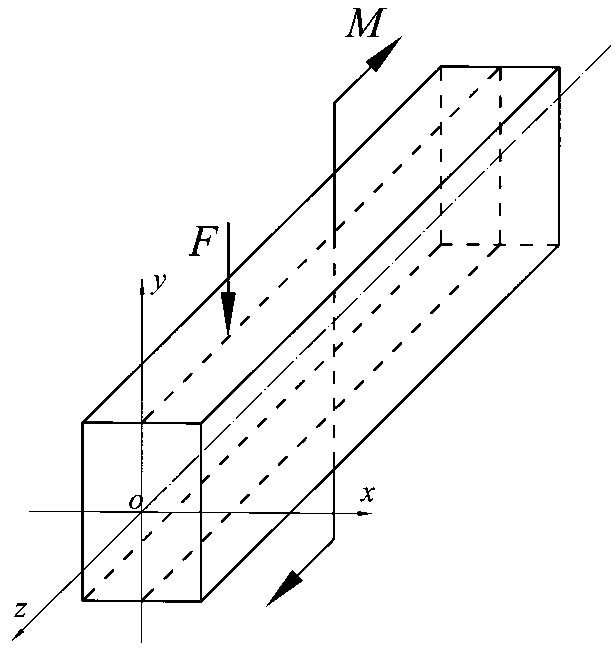
Рассмотрим в условиях статического равновесия балку, нагруженную сосредоточенной силой F, распределеннойнагрузкой с интенсивностью q=q(z) и парой сил M (рис.2 а). Применяя метод сечений, разделим брус мысленно на две части (рис. 2 б).
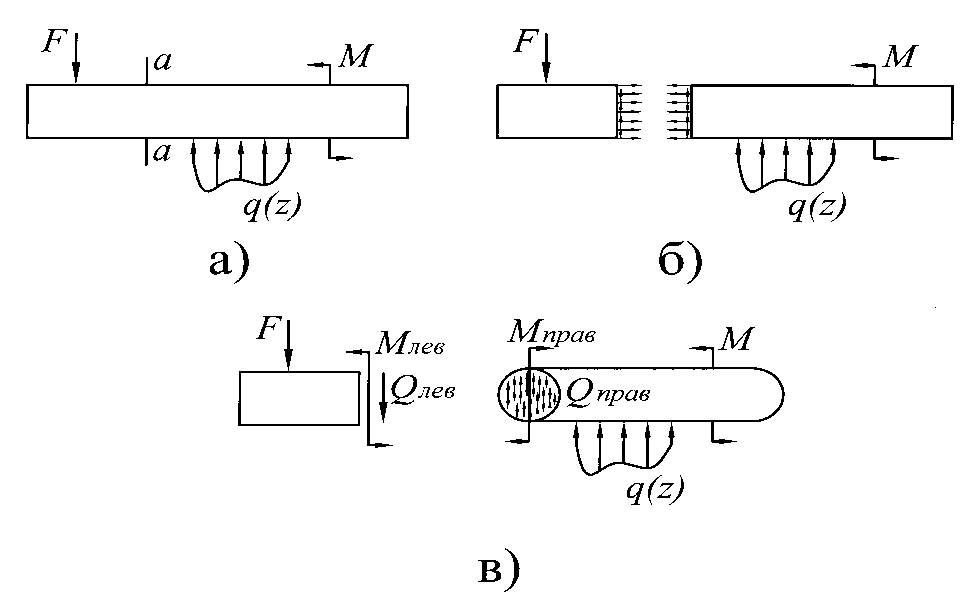
Рис.1
Рис.2
Для того чтобы каждая из частей находилась в равновесии, в сечении необходимо приложить поперечную силу Q и изгибающий момент М (рис.2 в). Эти силовые факторы определяются из уравнений равновесия одной из частей бруса по следующим правилам:
поперечная сила Q в каком либо сечении балки равна сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на направление перпендикулярное оси балки;
изгибающий момент М в каком либо сечении балки равен сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно центра тяжести этого сечения.
Правила знаков при определении поперечной силы и изгибающего момента.
Поперечная сила Q считается положительной, если внешняя сила стремится повернуть рассматриваемую часть балки относительно сечения по часовой стрелке, если внешняя сила стремится повернуть рассматриваемую часть балки против часовой стрелки, то Q принимается отрицательной. Эти правила знаков можно представить схемой (рис. 3)
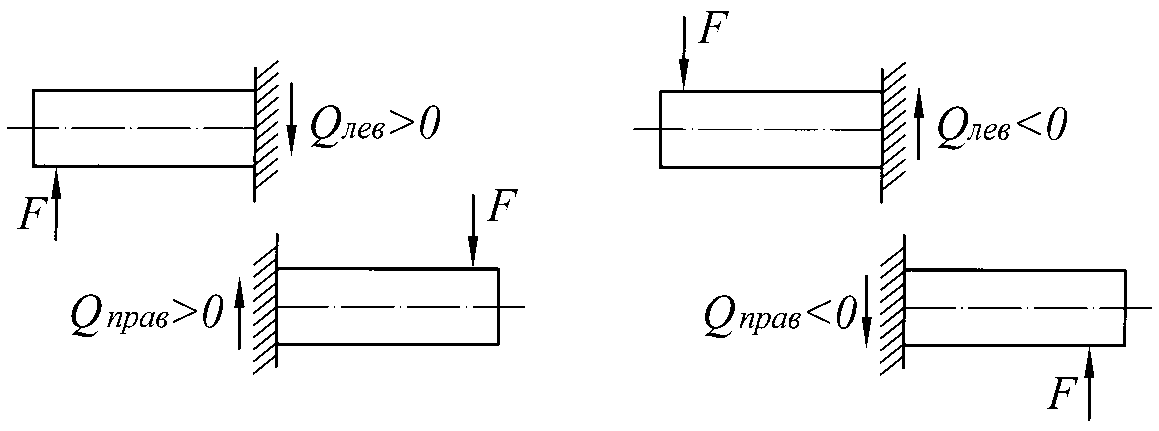
Рис.3
Изгибающий момент считается положительным, если внешние силы изгибают балку выпуклостью вниз, если выпуклость балки будет вверх, то момент будет отрицательным (рис. 4).
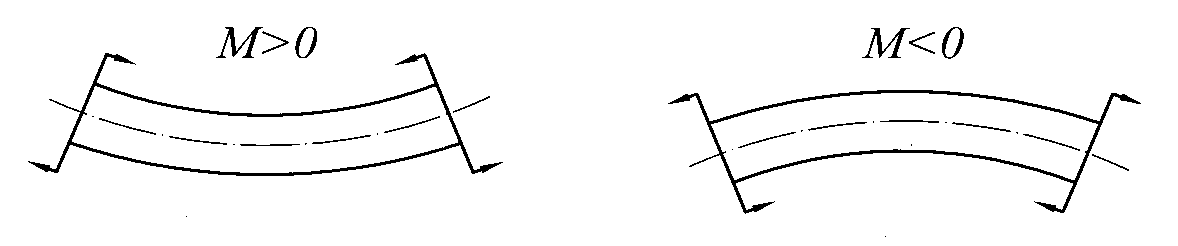
Рис.4
Графики зависимостей Q=Q(z) и M=M(z), называются эпюрами поперечных сил и изгибающих моментов. Положительные значения поперечных сил откладываются
вверх от продольной оси балки. Положительные значения изгибающих моментов инженеры-машиностроители откладывают вверх от оси балки, а инженеры-строители вниз от оси балки, т.е. ординаты эпюры моментов во втором случае располагаются со стороны растянутого волокна балки.
При изгибе между интенсивностью распределённой нагрузки q, поперечной силой Q и изгибающим моментом M существуют дифференциальные зависимости, с помощью которых можно проверить правильность построения эпюр внутренних усилий:
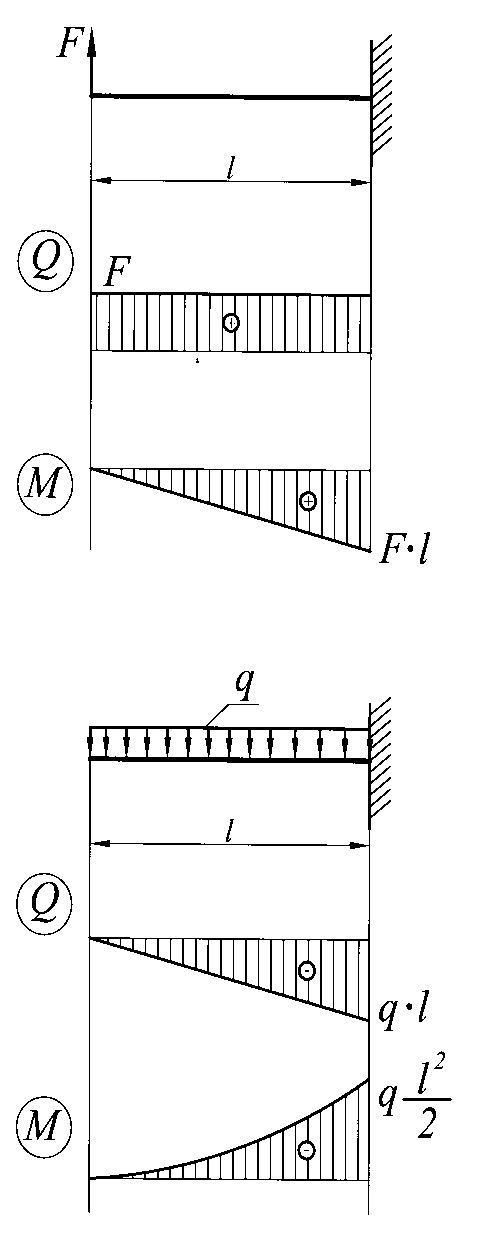
1. На участке, где нет распределённой нагрузки (q=0) поперечная сила постоянна, изгибающий момент изменяется по линейной зависимости (рис.5). В частном случае может быть одновременно q=0 и Q=0, тогда изгибающий момент постоянен.
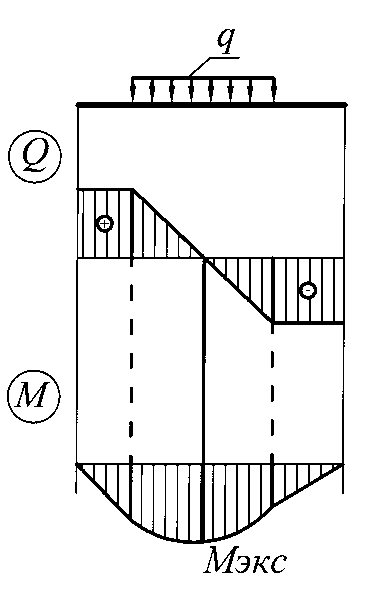
2. На участке, где имеется равномерно распределённая нагрузка, поперечная сила Q изменяется по линейной зависимости, изгибающий момент – по квадратичной зависимости, выпуклость которой обращена в сторону действия распределенной нагрузки q (рис.5 б, в).
Если на этом участке поперечная сила в некотором сечении равна нулю, то изгибающий момент в этом сечении достигает экстремального значения – максимума или минимума.
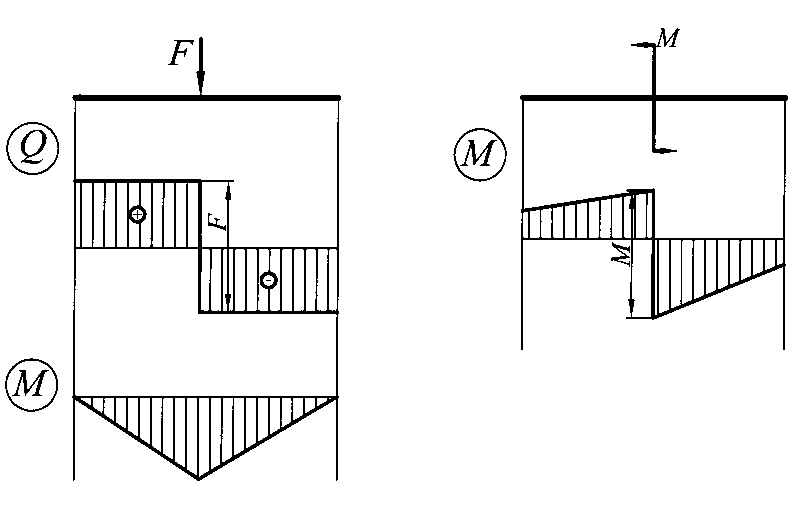
3. В сечении, где приложена сосредоточенная сила F, на эпюре Q будет скачок, равный величине этой силы и направленной в ту же сторону, а эпюра моментов будет иметь излом, направленный в сторону действия силы F (рис.5 а, г).
4. В сечении, где приложен сосредоточенный изгибающий момент, на эпюре М будет скачок, равный величине этого момента. Направление скачка будет вверх, если сосредоточенный момент направлен по ходу часовой стрелки, и вниз, если против хода часовой стрелки (рис.5 д).
5. Если на участке балки Q>0, то момент на этом участке возрастает, если Q<0, то момент убывает, если Q=0, М= const.
а) б)
в) г) д)
Рис.5
