3.5. Деформации участков стержня и перемещения сечений. Условия жесткости

При осевом растяжении или сжатии до предела пропорциональности σ_pr справедлив закон Гука, т.е. закон о прямо пропорциональной зависимости между нормальными напряжениями  и продольными относительными деформациями :

(3.10)

или (3.11)

Здесь Е – коэффициент пропорциональности в законе Гука имеет размерность напряжения и называется модулем упругости первого рода, характеризующим упругие свойства материала, илимодулем Юнга.

Относительной продольной деформациейназывается отношение абсолютной продольной деформации участкастержня к длине этого участка до деформации:

(3.12)

Относительная поперечная деформация будет равна: ' = = b/b, гдеb=b₁–b.

Отношение относительной поперечной деформации ' к относительной продольной деформации, взятое по модулю, есть для каждого материала величина постоянная и называется коэффициентом Пуассона:

Определение абсолютной деформации участка бруса

В формулу (3.11) вместо иподставим выражения (3.1) и (3.12):

Отсюда получим формулу для определения абсолютного удлинения (или укорочения) участка стержня длиной :

(3.13)

В формуле (3.13) произведение ЕА называетсяжесткостью бруса при растяжении или сжатии,которая измеряется в кН, или в МН.

По этой формуле определяется абсолютная деформация , если на участке продольная сила постоянна. В случае, когда на участке продольная сила переменна, она определяется по формуле:

(3.14)

где N(х) – функция продольной силы по длине участка.

В частности, по этой же формуле вычисляется абсолютная деформация при учете собственного веса для вертикального бруса, когда вес одного погонного метра бруса входит в выражение для N(х) как интенсивность распределенной нагрузки, направленной вниз, параллельно оси бруса:

,

где – плотность материала бруса, кН/м³, Н/м³; А – площадь поперечного сечения бруса, м².

Определение перемещений сечений бруса

Определим горизонтальное перемещение точки аоси бруса (рис. 3.5) –u_a: оно равно абсолютной деформации части брусааd, заключенной между заделкой и сечением, проведенным через точку, т.е.

В свою очередь удлинение участка аdсостоит из удлинений отдельных грузовых участков 1, 2 и 3:

(3.15)

Продольные силы на рассматриваемых участках:

Следовательно,

Тогда

Аналогично можно определить перемещение любого сечения бруса и сформулировать следующее правило:

перемещение любого сечения j стержня при растяжении–сжатии определяется как сумма абсолютных деформаций n грузовых участков, заключенных между рассматриваемым и неподвижным (закрепленным) сечениями, т.е.

(3.16)

Условие жесткости бруса запишется в следующем виде:

, (3.17)

где – наибольшее значение перемещения сечения, взятое по модулю из эпюры перемещений;u– допускаемое значение перемещения сечения для данной конструкции или ее элемента, устанавливаемое в нормах.

ПРИМЕР 3.2

Требуется построить эпюру N для бруса, изображенного на рис. 3.6а и подобрать площадь сечения А и размер сторон квадратного сечения из условия жесткости при

Е = 0,2710⁵ МПа,u= 2 мм = 210^–3 м.

РЕШЕНИЕ

1. В данной задаче, как и в предыдущей, нет необходимости определять реакцию заделки, так как один конец бруса свободный.

2. Разбиваем брус на грузовые участки 1, 2, 3.

3. В пределах каждого грузового участка проводим сечения на расстоянии x_iот начала участка, т.е. используем местную систему координат.

4. Используя рабочее правило и принятое правило знаков, в каждом сечении записываем функцию продольной силы N_i(х_i) (в таком случае рекомендуется рукой или бумагой закрывать отбрасываемую часть бруса, чтобы не делать дополнительных рисунков). При этом рассматриваем свободную часть бруса.

При

При

При

При

5. По вычисленным результатам строим эпюру N (рис. 3.3б).

Анализ построенной эпюры N позволяет выделить следующие особенности:

– в сечении, где приложена сосредоточенная сила F, параллельная оси бруса, имеется скачок, равный этой силе;

– на грузовых участках, где действуют равномерно распределенные нагрузки интенсивностью q, на эпюре N имеются наклонные прямые, тангенсы углов между этими прямыми и осью бруса равны интенсивности распределенной по длине нагрузки q;

– на тех грузовых участках, где отсутствует распределенная нагрузка, эпюра N постоянна.

6. Определим перемещения характерных сечений и построим эпюру перемещений при А = const:

u_A= 0 (так как здесь защемление, препятствующее вертикальным перемещениям).

Используя полученные результаты, строим эпюру перемещений сечений (см. рис. 3.3в), из которой видим, что Используя равенствополучаем

Отсюда А = 

При А = сторона квадратного поперечного сечения будет равна а =

ПРИМЕР 3.3

Для бруса, изображенного на рис. 3.7а требуется:

– построить эпюру Nбез учета собственного веса;

– подобрать площади поперечных сечений из условий прочности;

– построить эпюры продольных сил N, нормальных напряжений  и перемещений сечений u с учетом собственного веса бруса и проверить прочность и жесткость при следующих данных:

R_t= 0,9 МПа = 0,910³кПа.

;= 25 кН/м³;u= 0,510^–3м.

РЕШЕНИЕ

1. Как и в предыдущем примере, опорную реакцию не определяем, так как один конец бруса свободен.

2. Выделяем грузовые участки стержня 1, 2, 3.

3. В этом примере эпюру N будем строить, записывая их функции на каждом грузовом участке, используя рабочее правило, приведенное в конце примера 3.1 (с. 17).

Расчет без учета собственного веса бруса

x₂ = 0, N₂(0) = 40 кН;

х₂ = 1,2 м, N₂(1,2) = 16 кН;

N₃(x₃) = – F₃ + F₂–F₁ – q_n )1,2 + x₃) = 

 = –100 +140 – 120 – 20(1,2 +x₃) = –104 – 20x₃.

x₃ = 0,N₃(0) = –104 кН;

х₃= 1,2 м, N₃(1,2) = –144 кН.

По вычисленным значениям строим эпюру продольных сил N (рис. 3.7б).

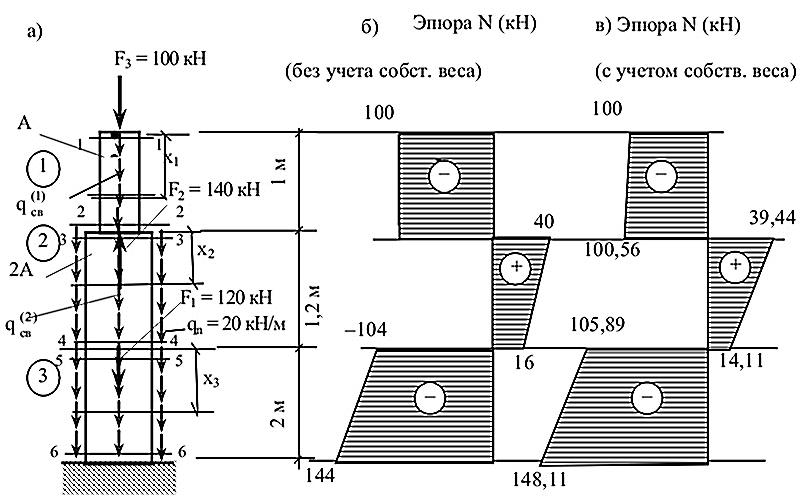
Рис. 3.7

4. Из условий прочности (3.3), используя эпюру N, построенную без учета собственного веса, определяем требуемую площадь поперечного сечения бруса, соблюдая заданное соотношение площадей на отдельных участках (рис. 3.7а). По условию задачи на участках 2 и 3 (нижняя ступень) площади сечения одинаковы и равны 2А. Для этих участков из эпюры N имеем:

В условиях прочности (3.3) приравняем и получаем:

На участке 1 (верхняя ступень) площадь сечения по условию задачи должна быть равна А. Из эпюры N для этого участка имеем:

.

Площадь поперечного сечения будет равна:

Из трех найденных значений А выбираем большую:

, 2А = 44,4410^–3м².