3.7. Контрольные вопросы по теме

1. В чем заключается суть метода сечений при определении внутренних усилий, в частности, при определении продольных сил?

2. Приведите рабочее правило для определения продольных сил в поперечных сечениях стержней и правило знаков для них.

3. Как определяется нормальное напряжение в поперечном сечении бруса при растяжении–сжатии?

4. Что такое расчетное сопротивление материала?

5. Как записываются условия прочности при растяжении-сжатии для пластичных и хрупких материалов?

6. Как производится подбор требуемой площади поперечного сечения бруса из условия прочности?

7. Как формулируется закон Гука? Как он записывается для случая растяжения–сжатия?

8. Как определяется абсолютная деформация бруса при осевом растяжении–сжатии при наличии распределенной нагрузки на грузовом участке и при ее отсутствии?

9. Какие системы называются статически неопределимыми? Каков порядок их решения?

10. Назовите характеристики прочности материала. Как они определяются с помощью диаграммы растяжения для низкоуглеродистой стали?

11. Назовите характеристики пластичности материала. Как они определяются?

4. Основы теории напряженно-деформированного состояния в точке. Теории прочности

4.1. Главные площадки и главные напряжения. Классификация напряженных состояний

Значения нормальных и касательных напряжений на произвольных площадках, проходящих через какую-либо точку тела, зависят от положения этих площадок.

Совокупность нормальных и касательных напряжений, действующих на различных площадках, проходящих через заданную точку, называется напряженным состоянием в этой точке.

В курсе теории упругости доказано, что в окрестности любой точки можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения будут отсутствовать. Такие площадки называются главными. Нормальные напряжения на главных площадках принимают экстремальные значения, называются главными напряжениямии обозначаются: σ₁, σ₂, σ₃. Здесь σ₁– наибольшее (в алгебраическом смысле) главное напряжение, σ₃– наименьшее, а σ₂– промежуточное, т.е. σ₁≥ σ₂≥ σ₃.

На рис. 4.1а показаны три взаимно перпендикулярные произвольные площадки, на гранях которых действуют нормальные и касательные напряжения. Нормальные напряжения показаны растягивающими, т.е. положительными. Касательные напряжения (на каждой грани по два) показаны с двумя индексами: первый индекс указывает параллельно какой оси координат действует, а второй – на грани с какой нормалью. В общем случае напряженное состояние в точке описывается тензором напряжений

.

На рис. 4.1б показан параллелепипед с бесконечно малыми размерами сторон, грани которого являются главными площадками, так как на них отсутствуют касательные напряжения. В зависимости от наличия отличных от нуля главных напряжений на главных площадках различают три вида напряженных состояний:

1. Если все три главных напряжения отличны от нуля, то имеет место в данной точкеобъемноеилипространственное напряженное состояние(ОНС) (рис. 4.1б).

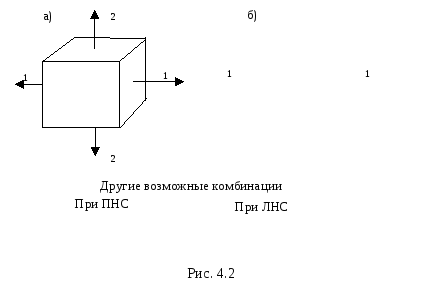
2. В том случае, когда два главных напряжения отличны от нуля, а одно равно нулю – имеет место плоское напряженное состояние(ПНС) (рис. 4.2а).

3. Если только одно главное напряжение отлично от нуля, а два других равны нулю, имеет местоодноосное(линейное) напряженное состояние(ЛНС) (рис. 4.2б).

Наиболее простым и наглядным случаем одноосного (линейного) напряженного состояния является центральное растяжение–сжатие стержней. Определение напряжений на наклонных площадках при ЛНС было исследовано в п. 3.3 предыдущей главы.