
- •Санкт-Петербургский государственный горный институт
- •Раздел 3.2 .Модель идеального вытеснения. 40
- •Раздел 3.4. Диффузионная модель 47
- •Раздел 5. Синтез моделей технологических объектов на базе их гидродинамических моделей и уравнений химической кинетики. 125
- •1. Введение. Основные понятия систем
- •1.1.Очень большая система
- •1.2.Общая структура сложных объектов систем и основные этапы моделирования.
- •1.2.1.Формализованное описание.
- •1.2.2.Математическое описание.
- •1.2.3.Моделирующий алгоритм.
- •2. Общие принципы и этапы построения математических моделей систем.
- •2.1. Структурный анализ и структурный синтез сложных технологических систем
- •2.2. Обобщенная структурная модель металлургического процесса.
- •3. Модели структуры потоков для технологических объектов.
- •3.1 Модель идеального перемешивания.
- •Применение преобразования Лапласа для анализа математических моделей.
- •Раздел 3.2 .Модель идеального вытеснения.
- •3.3. Ячеечная модель аппарата
- •Раздел 3.4. Диффузионная модель
- •Стационарный метод определения критерия Пекле.
- •3.5.Комбинированные модели
- •3.5.1.Модель с застойной зоной
- •3.5.2.Модель с байпасным потоком.
- •3.5.3.Последовательное соединение ячеек идеального вытеснения и идеального смешения.
- •3.5.4.Гидродинамические модели многофазных потоков.
- •3.6.Методы определения параметров моделей структуры потоков.
- •3.6.1. Характеристики кривых отклика аппаратов на возмущения с помощью моментов.
- •3.6.2. Связь передаточных функций с моментами кривых
- •3.6.3.Ячеечная модель
- •3.6.4.Диффузионная однопараметрическая модель
- •3.6.5.Вычисление моментов по экспериментальным данным.
- •3.6.6.Определение параметров гидродинамических моделей по экспериментальным данным путем решения обратной задачи методами нелинейного программирования.
- •4. Кинетические модели для описания химических превращений.
- •4.1.Основные закономерности химической кинетики
- •4.2. Методы определения параметров кинетических моделей.
- •4.2.1.Определение констант скорости параллельных реакций:
- •4.3.Определение кинетических констант сложных реакций методами нелинейного программирования.
- •4.4. Кинетика гетерогенных процессов.
- •4.4.1 Типы гетерогенных процессов
- •4.4.2.Основные стадии гетерогенных процессов.
- •4.4.3.Определение области протекания гетерогенного процесса.
- •Влияние формы межфазной поверхности раздела фаз на скорость гетерогенных процессов.
- •Раздел 5. Синтез моделей технологических объектов на базе их гидродинамических моделей и уравнений химической кинетики.
- •5.1. Модель идеального смешения
- •5.2.Модель идеального вытеснения:
- •5.3. Диффузионная модель
- •Литература
1.2.3.Моделирующий алгоритм.
Математическое описание служит исходным материалом для создания алгоритма, моделирующего исследуемый объект. Задачей моделирующего алгоритма является решение системы уравнений математического описания, что позволяет находить внутренние параметры математической модели при заданной совокупности внешних параметров. В процессе математического моделирования иногда встречаются задачи, в которых фиксируют определенные значения ряда внутренних параметров и требуется определить набор внешних параметров, обеспечивающих получение фиксированных внутренних параметров. Такие задачи возникают, например, при решении задач управления, когда для заданного режима работы объекта необходимо найти значения управляющих воздействий, обеспечивающих заданный режим функционирования объекта. Эта проблема не так проста, как кажется на первый взгляд. По существу это обратная задача, так как нужно искать набор управляющих воздействий, соответствующих заданному режиму.
Для решения систем уравнений математической модели в настоящее время имеются пакеты программ для решения дифференциальных уравнений как обыкновенных, так и в частных производных. В частности, такие возможности предоставляют известные системы Mathlab и Mathcad. Созданы также специализированные программные комплексы Aspen, HYSYS и ReactOp для решения математических моделей технологических объектов. Так что выбор моделирующего алгоритма в настоящее время сводится к четкой формулировке задачи, выбору внутренних и внешних переменных и соответствующего программного пакета.
2. Общие принципы и этапы построения математических моделей систем.
2.1. Структурный анализ и структурный синтез сложных технологических систем
Сложные системы характеризуются функцией, целью и структурой. Для выполнения цели функционирования система должна иметь необходимый набор элементов, объединенных внутренними связями и образующими структуру, необходимую для функционирования в направлении достижения поставленной цели. При этом каждый элемент рассматриваемой системы, может иметь в свою очередь сложный состав и характеризоваться своей собственной структурой, элементным составом и целью, которая не противоречит общей цели функционирования системы более высокого уровня. Для создания математических моделей, используемых для исследования поведения и свойств систем, используют обычно системный подход, состоящий из системного анализа и системного синтеза. В соответствии с этим подходом сложная система анализируется и расчленяется на боле простые системы, вплоть до элементарных процессов. Эта процедура называется системным анализом.
В процессе системного анализа реальная система и ее элементы упрощаются, схематизируются, и полученная схема описывается в зависимости от сложности явления с помощью основных физико-химических закономерностей и подходящего математического аппарата. В полученной таким образом модели должны быть учтены все основные черты рассматриваемого объекта, и вместе с тем, она не должна содержать мелких, второстепенных деталей, усложняющих ее и делающих затруднительным анализ.
На основании системного подхода выполняется анализ всех элементов системы, выясняется, какие элементарные процессы протекают при функционировании системы и ее элементов, составляется математическое описание отдельных элементарных процессов, а затем составляется общее математическое описание функционирования технологического объекта. Составление общего математического описания объекта производится на основании структуры объекта, с учетом характера связей между элементарными процессами, протекающими в объекте. Расчленение сложного процесса в объекте на элементарные стадии называется системным анализом процесса. Объединение математических описаний отдельных элементарных процессов в единое математическое описание объекта называется системным синтезом.
После построения модели необходимо проверить насколько верно описывает модель качественные и количественные характеристики объекта моделирования. Для этого проверяют адекватность модели. Адекватность модели проверяется путем сопоставления результатов моделирования с результатами наблюдения за характеристиками системы в процессе ее функционирования. Адекватность модели зависит от того, насколько справедливы упрощения, сделанные при формулировке модели. Если модель адекватна, ее можно использовать для дальнейшего анализа поведения моделируемого объекта и системы в целом. Если модель не адекватна, необходимо либо пересмотреть значения параметров модели. Это так называемая параметрическая идентификация. Либо пересмотреть структуру модели. Эта процедура называется структурной идентификацией модели. При построении модели используется блочная структура модели. В соответствии с этой структурой модель представляется в виде совокупности отдельных блоков, описывающих элементарные процессы в объекте. Блоки объединяются в модель в соответствии со структурой объекта.
Процессы в технологических объектах происходят, как правило, в движущихся многофазных потоках, они сопровождаются переносом тепла и массы движущимися потоками и сопровождаются химическими превращениями исходных исходного сырья в продукты переработки. Эти процессы обычно сопровождаются выделением или поглощением тепла. Для поддержания необходимого температурного режима к технологическому объекту подводится (или отводится) тепло из окружающей среды.
В соответствии с этим, структура технологического объекта как системы может быть представлена в следующем виде:
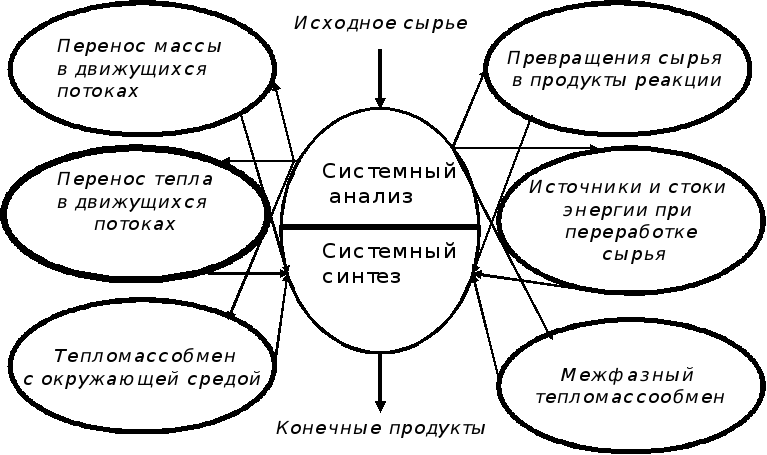
Рис.2.1. Структурная схема технологического объекта
