4.2. Методы определения параметров кинетических моделей.

Параметрами кинетических моделей являются предэкспоненциальные множители, энергии активации и порядки реакции по отдельным компонентам.

Порядки реакции по отдельным компонентам могут быть определены через стехиометрические коэффициенты отдельных стадий только в тех случаях, когда записанная последовательность стадий соответствует действительному механизму взаимодействия реагентов. В тех случаях, когда механизм неизвестен и не может быть записан в виде последовательности элементарных стадий, мы имеем дело с суммарным кинетическим уравнением, называемым уравнением формальной кинетики. В этом случае порядки реакции по компонентам могут быть дробными, что является следствием не учета отдельных быстро протекающих промежуточных стадий.

Кинетические параметры определяются, как правило, по экспериментальным данным, полученным в результате специально спланированных кинетических экспериментов. Применяются два метода проведения кинетических экспериментов: дифференциальный и интегральный.

Интегральный метод заключается в изучении изменения состава реакционной смеси во времени при использовании реактора периодического действия или по длине при использовании проточного трубчатого или колонного аппарата. При этом измеряемые величины являются по существу интегральными величинами по отношению к скоростям превращений реагентов, поэтому этот метод и называется интегральным.

Схема интегрального реактора приведена на рис.4.2.1

Рис. 4.2.1. Схема интегрального реактора периодического

действия (а) и непрерывного (б) действия.

Рис.4.2.2.а) Изменение степени превращения во времени в интегральном реакторе (T2>T1).

Рис.4.2.2.б) Изменение степени конверсии по относительной длине реактора,

(Т2>T1).

Дифференциальный метод является модификацией интегрального метода, реализуемого в проточном трубчатом реакторе. Если реакционная зона в трубке очень небольшая, тогда для трубки можно записать следующее уравнение:

(4.2.1)

где t=l/u-среднее время пребывания реакционной смеси в реакционной зоне,

l- длина реакционной зоны, м, u- линейная скорость движения реакционной смеси, м/сек, k- константа скорости химической реакции

В этом случае экспериментально замеряемой величиной является сама скорость химической реакции. Чем меньше величина реакционной зоны l, тем ближе замеряемая величина к скорости реакции. Однако в этом случае увеличивается влияние погрешности в определении разности концентраций с. Выходом из этого положения является использование проточного реактора идеального перемешивания в качестве экспериментального реактора дифференциального типа. Экспериментальные данные, полученные в реакторе дифференциального типа, позволяют в результате довольно простой математической обработки определить кинетические параметры. Пусть, например, в дифференциальном реакторе протекает реакция n-го порядка по реагенту А. Тогда

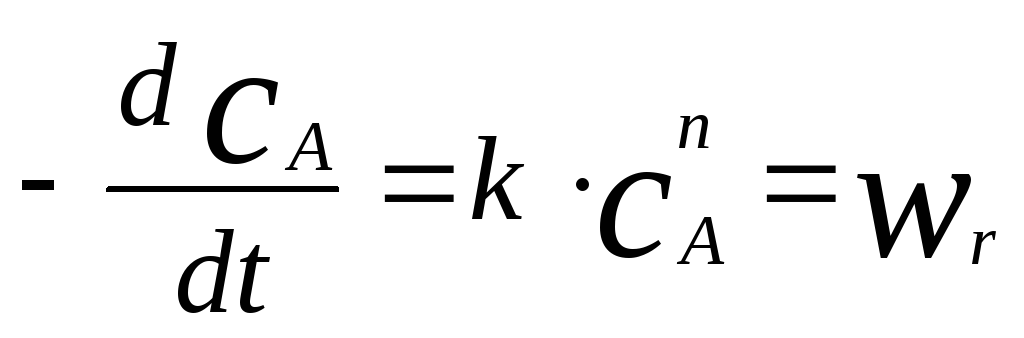
Определив экспериментально значение скоростей при различных концентрациях реагентов, получим набор данных вида:

(4.2.2)

Логарифмируя полученные экспериментальные данные (4.2.2), получим:

(4.2.3)

Откуда получаем:

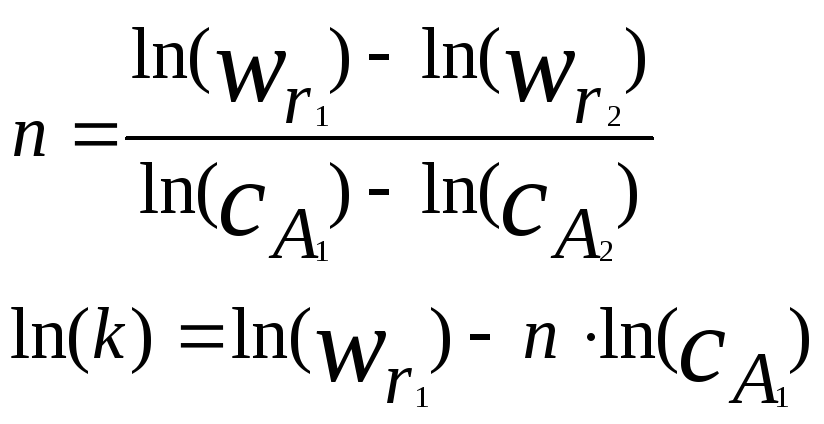
(4.2.4)

Значения n и k можно найти из графика, построенного в координатах , применяя в необходимых случаях метод наименьших квадратов.

Рис.4.2.3. Зависимость скорости реакции от концентрации компонентов в логарифмических координатах.

На рисунке 4.2.3. показаны результаты обработки кинетических данных, полученных в дифференциальном реакторе по методу наименьших квадратов. На графике приведены найденные значения кинетических параметров: порядок реакции n=1.075 и ln(k)=-. 1.1415. Здесь же приведен коэффициент корреляции, равный 0.9809, который свидетельствует о высокой степени корреляции и хорошем описании экспериментальных данных. Для определения предэкспоненциального множителя и энергии активации необходимо поставить эксперименты не только при различных концентрациях исходных реагентов, но и при различных температурах. В этом случае, при логарифмировании замеренных скоростей реакций, мы получим систему уравнений следующего вида:

(4.2.5)

где i- номер температуры, при которой проводились измерения.

Полученную систему уравнений можно решать методом наименьших квадратов как уравнение множественной регрессии.

Для сравнительно простых реакционных схем можно найти ln(k(T_i)) в сериях опытов при различных постоянных температурах. Затем можно использовать уравнение Аррениуса для определения предэкспоненциального множителя и энергии активации, используя метод наименьших квадратов. На рис.4.2.4 представлена процедура определения кинетических параметров – ln(k₀) и E из серии изотермических опытов.

Рис.4.2.4. Температурная зависимость константы скорости в соответствии с уравнением Аррениуса.

Из полученного линейного уравнения следует, что ln(k₀)=23.198, а энергия активации равна E=7162.2*R=7162.2*0.008314=59.54653 кДж/моль.

Процедура обработки экспериментальных данных, полученных в дифференциальном реакторе, довольно проста, применение метода наименьших квадратов позволяет вычислить также коэффициент корреляции и доверительные интервалы полученных кинетических параметров.

В принципе, такую же процедуру определения кинетических констант можно использовать и для обработки экспериментальных данных, полученных в интегральном реакторе, если полученные в интегральном реакторе кривые подвергнуть численному или графическому дифференцированию. Однако, такой метод обработки интегральных данных не получил распространения по двум причинам.

• Экспериментальные кривые обычно имеют ограниченное число точек по времени, что не позволяет использовать точные методы вычисления производных.

• Численное дифференцирование приводит к гораздо большему накоплению ошибок, чем численное интегрирование.

Поэтому для обработки кинетических кривых, полученных в интегральном реакторе, используют два основных приема.

1. Вычисление констант скорости из их выражения через время и концентрацию, которые могут быть получены путем интегрирования дифференциальных кинетических уравнений.

2. Поиск кинетических констант путем минимизации функции рассогласования между экспериментальными данными и расчетными, получаемыми при численном интегрировании дифференциальных уравнений скорости.

Рассмотрим применение первого метода на примере простой реакции первого порядка протекающей по схеме:

Запишем дифференциальное уравнение скорости этой реакции и его решение в следующем виде:

(4.2.6)

Постоянную интегрирования определим из начальных условий:

При. Отсюда . После этого окончательно получаем решение в виде:

(4.1.7)

Из уравнения (4.2.7) видно, что является линейной функцией времени, причем прямая линия выходит из начала координат

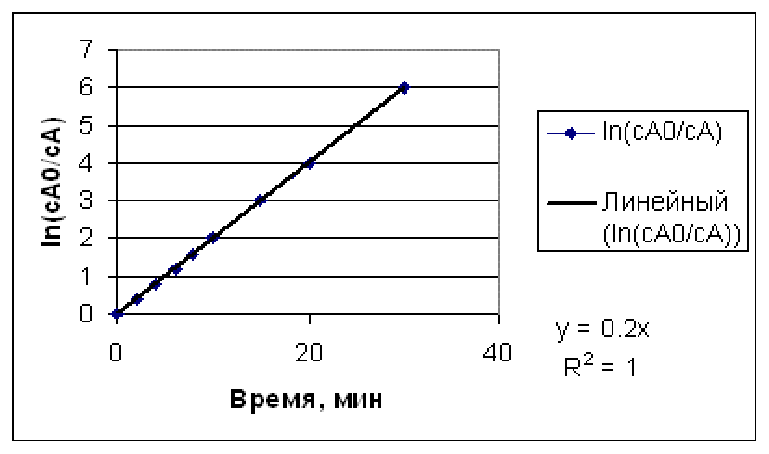
Рис.4.2.5. Определение константы скорости для реакции первого порядка по экспериментальным данным, полученным в интегральном реакторе.

. Построив график экспериментальных данных в указанной системе координат, мы получим график, приведенный в нижней части рисунка 4.2.5.

Рассмотрим теперь необратимую реакцию 2-го, протекающую в интегральном реакторе. Схема реакции может быть записана следующим образом:

(4.2.8)

Уравнение скорости, выраженное через скорость изменения концентрации конечного продукта, имеет вид:

(4.2.9)

где и– начальные концентрации исходных продуктов;– текущая концентрация продукта реакции. Уравнение (4.2.9) есть обыкновенное дифференциальное уравнение с разделяющимися переменными. После разделения переменных оно принимает вид:

(4.2.9а)

Решение этого уравнения дает следующее выражение для константы скорости.

Откуда получим выражение для константы скорости в виде:

(4.2.12)

Так как логарифм представляет собой безразмерную величину, то размерность константы скорости определяется размерностью сомножителя, стоящего перед логарифмом.

Рассмотрим исходное дифференциальное уравнение для реакции n-го порядка:

(4.2.13)

После разделения переменных получим это уравнение в полных дифференциалах в следующем виде:

Решение этого уравнения дает следующее выражение.

(4.2.16)

Для уравнения 2-го порядка, при n=2, уравнение приобретает вид:

(4.2.17)

Из уравнения (4.2.17) видно, что в координатах это уравнение является уравнением прямой линии с тангенсом угла наклона, равным константе скорости реакции. На рис.4.2.6 показана процедура определения константы скорости 2-го порядка при эквимолярном соотношении исходных компонентов.

Рис. 4.2.6. Определение константы скорости реакции 2-го порядка

при эквимолярном соотношении реагентов. k=tg().