
Учебное пособие по ТСиСА
.pdf
10
0 1 1 1 1 0 0 0 1 1
1 0 0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 1 1 0 0 0
0 1 0 0 1 0 1 1 0 0
0 1 0 0 1 1 0 1 0 0
0 0 0 0 0 1 1 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
0 1 1 1 1 0 0 0 1 1
1 0 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 1 0 0 0
0 1 0 0 0 1 0 1 0 0
0 0 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0
Рис. П2.4. Файл исходных данных для структурного анализа системы
Показанный на рис.П2.4 файл исходных данных, можно создать в любом текстовом редакторе. Кроме того, исходные данные можно также ввести непосредственно с клавиатуры, используя диалоговое окно, показанное на рис.П2.5.
Рис. П2.5. Диалоговое окно ввода исходных данных
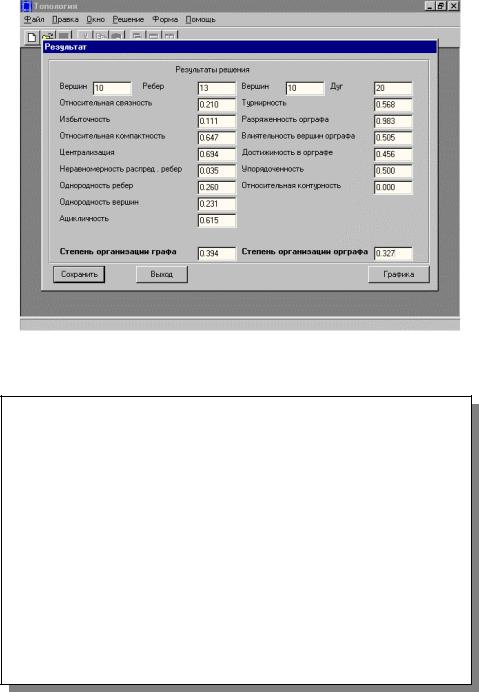
Результаты вычислений отображаются в диалоговом окне (рис.П2.6), а также сохраняются в выходном файле, который для структуры, граф и орграф которой показаны на рис.П2.1 и П2.2 соответственно, представлен на рис.П2.7.
Рис.П2.6. Форма результатов решения
Вершин______________________________10
Ребер_______________________________ 13
Относительная связность_____________ 0.210
Избыточность________________________ 0.111
Относительная компактность__________ 0.647
Централизация_______________________ 0.694
Неравномерность распределения ребер_ |
0.035 |
Однородность ребер__________________ |
0.260 |
Однородность вершин_________________ 0.231 Ацикличность________________________ 0.615
Степень организации графа___________ 0.394
Вершин______________________________10
Дуг_________________________________ 20 Турнирность_________________________ 0.568
Разряженность орграфа_______________ |
0.983 |
Влиятельность вершин орграфа________ |
0.505 |
Достижимость в орграфе______________ |
0.456 |
Упорядоченность вершин______________ 0.500
Относительная контурность___________ |
0.000 |
Степень организации орграфа_________ |
0.327 |
Рис.П2.7. Выходной файл результатов
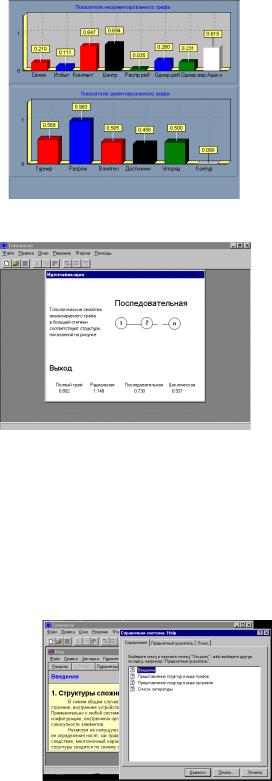
Результаты расчетов можно представить графически (рис.П2.8), а также решить задачу идентификации структуры
(рис.П2.9).
Рис. П2.8. Графическое представление результатов
Рис. П2.9. Идентификация анализируемой структуры
РПК «Топология» имеет встроенную систему помощи, позволяющую оперативно решать возникающие вопросы, связанные с терминологией графоаналитического моделирования структур и пониманием ее основных положений (рис.П2.10).
Рис. П.2.10. Справочная система РПК
ПРИЛОЖЕНИЕ 3
ПРИМЕРЫ ПРАКТИЧЕСКОГО ПРИМЕНЕНИЯ СТРУКТУРНОГО АНАЛИЗА СИСТЕМ
1. ИССЛЕДОВАНИЕ МНОЖЕСТВА ПАРЕТО
Нахождение множества Парето является полностью формализованным способом многокритериального выбора наиболее предпочтительного варианта из имеющегося множества и состоит в отказе от выделения единственной «наилучшей» альтернативы
исоглашении о том, что предпочтение одной альтернативе перед другой можно отдать, если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются. Принятые альтернативы образуют множество Парето
ивыбор на этом, как правило, заканчивается. При необходимости же выбора единственной альтернативы, наиболее часто множество Парето представляют в виде метрического пространства. Иными словами, в указанном множестве вводят одну из известных метрик, призванную обеспечить «измерение» расстояний либо от начала координат до альтернатив (точек пространства), либо от альтернатив до «идеальной» точки пространства и т.п.
Способам формирования метрик в научной литературе уделено огромное внимание. Всесторонне исследованы евклидова метрика, квадратичная и манхеттоновская метрики, метрики Брей-Картиса, Канберры и многие другие. Детальнейший анализ свойств большинства метрик позволил сделать вывод о невозможности их использования в произвольном пространстве или, например, в случае коррелированности характеристик альтернатив. Последнее обстоятельство обусловило необходимость создания декорреляционных метрик, таких, как нормализованная корреляционная метрика или метрика Махаланобиса. Однако и они не решили полностью проблемы метризуемости пространства альтернатив, т.к. в основе любой метрики лежит идея абсолютности (линейности) расстояния между двумя точками пространства.
Известно, что обобщающим понятием по отношению к любому метрическому пространству (а, следовательно, и к его метрике) является понятие топологического пространства (топологии по отношению к метрике), в котором в расстояние не вложен абсолютный смысл. Близость двух точек в топологическом пространстве определяется по результатам анализа окрестностей каждой его точки. Возникающие при этом очевидные преимущества топологического пространства перед любым метрическим пространством целесообразно использовать для исследования множества Парето, наделив его соответствующей топологией.
Для обеспечения общности дальнейших рассуждений допустим, что известен механизм порождения множества альтерна-
тив, на котором предстоит осуществлять выбор; определены цели (критерии), ради которых (в соответствии с которыми) производится выбор; множество Парето сформировано в соответствии с заданным алгоритмом его определения.
|
Следовательно, имеется множество альтернатив |
||
|
|
X = {xi}; |
( 1 ) |
|
|
xi = (ξi1, ξi2, …, |
ξik); i=1,…,n, |
где |
xi |
- альтернативы (точки пространства); |
|
|
n=card(X) |
- мощность множества Х; |
|
|
ξik |
- нормированное значение k-й характеристики |
|
|
|
i-й альтернативы; |
|
k - число характеристик каждой альтернативы. На множестве X можно естественным образом ввести топо-
логию τl по эквивалентности ξl (l = 1,…,k). В данном случае топо-
логическое пространство (X, τl) будет представлять собой полный граф G(X), информативность которого крайне низка вследствие того, что каждая альтернатива xi обладает каждой характеристи-
кой ξl. Однако если на графе Gl(X) ввести отношение доминиро-
вания по критерию ξl, которое антирефлексивно и асимметрично,
то граф Gl(X) трансформируется в ориентированный граф Gl→(X).
Очевидно, что в случае равенства характеристик ξi1 = ξj2 альтернатив xi и xj ребро графа Gl(X) ориентируется, как в направлении xi, так и в направлении xj.
Таким образом, имеется орграф Gl→(X) с кратностью дуг не более 2, который является исходным для всестороннего анализа альтернатив по критерию ξl. Для проведения такого анализа необходимо проследить содержательную связь между топологиче-
ским пространством (X, τ) и графом G(X).
Зафиксировав единичную окрестность, как шаблон для определения «удаленности» точек друг от друга, появляется возможность упорядочения элементов множества Парето с исполь-
зованием отображения d:X × X→N, сопоставляющим каждой паре натуральное число из N (множества натуральных чи-
сел). При этом отображение d является метрикой связного графового пространства G(X).
Обобщая сказанное, можно заключить, что любому тополо-
гическому пространству (X,τ), в котором X является окрестностью каждой своей точки, соответствует, по крайней мере, один связный (возможно бесконечный) граф. Вместе с тем, очевидно, что в случае существования множества Парето данный граф не только связный, но и полный, вследствие эквивалентности по наличию всех характеристик у всех элементов множества.
Для ориентированного графа G→(X), полученного в резуль-
тате задания на графе G(X) отношения доминирования ξ, также справедливы все приведенные выше рассуждения за исключени-
ем того, что метрика d→, также наследуемая от τ, учитывает ориентированность дуг орграфа.

Для упорядочения альтернатив по критерию ξl с использо-
ванием орграфа Gl→(X) наиболее целесообразно воспользоваться одним из его инвариантов, а именно показателем вершинной достижимости. Данный показатель отражает насколько «быстро» можно из вершины i «попасть» (достигнуть) в вершину j (вершины j). Физически это соответствует тому, насколько альтернати-
вы «удалены» по предпочтительности (по критерию ξ) друг от друга. Поэтому определив минимальные пути для каждой вершины орграфа, для каждого элемента множества Парето можно рассчитать:
b |
= b э λ ; |
|
|
|
|
|
|
|
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n R |
= n − 1; |
|
|
|
1, при ∑ dij |
|
||||||
|
|
|
|
|
j =1 |
|
|
|
|
|
|
|
|
|
n R |
|
|
|
n − 1 |
|
∑ dij > n − 1; |
|
||||
biэ = |
|
|
, |
при |
( 2) |
|||
n |
R |
|||||||
|
|
∑ dij |
|
j =1 |
|
|
||
|
|
|
|
|
||||
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
R |
|
|
|
|
|
|
∑ dij |
|
n R |
|
|
|||
|
|
j =1 |
|
|
|
|
|
|
|
|
|
, |
при |
∑ dij |
< n − 1, |
|
|
|
|
|
|
|||||
|
n − 1 |
|
j =1 |
|
|
|||
|
|
|
|
|
|
|
|
|
λ = 1 − nнi − 1 , i = 1, n, |
|
i |
n − 1 |
|
|
где d ij - элемент матрицы минимальных путей D ; nнi - количество нулей в i-й строке матрицы D .
Отметим, что при biэ =n-1 из i-й вершины выходят дуги ко всем остальным вершинам. Это означает полное доминирование альтернативы xi над всеми остальными. При
|
|
|
n |
R |
|
|
n − 1 |
|
∑ d ij |
||
b э = |
или b э = |
j=1 |
|
возможны и длинные пути и отсутствие |
|
|
|
|
|||
i |
n R |
i n − 1 |
|||
|
∑ d ij |
|
|
|
|
j=1
таковых вообще. Коэффициент λi учитывает возможность прин-
ципиальной достижимости вершин из вершины i, т.е. общую возможность по доминированию альтернативы xi над остальными.
Очевидно, что показатель b должен быть определен для ка-
ждого элемента множества Парето по всем критериям ξl (l=1,…,k) . В результате этого получается новое пространство XГ с системой координат B=(b1, b2,…, b k) и точками пространства ik). Механизм получения данного пространства
схематично показан на рис.П3.1.
Целесообразно рассмотреть структуру пространства XГ. Во-первых, данное пространство имеет абстрактную точку
отсчета x0=(0, 0,…, 0) .
Во-вторых, B [0, 1], т.е. каждая координата пространства отображается в интервал [0, 1].
G1→(X)
xi=½½dij→½½
X
Г
G2→(X)
xi=(ξi1, ξi2,…, ξik) |
xiГ=(bi1, bi2, …, b ik) |
|
xi=½½dij→½½ |
Gk→(X)
…
Рис. П3.1. Последовательность построения пространства XГ
Наконец, в-третьих, нетрудно показать, что XГ гомеоморф-
ное каждому Gl→(X) (l=1,…, k) . Так, существует отображение f: Gl→(X)→ XГ, которое является сюрьективным и инъективным одновременно, т.е. биективным. Кроме того, отображение f непре-
рывно, как непрерывно и f –1 . Следовательно, пространства Gl→(X) и XГ топологически эквивалентны. Из этого следует важнейший вывод о том, что d→→ρ, где ρ - метрика пространства XГ. При этом данное пространство является евклидовым, т.к. удовлетво-
ряет известным аксиомам этого пространства и, следовательно, ρ - евклидова метрика.
Таким образом, осуществив переход от произвольного пространства X к евклидову пространству XГ появилась объективная возможность использовать евклидову метрику для сравнения альтернатив, включенных в множество Парето. Выражение для определения ρ в этом случае будет иметь вид:
