Учебное пособие по ТСиСА

Гомогенность - это свойство структуры, характеризующее топологическую однородность системы множеств ее элементов и связей.

Гомогенные структуры содержат однородные элементы и связи. Это означает топологическую тождественность положений элементов и связей в структуре, определяемых характером заданной системы инцидентности в графе.

Плотность - это свойство структуры, заключающееся в топологической близости ее элементов.

Близость двух элементов, в данном случае, понимается как длина минимальной связывающей их цепи графа.

Радиальность - это свойство структуры, характеризующее наличие и выраженность ее топологического центра.

Топологический центр может представлять собой либо конкретный элемент, либо группу элементов, и тогда имеет место топологическое ядро структуры (клика графа), либо и то и другое, что позволяет выделить элемент (группу элементов) как важнейший (центральный) из имеющегося множества.

Перечисленные свойства являются необходимыми для всесторонней характеристики организации структуры. Однако их следует рассматривать как свойства, интенсивность проявления которых зависит от первичных (элементарных) топологических свойств. В этом случае множество первичных топологических свойств есть достаточное множество, элементы которого содержат всю необходимую информацию для описания и оценки орга-

низации структуры. Как показано на рис.4.1, к таким свойствам относятся:

для целостности - связность (существование простой цепи между любой парой вершин графа) и избыточность (превышение числа ребер в графе над минимально необходимым для обеспечения связности);

для гомогенности - однородность элементов структуры (топологическая тождественность положений вершин графа) и однородность связей структуры (топологическая тождественность положений ребер графа);

для плотности - компактность (обобщенная характеристика минимальных цепей графа) и цикломатичность (наличие и расположение независимых циклов графа);

для радиальности - централизация (существование топологического центра) и ацикличность (характеристика системы инцидентности графа, при которой невозможно задание хотя бы одной замкнутой цепи).

Наличие, а также уровень проявления перечисленных топологических свойств структуры определяют ее внутреннюю упорядоченность и организацию, что обуславливает необходимость их анализа и количественной оценки для математического описания топологического облика структуры.

4.2. Показатели топологических свойств структур-графов

Основная идея, которая заложена в систему показателей топологических свойств - изоморфизм графов, формализующих (представляющих) одну и ту же структуру. Поэтому все показатели топологических свойств следует рассматривать как инварианты графов. Кроме того, в соответствии с общесистемными требованиями, предъявляемыми к показателям любых свойств, они, безусловно, аналитические; выражаются в количественной шкале и допускают объективное их вычисление, а также чувствительны к изменению оцениваемых свойств.

Известно, что графу, как математическому объекту, можно поставить в соответствие его аналитическое представление, например, матричное. Основными матрицами графа, содержащего n вершин и m ребер, являются:

матрица смежности вершин Α, в которой элемент aij = 1 (i = 1, n, j = 1, n) свидетельствует о наличии ребра между i-ой и j-ой вершинами, причем, в соответствии с принципом метризуемости топологического пространства, при i=j всегда aij = 0;

матрица инциденций, в которой строки соответствуют вершинам, столбцы - ребрам, а элемент матрицы, стоящий на пересечении i-ой строки и j-го столбца, равный 1, указывает на их инцидентность.

В теории графов показано, что эти матрицы несут в себе всю информацию, содержащуюся в графе и могут быть использованы

для построения производных от них матриц, таких как матрица цепей, матрица минимальных цепей, матрица достижимости и др.

Важнейшее топологическое свойство, которое, вообще говоря, обуславливает наличие всех остальных свойств - связность графа. Как отмечалось, связность означает существование цепи между каждой парой вершин графа. При этом под цепью понимается такая последовательность вершин и ребер, в которой все ребра различны.

Оценка связности графа в такой постановке носит абсолютный характер, т.е. показатель связности должен отвечать на вопрос: связен ли граф или нет (метризуемо ли топологическое пространство или нет). Поэтому коэффициент абсолютной связности Ra = 1 означает выполнение условия связности, а Ra = 0 , со-

ответственно, не выполнение.

Наиболее удобно абсолютную связность графа определять с

использованием матрицы минимальных цепей D. Матрица D = d ij

формируется на основе матрицы A следующим образом.

Матрица A = aij (i = 1, n, j = 1, n) может рассматриваться как

(включающих два ребра) между каждой парой вершин графа. В этом случае, если aij(1) = 0, а aij(2) ¹ 0, то в матрицу минимальных цепей D графа в i-ю строку и j-й столбец запишется 2. Очевидно,

что максимально возможная степень матрицы A составляет (n-1).

Откуда max{d ij } = (n − 1) , где d ij - элемент матрицы D. Нетрудно за-

метить, что элементы d ij при i=j не несут, в данном случае,

сколько-нибудь существенной информации. Поэтому при i=j целесообразно положить d ij = 0 . Однако при i ¹ j и d ij = 0 , между вер-

шинами i и j отсутствует минимальная цепь (да и любая цепь вообще), т.е. если в матрице D количество нулевых элементов превышает n , то граф, по которому построена эта матрица - не связен и, следовательно, Ra = 0 .

Заметим, что в связном графе с n вершинами должно быть, по крайней мере, (n-1) ребер. Это условие непосредственно вытекает из определений - аксиом, приведенных выше, так как смежность двух вершин графа отождествляется с их принадлежностью своим единичным окрестностям. В этом случае, если d ij = 1, тщ между i-й и j-й вершинами существует ребро (причем единственное).

Рассматривая приложение теории графов к анализу структур систем, в некоторых источниках сформулированное условие считается не только необходимым, но и достаточным. Однако допустим, что граф G содержит n вершин, которые произвольно разбиты на два непересекающихся подмножества X 1 и X 2 с количест-

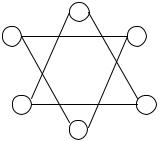
Рис. 4.2. Граф Давида

Если граф связен абсолютно (о чем свидетельствует коэффициент абсолютной связности), то коэффициент относительной связности должен показать «силу» связности, соизмеряя ее с «силой» связности в графе, содержащим такое же количество вершин, но обладающим максимальной связностью. Известно, что таким графом является полный граф, в котором каждая пара вершин смежена. С учетом этого, выражение для коэффициента относительной связности графа запишется в следующем виде:

Сmin = 1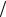(n − 1) - для структур (например, последовательных), имею-

щих минимальную относительную связность, т.к. удаление любого ребра в их графах ведет к потере абсолютной связности.

Кроме приведенного коэффициента, относительную связность можно оценить числом внутренней устойчивости вершин графа

где жестве.

При этом под внутренне устойчивым подмножеством вершин графа понимается множество, между вершинами которых нет соединяющих ребер.

Другим свойством структуры, в определенном смысле дополняющим свойство связности, является структурная избыточность. Показатель этого свойства оценивает превышение числа ребер в графе над числом, необходимым для обеспечения минимальной относительной связности:

Структурная избыточность может также характеризоваться абсолютной мощностью графа

или относительной

Необходимо отметить, что показатели связности и избыточности могут быть использованы для описания свойства более высокого уровня - целостности структуры.

В основе характеристики гомогенности структуры лежит оценка однородности некоторого множества X = {x1 , x2 , . .. , xn }. На множестве X предполагается заданным отношение эквивалентности. В соответствии с этим отношением данное множество разби-

t

вается на t классов эквивалентности X = U X i . Классы эквивалент-

i =1

ности задают состав множества X '= {n , n1 , . .. , nt } , где n и ni - мощно-

сти множеств X и X i соответственно. Коэффициент однородности множества X в этом случае можно рассматривать как вероятность случайного выбора из X двух одинаковых (эквивалентных) элементов, т.е.

При этом Kоэ изменяется в пределах 1 ≤ Kоэ ≤ 1 , поэтому при

n

заданных n и t

Согласно выражения (4.7), для любого действительного числа b > 0 Kоэ (n1b, n2 b, .. . , ntb ) = Kоэ (n1 , n2 , .. . , nt ). Это справедливо и для b = 1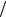d , где d > 1 есть наибольший общий делитель чисел n1 , n2 , ... , nt .

Поэтому можно говорить, что коэффициент однородности характеризует некоторое «ядро разнообразия» множества, представляющее собой минимальный по числу элементов состав, сохраняющий заданный удельный вес элементов

Для определения числа типов элементов t и количества элементов каждого типа ni , требуется определить ранг каждой вер-

шины графа. Данная характеристика позволяет распределить вершины в порядке их значимости, которая определяется здесь только числом ребер, связывающих какую-либо вершину с другими вершинами.

В общем виде наиболее точно ранг вершины, в данной постановке, определяется функцией вида

где d (i ) (k ) - количество цепей в графе длины k, идущих от элемента i, которые являются элементами матрицы смежности, возведенную в степень i=1...n.