Как строятся «экономические кривые»?

S = f(P)  предложение от цены P = f ^-1(S)

P = g(D) цена от спроса (P₀,Q₀) – точка равновесия

Эластичность спроса

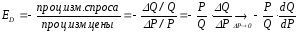
Пусть Q = CP^ПриE_D =  > 1 – спрос эластичен, при   1 - нет

Эластичность предложения. Пусть Q = CP^ПриE_S =  > 1 – предложение эластично, при   1 - нет

§9. Двойной интеграл.

f(x,y) = f(P)  C(G), G  R²  = ₁,₂,…,_n Площади подобластей _i , диаметры d_i P_i  _i, i = 1, 2,…,n 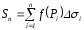max d_i  0 (1 i n)

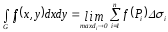
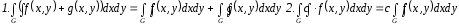
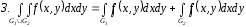повторных интегралов

G ограничена кривыми y = ₁(x) снизу, y = ₂(x) сверху и прямыми x = a слева, x = b справа, ₁C[a,b], ₂C[a,b], ₁(x) ₂(x)

Или: G ограничена кривыми х = ₁(у) слева, х = ₂(у) справа и прямыми у = с снизу, y = d сверху, ₁C[c,d], ₂C[c,d], ₁(y) ₂(y)

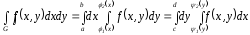Если граница задается несколькими формулами, вычисляют несколько интегралов. Изменить порядок интегрирования

Замена переменных. x = (u,v), y = (u,v) взаимно-однозначное непрерывно дифференцируемое отображение  Ouv  G Oxy u = (x,y), v = (x,y) G   якобиан

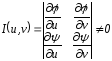
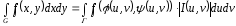
Для полярных координат

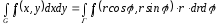
§10. Приложения двойных интегралов. Геометрические приложения

а) Площадь S плоской области G

в декартовых прямоугольных, в криволинейных, в частности, в полярных

б) Объем V, ограниченный сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z = 0 и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Оху область G

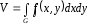
Если тело ограничено сверху непрерывной поверхностью z = f₁(x,y), снизу непрерывной поверхностью z = f₂(x,y), и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Оху область G

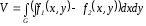
Механические приложения

Пластинка переменную поверхностную плотность  =  (х,у) масса М статические моменты М_х и М_у относительно осей Ох и Оу

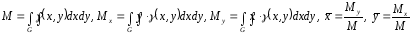
координаты центра масс

Моменты инерции пластинки относительно осей Ох и Оу

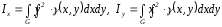
Глава 10. Дифференциальные уравнения.

§1. Уравнения 1-го порядка.

F(x,y,y) = 0 y = f(x,y) (1) (a,b) y = (x) (x) (x,y) = 0

y = (x,C) y = (х,C₀) (x,y,C) = 0

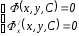
§2. Уравнения с разделяющимися переменными.

y = f(x,y) f(x,y) = f₁(x)f₂(y)

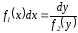
M(x,y)dx + N(x,y)dy = 0, M(x,y) = M₁(x) M₂(y), N(x,y) = N₁(x)N₂(y)

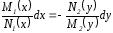
y = f(ax + by +d), b0 u(x) = ax + by(x) +d  u = a + b f(u)

§3. Однородные уравнения.

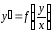M(x,y)dx + N(x,y)dy = 0 kR: M(tx,ty) = t^kM(x,y), N(tx,ty) = t^kN(x,y), t0

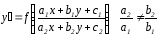к однород., « = »  к ур-ям с разд. перем.

§4. Линейные уравнения 1-го порядка.

y = P(x)^.y + Q(x) Q(x)0  y = P(x)^.y

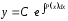
1) Метод вариации произвольной постоянной (Лагранжа)

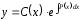
2) Метод подстановки y(x) = u(x)^.v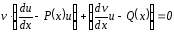(x)  u = u₁(x), v = v(x,C)  y(x)

§5. Уравнение Бернулли.

y = P(x)^.y + Q(x)^.y^m m0, m1

1) Подстановка z = y^1-m m>1 y = 0

2) Метод подстановки y(x) = u(x)^.v(x) 

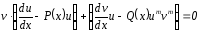
u = u₁(x), v = v(x,C)  y(x)

§6. Теорема существования и единственности решения.

Задача Коши для уравнения y = f(x,y) начальному условию у(х₀) = у₀

Теорема 1. (Коши) D Oxy f_y(x,y) (x₀,y₀)D x₀ – h < x < x₀ + h

Особое решение y = (x,C)

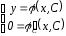
§7. Дифференциальные уравнения высших порядков.

F(x,y,y,y,…,y⁽ⁿ⁾) = 0 y⁽ⁿ⁾ = f(x,y,y,…,y^(n-1)) (2)

Начальные условия y(x₀) = y₀, y(x₀) = y₁,…, y^(n-1)(x₀) = y_n-1 (3)

y =  (x,C₁, C₂,…,C_n)

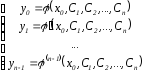
Теорема 2 (существования и единственности решения задачи Коши)

(2) f(x,y,y,…,y^(n-1)) D 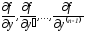(x₀,y₀,y₁,…,y_n-1)D x₀  h < x < x₀ +h

§8. Уравнения, допускающие понижение порядка.

а) y⁽ⁿ⁾ = f(x) y = dxdx…f(x)dx + P_n-1(x)

б) F(x, y^(k),…,y⁽ⁿ⁾) = 0 y^(k) = z(x)

в) F(y, y,…,y⁽ⁿ⁾) = 0 y = p(y) 

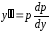
г)

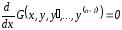
§9. Линейные однородные уравнения.

y⁽ⁿ⁾ + a₁(x)y^(n-1) + … + a_n-1(x)y + a_n(x)y = 0 (4)

y₁(x) y(x) = y₁(x)z(x) (n1)-го порядка

Теорема 3 система функций у₁(х), у₂(х), … , у_n(х) (4) определитель Вронского

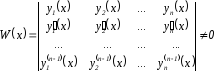
Общее решение (4) y₀(x) = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) фундаментальной

§10. Линейные неоднородные уравнения.

y⁽ⁿ⁾ + a₁(x)y^(n-1) + … + a_n-1(x)y + a_n(x)y = f(x) (f(x)  0) (5)

y(x) = y₀(x) + y_(x) y₀(x)- общее решение (4) y_(x) - частное решение (5)

Если известны у₁(х), у₂(х), … , у_n(х), то можно найти y_(x) методом Лагранжа вариации произвольных постоянных.

В частности, для уравнения 2-го порядка y + a₁(x)y + a₂(x)y = f(x) (6)

сначала решают однородное уравнение y + a₁(x)y + a₂(x)y = 0,

получают фундаментальную систему у₁(х), у₂(х) и общее решение y₀(x) = C₁y₁(x) + C₂y₂(x),

затем по методу Лагранжа общее решение (6) ищут в виде y(x) = C₁(x)y₁(x) + C₂(x)y₂(x),

где C₁(x)иC₂(x) находят из системы

, после чего интегрированием находятC₁(x)иC₂(x)