
- •Глава 1. Линейные системы и матрицы.
- •§2. Системы линейных уравнений.
- •Элементарные преобразования строк матрицы:
- •§3. Метод Гаусса. Метод Жордана.
- •§4. Действия над матрицами.
- •§5. Обратная матрица.
- •§6. Балансовая модель.
- •§7. Свойства определителей.
- •§8. Формулы Крамера.
- •Глава 3. Функции. Пределы. Непрерывность.
- •§1. Множества. Логическая символика.
- •§2. Функции вещественной переменной.
- •§3. Предел последовательности вещественных чисел.
- •§3. Предел последовательности вещественных чисел.
- •§4. Предел функции.
- •Глава 4. Дифференцирование функций одной переменной.
- •§1. Определение производной.
- •§2. Правила дифференцирования.
- •§7. Раскрытие неопределенностей. Правила Лопиталя.
- •§8. Формула Тейлора.
- •§5. Непрерывные функции. Теоремы Коши и Вейерштрасса.
- •§6. Вычисление пределов. Практические советы.
- •При X предел отношения степенных функций зависит от старших степеней, приx 0 от младших.
- •Глава 5. Исследование функций и построение графиков.
- •§1. Возрастание и убывание функции. Экстремум.
- •Достаточное условие экстремума.
- •§2. Направление выпуклости. Точки перегиба.
- •Достаточное условие перегиба.
- •§3. Асимптоты.
- •§4. Общий порядок построения графика.
- •§5. Численное решение уравнений. Метод Ньютона.
- •Глава 6. Комплексные числа.
- •§1. Действия над комплексными числами.
- •§2. Геометрическая интерпретация комплексных чисел.
- •§3. Формулы Эйлера и Муавра.
- •При делении …
- •§4. Извлечение корня из комплексного числа.
- •§5. Решение алгебраических уравнений.
- •Глава 7. Вычисление неопределенных интегралов.
- •Как строятся «экономические кривые»?
- •§9. Двойной интеграл.
- •§10. Приложения двойных интегралов. Геометрические приложения
- •Механические приложения
- •§11. Линейные однородные уравнения с постоянными коэффициентами.
- •§12. Линейные неоднородные уравнения с постоянными коэффициентами.
- •§13. Понятие системы дифференциальных уравнений.
§11. Линейные однородные уравнения с постоянными коэффициентами.
Общий вид y(n) + a1y(n-1) + … + an-1y + any = 0(7)
Характеристическое уравнение n + a1n-1 + … + an-1 + an = 0 (8)
веществ. корням кратностиr уравнения (8)rлин. незав. решений (7)ex, x ex, … , xr-1 ex
паре компл. = iкратностиs уравнения (8)sпар лин. незав. решений (7)
excos x, xexcos x, … , xs-1excos x; exsin x, xexsin x, … , xs-1exsin x
§12. Линейные неоднородные уравнения с постоянными коэффициентами.
Общий вид y(n) + a1y(n-1) + … + an-1y + any = f(x)(9)
y(x) = y0(x) + y(x) y0(x)- общее решение (7) y(x) - частное решение (9)
Специальные виды f(x) в уравнении (9):
f(x) = ( d0xm + d1xm-1 + … + dm)ekx
f(x) = [(a0xk + a1xk-1 + … + ak)cos qx + ( b1xl + b2xl-1 + … + bl)sin qx]epx
метод неопределенных коэффициентов
а) kиp iqне корни (8)yищется в виде
y = ( D0xm + D1xm-1 + … + Dm)ekx
y = [(A0xM + A1xM-1 + … + AM)cos qx + ( B1xM + B2xM-1 + … + BM)sin qx]epx, M = max( k, l )
б) kилиp iqсовпадают с корнем (8) кратностиryищется в виде
y =xr ( D0xm + D1xm-1 + … + Dm)ekx
y =xr [(A0xM + A1xM-1 + … + AM)cos qx + ( B1xM + B2xM-1 + … + BM)sin qx]epx, M = max( k, l )
§13. Понятие системы дифференциальных уравнений.
kуравненийxиkфункцийy1(x),
y2(x),
… , yk(x)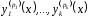
 каноническая,n
= p1 + p2
+ … + pkпорядок системы
каноническая,n
= p1 + p2
+ … + pkпорядок системы
p1 = p2 = … = pk= 1 нормальная система
Решение на (a,b)y1 = 1(x), y2 = 2(x), … , yk = k(x)
y(n) = f(x,y,y,…,y(n-1)) (2)
Глава 12. Комбинаторика.
Сколькими способами можно выбрать n элементов из k?
§1. Размещения.
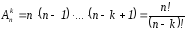 число размещений
из n
элементов по k
число размещений
из n
элементов по k
§2. Перестановки.
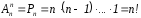 число перестановок
из n
элементов. 0!
= 1.
число перестановок
из n
элементов. 0!
= 1.
§3. Сочетания.
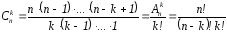 число сочетаний
из n
элементов по k
число сочетаний
из n
элементов по k
Порядок выбора элементов не важен
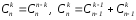 рекуррентное
соотношение. Треугольник Паскаля.
рекуррентное
соотношение. Треугольник Паскаля.
 бином (Ньютона)
бином (Ньютона)
Биномиальные коэффициенты

§4. Размещения и сочетания с повторениями.
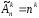 число
размещений с повторениями из n
элементов по k
число
размещений с повторениями из n
элементов по k
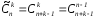 число сочетаний
с повторениями из n
элементов по k
число сочетаний
с повторениями из n
элементов по k
§5. Перестановки с повторениями.
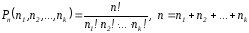
Глава 11. Ряды.
§1. Сумма ряда. Сходимость ряда.
 u1
+ u2
+ … + un
+ … (1) числовой
ряд. un
- общий
член ряда
u1
+ u2
+ … + un
+ … (1) числовой
ряд. un
- общий
член ряда
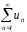 (1)
(1)
n – я частичная сумма ряда (1) Sn = u1 + u2 + … + un unSn
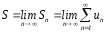 сходится
расходится
сходится
расходится
§2. Свойства сходящихся рядов.
Т.1 (1) сходится = S cu1 + cu2 + … + cun + … = (cun) сходится = cS
Т.2 un vn Su, Sv (un + vn) , (un – vn) Su + Sv Su Sv
Т.3 «Сходимость ряда определяется его «хвостом» »
§3. Необходимый признак сходимости ряда.
Т.4 un сх. un 0 при n
Гармонический
ряд
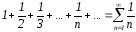 расходится ( =
)
расходится ( =
)
§4. Сравнение рядов.
Т.5 а) n un 0 б) n un vn в) vn сх. un сходится
Т.6
(предельный признак сравнения) n
un
0, vn
0
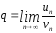 ,0 < q
< +
un
vn
,0 < q
< +
un
vn
§5. Признак Даламбера.
Т.7
un
(1) , un
0,
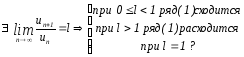
§6. Признак Коши (радикальный).
Т.8
un
(1) , un
0,
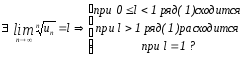
Формула
Стирлинга
 ,0 <
< 1
,0 <
< 1
§7. Интегральный признак.
Т.9
f(x)
> 0, монотонна
при x
1 nN
f(n)
= un
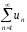 (1) сх. одновременно с
(1) сх. одновременно с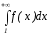
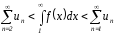 (р)
= n-p
при p>1
сх., при p1
расх.
(р)
= n-p
при p>1
сх., при p1
расх.
§8. Знакочередующиеся ряды. Теорема Лейбница.
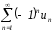 ,
un
0 (2)
,
un
0 (2)
Т10.
u1
u2…
un
un+1…
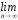 un=
0
(2) сх.
u1
un=
0
(2) сх.
u1
Следствие. Для (2) Sn S un+1
§9. Знакопеременные ряды. Абсолютная и условная сходимость.
Т.11.
(1)
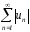 (3)
сх.
(1) тоже сх. ( Если ряд абсолютно
сходится,
то он сходится)
(3)
сх.
(1) тоже сх. ( Если ряд абсолютно
сходится,
то он сходится)
Условно сходящийся – сходится, но не абсолютно.
Достаточные признаки для знакопеременных рядов
Даламбера
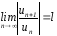 ,
радикальный Коши
,
радикальный Коши 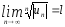 ,
интегральный f(n)
= un
,
интегральный f(n)
= un
Т.12. Если ряд абс. сходится, то он остается абс. сходящимся при любой перестановке его членов.
Т.13. Если ряд сх. условно, то А можно так переставить члены этого ряда, что его сумма будет =А.
§10. Понятие о функциональном ряде.
fn(x),
nN
D
f1(x)
+ f2(x)
+ … + fn(x)
+… =
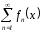 (4)x0D
xD1D
(4)x0D
xD1D
По
признакам Даламбера и Коши

абсолютная сходимость (4) при l(x)<1, расходимость при l(x)>1
§11. Степенные ряды. Теорема Абеля.
a0 + a1(x – x0) +a2(x – x0)2+…+an(x – x0)n+… = an(x – x0)n (5) x – x0
a0 + a1x +a2x2+…+anxn+… = anxn (6)
T.14. (6) сх. при x00 абс. сх. при x: x<x0 (6) расх. при x = x1 расх. при x: x>x1
Радиус
сходимости R
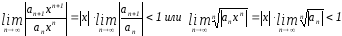
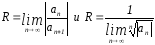
§12. Дифференцирование и интегрирование степенных рядов.
Т.15. x – x0<R (5) – непрерывная функция
Т.16. x – x0<R (5) можно дифференцировать
Т.17. x – x0<R (5) можно интегрировать по отрезку внутри x – x0<R от х0 до х
§13. Разложение функций в ряд Тейлора.
T.18.
f(x)
x
– x0<R
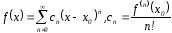
§14. Приложения степенных рядов.
А. Вычисление значений функций
Погрешность

Б. Интегрирование функций
В. Решение дифференциальных уравнений
§15. Понятие о рядах Фурье.
Тригонометрическая система функций 1,cos x, sin x, cos 2x, sin 2x, … , cos nx, sin nx, …
ортогональной на [-,]
Если
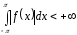 , то
, то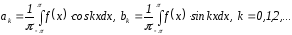 коэффициенты
коэффициенты
Фурье f(x)
Ряд
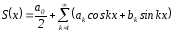 f(x)
четная bk=0
f(x)
нечетная
ak=0
f(x)
четная bk=0
f(x)
нечетная
ak=0
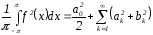
T.19. Если периодическая f(x) с периодом 2 имеет на [-,] конечное число точек разрыва 1 рода, то S(x) сходится к f(x) в каждой точке непрерывности и к ½[f(x+0)+f(x0)] в точках разрыва
