47

Власов м. П.

конспект лекций по дисциплине ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ В КОММЕРЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

Только себе и бесплатно

ТЕМА № 13

Дискретные задачи

для студентов всех форм обучения

Содержание

Стр.

1.Дискретная оптимизация .……………………………………………………. 2

2.Оптимальное управление дискретным объектом …….……………...…….. 9

3.Задача календарного планирования трудовых ресурсов ………..……….. 12

4. Задача о замене оборудования …………………………………………….. 15

5. Планирование емкости рынка на основе жизненного цикла ……….…… 19

6. Определение объема спроса на основе учета особенностей использования продукции с длительным циклом изготовления ………………………….… 25

7. Прогнозирование ассортимента спроса …………………………………... 33

Санкт-Петербург 2002-212

1. Дискретная оптимизация

Дискретная модель – математическая модель, переменные которой принимают дискретные значения (целочисленные, булевы и др.). К дискретным моделям приводят часто встречающиеся в экономике проблемы выбора из конечного множества альтернатив, особенно если это множество непосредственно не обозримо, так что модель обеспечивает не только оценку альтернатив, но и их синтез из более простых элементов. Дискретные модели изучаются дискретной математикой, в частности, дискретным программированием, теорией графов, комбинаторикой. Дискретные модели весьма разнообразны, общие методы их анализа и решения часто оказываются неэффективными, что обуславливает целесообразность разработки специальных методов, ориентированных на отдельные, подчас узкие классы этих моделей.

Дискретная оптимизация (дискретное программирование, комбинаторная оптимизация, целочисленное программирование) – часть математического программирования, в которой исследуются и решаются экстремальные задачи на целочисленных решетках и конечных множествах.

В терминах дискретной оптимизации формализуются многие важные задачи экономики, управления, планирования, техники, проектирования и военного дела. Например:

• задача размещения и специализации предприятий;

• задача оптимизации комплекса технических средств доставки грузов;

• некоторые задачи оптимального проектирования (оптимальный выбор проектов);

• оптимизация избыточности (надежности);

• оптимальное разбиение территории на зоны обслуживания;

• задача синтеза структур информационных связей в больших системах;

• задачи унификации и стандартизации;

• задача маршрутизации;

• задача обновления оборудования;

• задача распределения капиталовложений;

• задача типизации технических объектов;

• некоторые задачи планирования и управления научными исследованиями;

• задачи оптимизации учебных расписаний;

• задачи выбора структур (конфигураций) вычислительных систем;

• задача оптимизации синтеза шарнирно-стержневых конструкций;

• задача выбора оптимального портфеля акций;

• некоторые задачи оптимизации логического проектирования.

Среди прикладных задач, уже решавшихся и формализованных с помощью моделей дискретной оптимизации, можно назвать:

• задачи выбора очередности передач в спутниках связи;

• задачу долгосрочного развития морского газового месторождения;

• задачу обустройства нефтяных месторождений;

• задачу планирования ремонтов электростанций в рамках Единой энергетической системы;

• задачи оперативного планирования гибких автоматизированных производств;

• задача оптимальной комплектации блоков модулями;

• задача проектирования сетей связи;

• многоуровневые задачи складирования;

• задачи оптимального раскроя.

Источниками возникновения дискретности в оптимизационных задачах служат:

• физическая неделимость. Например, нельзя купить или сделать 0.5 кресла или станка;

• наличие альтернатив (вариантов). Например, если существует несколько возможных вариантов проекта строительства дома, завода, или несколько вариантов размещения объектов (складов, магазинов, заводов, электростанций), а может быть реализован только один из них;

• другие комбинаторные задачи (т.е. задачи на конечное множество).

Например, задача оптимизации на перестановках (размещение мебели в квартире или комнате), т.е. поиск такой перестановки чисел (), которая оптимизирует функцию

, (1.1.)

при условии

, (1.2.)

где - некоторое множество перестановок, например, множествовсех перестановок. Иначе говоря, множество допустимых решений либо совпадает со множеством всех перестановок- примером является задача выбора (назначения), либо является его собственным подмножеством – примером является задача о коммивояжере. Еще один пример комбинаторной задачи – задачи теории расписаний (задача календарного планирования).

Одна из наиболее важных задач дискретной оптимизации – задача целочисленного программирования, в которой ищется вектор , оптимизирующий функцию

(1.3.)

при условии

, , (1.4.)

, , (1.5.)

- целое, , (1.6.)

где , а каждый из символовможет обозначать либо знак равенства (), либо неравенства (). Все- положительные числа, а прикаждоеявляется еще и целым числом. Некоторые (или все)могут удовлетворять условию, что означает отсутствие верхнего ограничения на переменные. В важном частном случае,, переменнаяможет принимать только два значения: 0 или 1 (булева переменная).

При получается полностью целочисленная задача линейного программирования, при- частично целочисленная задача линейного программирования. Естественно считать, поскольку приполучается задача линейного программирования, не являющаяся задачей дискретной оптимизацией.

Рассмотрим в качестве примера задачу, в которой одновременно присутствуют многие ограничения, типичные для различных прикладных задач. Это вариантная задача специализации предприятий (вновь проектируемых или реконструируемых), которые должны выпускатьвидов продукциив количествах не меньше, чемсоответственно. Каждое из предприятий, () может быть построено (или реконструировано) по одному из заранее подготовленных вариантов, причем вариантдля предприятияхарактеризуется следующими показателями:

• величины выпуска 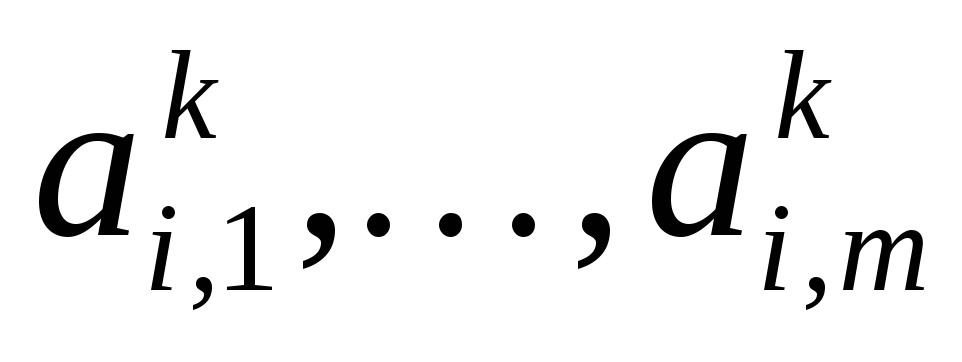по всем видам продукции;

• приведенные затраты .

Кроме того, имеются ресурсы , которые могут быть затрачены в количестве, не превышающем выделенногои затраты которых для вариантаравнысоответственно. Наконец, известно, что предприятия() обязательно должны войти в искомое решение, а предприятия- не обязательно.

Требуется с минимальными затратами и в пределах выделенных ресурсов удовлетворить потребность во всех видах продукции.

Вводя переменные , принимающие значения 1, если вариантреализуется, 0, если вариант не реализуется, запишем (целочисленную линейную) математическую модель.

Минимизировать функцию

, (1.7.)

при условиях

, , (1.8.)

, , (1.9.)

, , (1.10.)

, , (1.11.)

- целое, ,(1.13.)

Здесь (1.7.) – условие минимизации приведенных затрат. Из условий (1.10.), (1.11.), (1.12.), (1.13.) следует, что все переменные - булевы, т.е. принимают лишь значения 0 или 1. Условие (1.8.) соответствует удовлетворению всех потребностей, условие (1.9.) соответствует выполнению требования ограниченности запасов по всем ресурсам. Условие (1.10.) означает, что предприятияобязательно должны войти в искомое решение, а условие (1.11.) – что предприятия- не обязательно должны войти в искомое решение.

Особую роль играют здесь условия (1.10.) и (1.11.) – им соответствуют специальные упорядоченные множества (1-го типа ). При использовании метода ветвей и границ, ограничения этого типа учитываются алгоритмически, т.е. должны быть реализованы непосредственно в алгоритме решения задачи при использовании тех или иных эвристических правил.

При решении задач дискретной оптимизации возможен ряд упрощенных подходов:

• решение вместо задачи целочисленного линейного программирования (1.3.) – (1.6.) соответствующей задачи линейного программирования (1.3.) – (1.5.);

• полный перебор - например, в задаче коммивояжера;

• решение вместо задачи целочисленного линейного программирования (1.3.) – (1.6.) соответствующей задачи линейного программирования (1.3.) – (1.5.) с последующим «округлением» до приближенного целочисленного решения.

Первый способ в общем случае не гарантирует целочисленности. Второй способ не осуществим для задач сколько-нибудь значительных размеров. Третий способ может не только дать значительное отклонение от оптимума, но и вывести из области допустимых решений.

Тем не менее, эти упрощенные подходы содержат идеи основных методов решения задач дискретной оптимизации:

• метода отсечения;

• комбинаторных методов (методов ветвей и границ, методов неявного или направленного перебора);

• приближенных методов.

Метод отсечения основан на приспособлении хорошо разработанного аппарата линейного программирования для решения задач целочисленного линейного программирования. Исходный вариант идеи метода отсечения:

• в задаче (1.3.) – (1.6.) отбрасывается условие целочисленности (1.6.) и решается задача линейного программирования (1.3.) – (1.5.);

• если оптимальное решение задачи (1.3.) – (1.5.) удовлетворяет условию целочисленности (1.6.), то оно является решением исходной задачи (1.3.) – (1.6.);

• если оптимальное решение 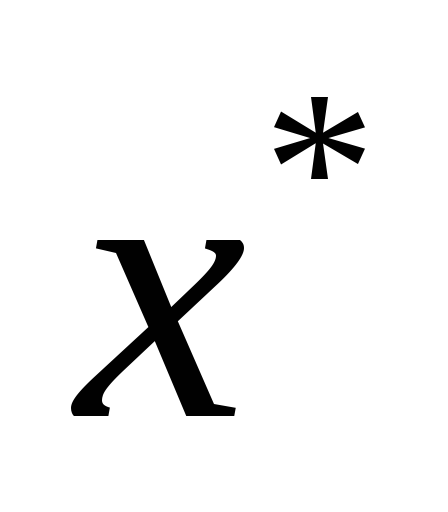задачи (1.3.) – (1.5.) не удовлетворяет условию целочисленности (1.6.), то вводится дополнительное линейное ограничение, которому заведомо удовлетворяют все допустимые решения задачи (1.3.) – (1.6.) и не удовлетворяет;

• гиперплоскость дополнительного линейного ограничения как бы «отсекает» 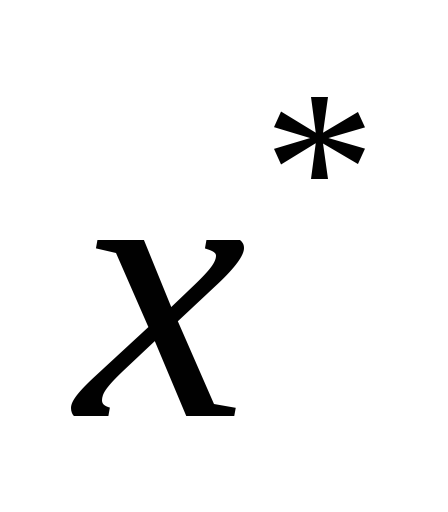от (целочисленных) допустимых решений задачи (1.3.) – (1.6.). Гиперплоскость присоединяется к условиям задачи (1.3.) – (1.6.):

• получается новая задача целочисленного программирования, к которой снова применяется тот же прием.

Имеются и другие способы применения аппарата линейного программирования к задачам целочисленного программирования (с использованием идеи отсечения). Во всех вариантах строятся дополнительные линейные ограничения, причем следует обеспечить конечность вычислительного процесса и принять меры против чрезмерного увеличения количества дополнительных линейных ограничений (что по-разному реализуется в разных алгоритмах).

Типичным представителем комбинаторных методов (методов неявного перебора) является наиболее распространенные методы ветвей и границ, идея которых проще всего поясняется на полностью () целочисленной задаче линейного программирования (1.3.) – (1.6.) с булевыми (,) переменными. Как и в методе отсечения, процесс решения начинается с решения исходной задачи линейного программирования (1.3.) – (1.5.). Если соответствующее оптимальное решениеудовлетворяет условию целочисленности (1.6.), то оно является и решением исходной задачи (1.3.) – (1.6.). Если же это не так, то по определенному правилу выбирается индекстакой, чтои производится ветвление на две подзадачи (1.3.) – (1.6.), (1.14’.) и (1.3.) – (1.6.), (1.14”.):

(1.14’.)

(1.14”.)

При этом заведомо:

• множество допустимых решений задачи (1.3.) – (1.6.) совпадает с объединением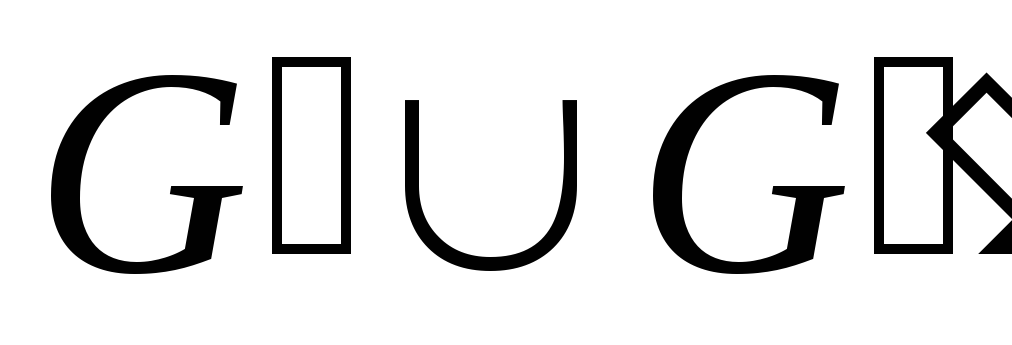множеств допустимых решений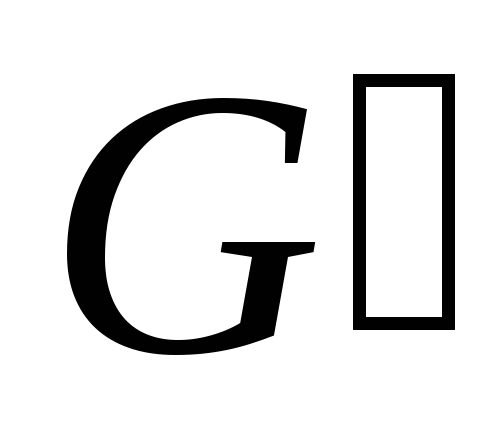(задача (1.3.) – (1.6.), (1.14’.)) и(задача (1.3.) – (1.6.), (1.14”.));

• если - допустимое решение задачи (1.3.) – (1.6.),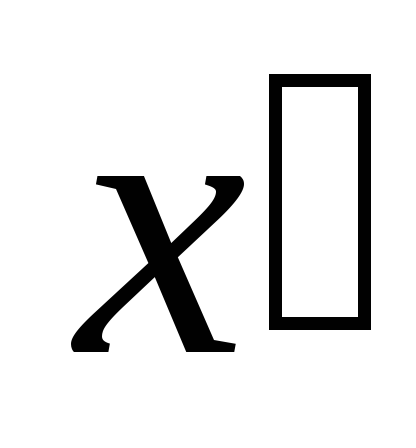- оптимальное решение задачи (1.3.) – (1.6.), (1.14’.),- оптимальное решение задачи (1.3.) – (1.6.), (1.14”.) (для задачи на максимум), то.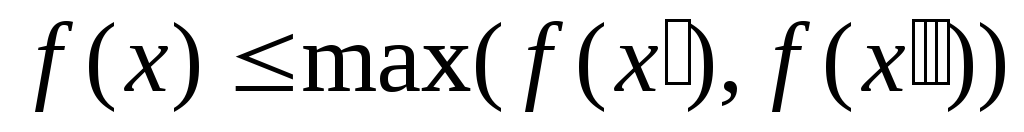

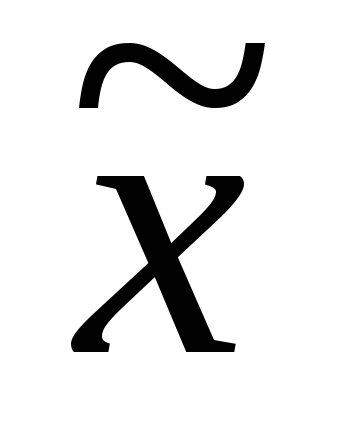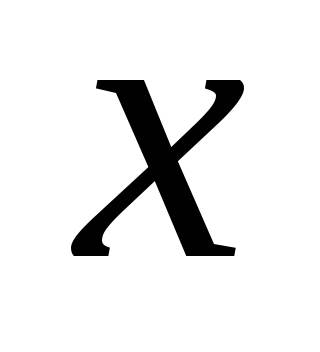• если - искомое оптимальное решение задачи (1.3.) – (1.6.),- допустимое решение задачи (1.3.) – (1.6.), то.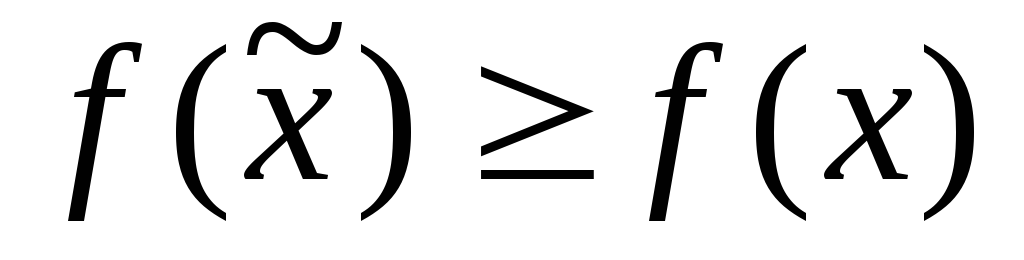

Эти простые соображения позволяют построить конечный метод точного решения задачи (1.3.) – (1.6.), на базе которого легко строится его приближенная модификация.

Многие из приближенных методов основаны на использовании случайного поиска (или случайного поиска с локальной оптимизацией). Предложены и детерминированные приближенные методы, использующие специфику различных задач и различные эвристические приемы. Некоторые из приближенных методов основаны на том или ином из точных методов (например, на методах ветвей и границ), что не исключает использование в них ряда эвристических правил.

Основные направления развития методов дискретной оптимизации:

• методы направленного перебора;

• приближенные методы;

• комбинированные (гибридные) методы, основанные на сочетании различных подходов;

• методы решения специальных задач.