9. Особенности метода решения распределительной задачи

Особенность матрицы условий распределительной задачи заключается в том, что в каждом ее столбце всего два ненулевых элемента. На этом основаны специальные методы решения распределительной задачи. Принципы построения подобных методов могут быть распространены для решения других задач с матрицами условий, содержащими в каждой строке не более двух ненулевых элементов. Одна из таких задач рассмотрена ниже.

Пусть требуется составить наиболее экономный план построения геодезической сети. Расходы по строительству сети определяются, главным образом, высотами геодезических вышек и издержками на подвоз материалов к месту строительства. Предполагается, что пункты строительства намечены и задача состоит в выборе выбор вышек, обеспечивающих соблюдение условий видимости при заданном рельефе местности.

Пусть - высота препятствия между вышкамии, аи- расстояние до препятствия соответственно от вышеки пусть, кроме того,

.

В этих обозначениях условия видимости вышки с вышкизаписываются в виде (рис. 9.1.)

. (9.1.)

Неравенство (9.1.) должно иметь место для всех , соответствующих парам вышек, для которых требуется прямая видимость.

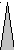
Рис. 9.1. Схема расположения вышек и.

Издержки на строительство вышки высотой характеризуются нелинейной, выпуклой вниз функцией, так как издержки растут быстрее, чем увеличивается высота вышки

.

Коэффициенты зависят от транспортных издержек на подвоз материалов к месту строительства вышки.

Таким образом, составление плана построения геодезической сети сводится к вычислению высот , для которых достигает максимума функция

(9.2)

при выполнении условий

(9.3)

, (9.4.)

где - выпуклые вниз функции;

- множество пар индексов (), отвечающим номерам вышек, между которыми должна быть обеспечена прямая видимость;

- сегмент определяющий допустимый диапазон изменения высоты вышки .

Выпуклые вниз функции могут быть с любой заранее заданной степенью точности приближены ломанными линиями. Отсюда возможность замены нелинейной задачи (9.2.) – (9.4.) специальной задачей линейного программирования. При этом уравнения прямых, которым принадлежат звенья ломанной, записываются в виде

(9.5.)

где

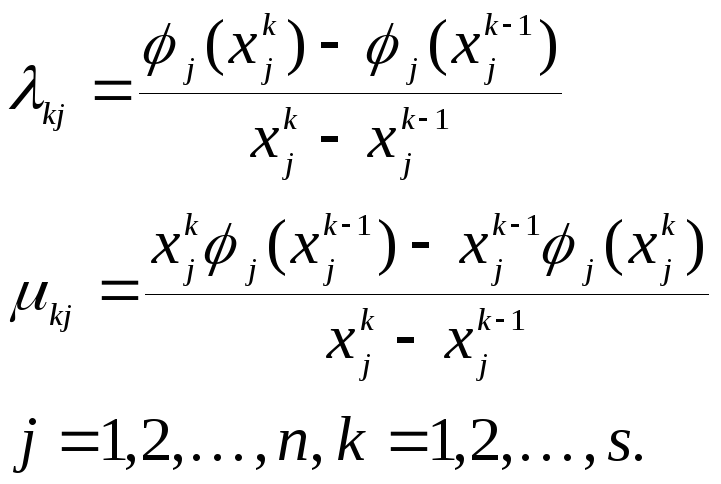(9.6.)

Тогда задача вычисления при условиях (9.3.) – (9.4.) может быть с любой степенью точности заменена задачей вычисленияпри тех же условиях, где. Последняя задача может быть решена методами линейного программирования.

10. Задачи с разрывной целевой функцией

Из задач этого типа наиболее важной и изученной является так называемая транспортная задача с фиксированными доплатами. Пусть, как в обычной транспортной задаче, через обозначены пункты производства некоторого однородного груза, через- пункты его потребления. Даны величины:

- объем производства в пункте производства ;

- объем потребления в пункте потребления .

Требуется найти объемы перевозок из пунктав пункт, удовлетворяющие естественным транспортным ограничениям

, ,,,, (10.1.)

и минимизирующие функцию

. (10.2)

Каждое в (10.2.) имеет вид

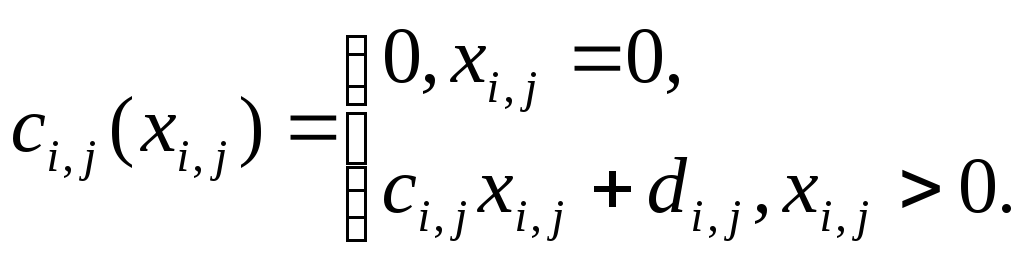(10.3.)

Величины естественно интерпретировать как затраты на перевозку единицы груза изв. Подможно подразумевать , например, плату за аренду транспортных средств, не зависящую от их загрузки, либо затраты на строительство магистрали от каждого пунктадо каждого пункта, не зависящие от будущих грузопотоков. Естественно считать всеинеотрицательными.

Задачу (10.1.) – (10.3.) называют транспортной задачей с фиксированными доплатами, или неоднородной транспортной задачей. Если все , задача превращается в обычную транспортную. В противном случае эта задача из-за разрывности каждого слагаемого (10.3.) в нуле вообще выпадает из рамок линейного программирования. Однако, если ввести дополнительные целочисленные переменные, задача сводится к частично целочисленной задаче линейного программирования.

Способ такого сведения был указан Балинским и состоит в следующем. Найдем величины

, ,. (10.4.)

Рассмотрим задачу минимизации

(10.5.)

при условиях (10.1.) и дополнительном условии

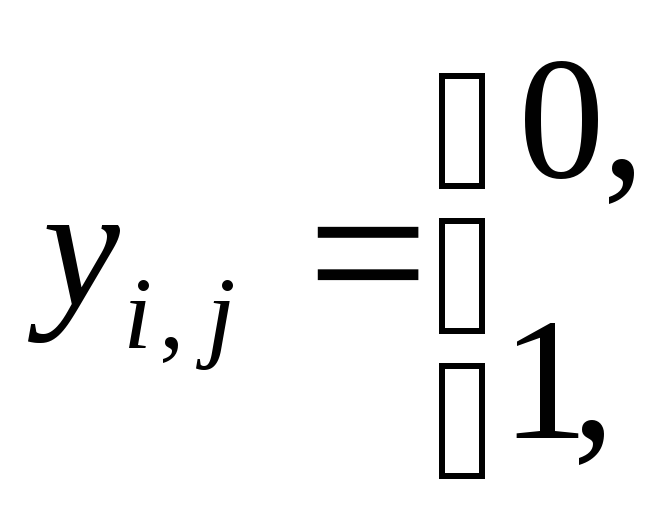
. (10.6.)

Частично целочисленная задача (10.5.), (10.1.), (10.6.) оказывается эквивалентной исходной задаче (10.1.) – (10.3.). Действительно, при в силу (10.6.) автоматически будет и, а принеравенства (10.6.) становятся излишними, так как при любом допустимом плане транспортной задачи условиявыполнены всегда. Наоборот, если в некотором оптимальном плане задачи (10.5.), (10.1.), (10.6.) будет, то соответствующее значениедолжно быть нулем. Если оно окажется положительным, то план не будет оптимальным, ибо, уменьшив это значение, не нарушим ограничений и придадим целевой функции (10.5.) меньшее значение. Наконец, если, то в силу условий (10.6.)может быть только единицей.

Таким образом, целочисленные переменные в этой постановке согласуют строительство магистралей между пунктамии(или в зависимости от интерпретации, аренду транспорта для этой магистрали) и осуществление перевозок междуи.

Основанный на этом приближенный метод решения транспортной задачи с фиксированными доплатами базируется на двух теоремах.

Теорема 1.

Если в транспортной задаче с фиксированными доплатами все и соответствующая ей обычная транспортная задача (без доплат) с матрицейне вырождена, то оптимальные планы для задач с доплатами и без доплат совпадают.

Оптимальные значения целевых функций в этом случае будут отличаться на , и уменьшить это значение невозможно.

Теорема 2.

Если в задаче с доплатами различны, то ее оптимальный план следует искать среди опорных планов соответствующей ей транспортной задачи (без доплат) с матрицей.

Это утверждение становится ясным, если учесть, что целевая функция, будучи суммой вогнутых функций, сама является вогнутой. Следовательно, ее экстремумы будут достигаться в крайних точках многогранного выпуклого множества.

Поскольку речь идет о минимизации вогнутой функции, любой стандартный метод даст, вообще говоря, лишь локальный, а не глобальный минимум.

Рассмотрим более общую модель с неоднородной разрывной целевой функцией. Ее удобно сформулировать в терминах задачи о смесях, хотя такая интерпретация не является единственно возможной. Обозначим через компоненты смеси, а через- интересующие элементы в этих компонентах. Заданы следующие величины:

- содержание элемента в единице компоненты,

- ограничения снизу на содержание каждого элемента в смеси,

- стоимость закупки единицы компоненты ,

- фиксированная стоимость заказа компоненты , не зависящая от заказываемого количества.

Требуется составить наиболее дешевую смесь, удовлетворяющую заданным ограничениям. Обозначим искомые количества компонент через . Тогда задача сведется к минимизации

(10.7.)

при условиях

, ,, (10.8.)

где

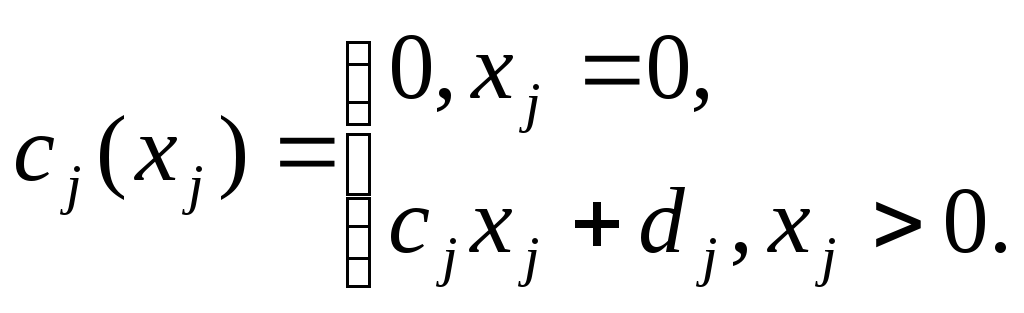(10.9.)

Следует отметить, что требование целочисленности на переменные не накладывается.

Эту задачу можно свести к общей частично целочисленной задаче линейного программирования с помощью приема, представленного выше. Предположим, что в дополнение к условиям (10.8.) заданы еще верхние границы для переменных:

, (10.10.)

(или эти границы могут быть определены из экономической сущности задачи хотя бы грубым образом). Рассмотрим задачу минимизации

(10.11.)

при условиях (10.8.) и дополнительном условии

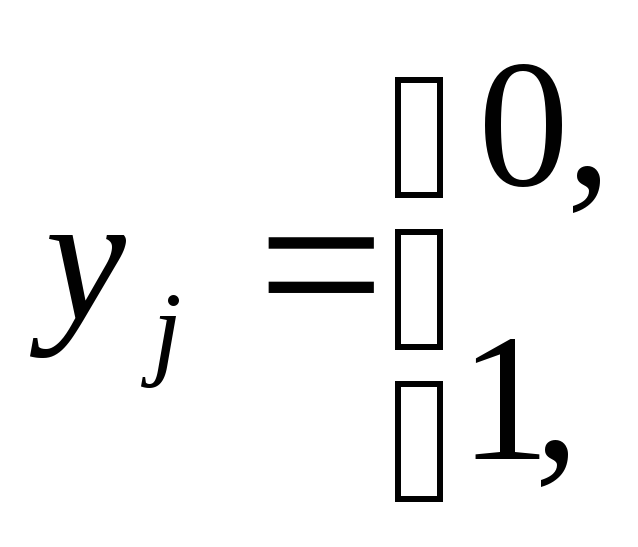
. (10.12.)

Эквивалентность частично целочисленной задачи (10.11.), (10.8.), (10.12.) и исходной задачи устанавливается аналогичным способом приведенным выше.

Отметим, что возможность сведения задач с разрывной целевой функцией к частично целочисленным базируется на наличии верхних границ для переменных. Этот прием вообще является характерным для целочисленного программирования. В транспортной задаче эти границы определяются внутренним образом. В общей задаче их нужно постулировать или определять особым образом. В некоторых случаях границы вычисляются просто. Например, если все , то в качествеможно взять

, , (10.13.)

где минимум берется по всем , для которых.